1.4.2 二次函数的应用(围篱笆问题)(含解析)
文档属性
| 名称 | 1.4.2 二次函数的应用(围篱笆问题)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:05:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
二次函数应用(围篱笆问题)
一、单选题
1.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为ym2,则y关于x的函数表达式为( )
A.y=- x2+26x(2≤x<52) B.y=- x2+50x(2≤x<52)
C.y=-x2+52x(2≤x<52) D.y=- x2+27x-52(2≤x<52)
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
3.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y ,则y关于x的函数表达式为( )
A.y=﹣ x2+26x(2≤x<52) B.y=﹣ x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52) D.y=﹣ x2+27x﹣52(2≤x<52)
二、填空题
4.长方形的周长为24厘米,其中一边为x(其中),面积为y平方厘米,则这样的长方形中y与x的关系可以写为
5.如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF。若四边形AECF是矩形,则矩形AEGF的面积y关于BE的长工的函数解析式是 (不用写出x的取值范围)
三、解答题
6.在美化校园的活动中,某兴趣小组用总长为28米的围栏材料,一面靠墙,围成一个矩形花园,墙长8米,设AB的长为x米,矩形花园的面积为S平方米,当x为多少时,S取得最大值,最大值是多少?
7.如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
(1)写出S与x之间的函数表达式,并写出x的取值范围.
(2)当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?
8.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米.
(1)请直接写出y关于x的函数解析式.(不必写出x的取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
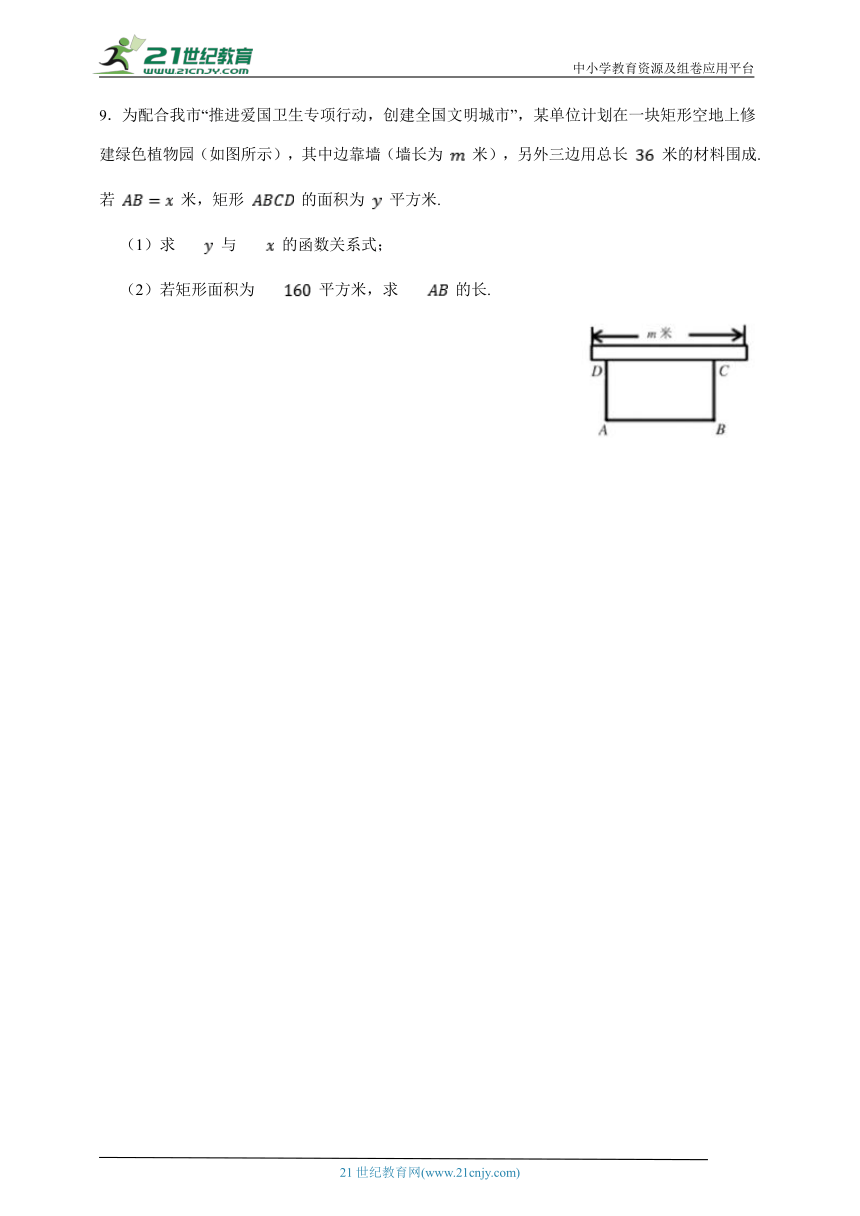
9.为配合我市“推进爱国卫生专项行动,创建全国文明城市”,某单位计划在一块矩形空地上修建绿色植物园(如图所示),其中边靠墙(墙长为 米),另外三边用总长 米的材料围成.若 米,矩形 的面积为 平方米.
(1)求 与 的函数关系式;
(2)若矩形面积为 平方米,求 的长.
答案解析部分
1.【答案】A
【解析】【解答】解:∵ 栅栏总长度为50m, 饲养室长为xm, 门宽为2m,
∴ 饲养室宽为()m,
∴y=()x=(2≤x<52).
故答案为:A.
【分析】根据题意求出饲养室的宽,利用矩形的面积公式列出式子进行化简,即可得出答案.
2.【答案】B
【解析】【解答】解:设垂直于墙的一边的长为xm,隔离区的面积为ym2,
∴y=x(12-x)=-3(x-2)2+12,
∵12-3x≤5,
∴x≥,
∵抛物线的对称轴为直线x=2,开口向下,
∴当x=时,y有最大值为,
故小明错误,
当x=3时,y=9,
故小亮正确.
故答案为:B.
【分析】设垂直于墙的一边的长为xm,隔离区的面积为ym2,根据题意得出y=-3(x-2)2+12,x≥,根据二次函数的性质得出当x=时,y有最大值为,即可判断小明错误,当x=3时,y=9,即可判断小亮正确.
3.【答案】A
【解析】【解答】解:y关于x的函数表达式为:y (50+2﹣x)x
x2+26x(2≤x<52).
故答案为:A.
【分析】饲养场的长为xm,则宽为(50+2-x)m,由矩形的面积y=矩形的长×宽可求解.
4.【答案】y=
【解析】【解答】解:长方形的一边是xcm,则另一边长是(12-x)cm.
则y=(12-x)x=-x2+12x.
故答案是:y=
【分析】根据长方形的面积=长×宽即可求解.
5.【答案】y=16-x2
【解析】【解答】解:∵ 正方形ABCD的边长是4,
∴AB=AD=4,
∵ BE=DF =x,
∴AE=4-x,AF=4+x,
∴ 矩形AEGF的面积y=AE·AF=(4-x)(4+x)=16-x2.
【分析】根据题意求出AE=4-x,AF=4+x,再根据矩形的面积公式得出y=AE·AF,再进行化简,即可得出答案.
6.【答案】解: .
,
当 时,S有最大值,最大值
【解析】【分析】由题意可得出: ,再利用二次函数增减性求得最值
7.【答案】(1)解:∵AB=CD=xm,∴BC=(80﹣2x)m,
∴S=x(80﹣2x)=﹣2x2+80x,
∴ ,
∴ ,
∴ ,
∴15≤x<40
∴S=﹣2x2+80x,(15≤x<40)
(2)解:∵S=﹣2(x2﹣40x+400﹣400)=﹣2(x﹣20)2+800,
∵15≤x<40,
∴当x=20时,S有最大值为800,
∴即当AB=20m,BC=40m时,面积S有最大值为800m2
【解析】【分析】(1)易得BC=(80-2x)m,然后根据矩形的面积公式可得S,根据AB>0、0(2)对S进行配方,然后结合二次函数的性质以及x的范围进行解答.
8.【答案】(1)y =2 x2 -42x +160
(2)解:依题意,得 2 x2 -42x +160=120 ,
整理,得 x 2 -21 x +20=0 ,
解得 x 1 =1 , x 2 =20.
当 x =1 时, 10-2 x =8>0 ,符合题意 .
当 x =20 时, 10-2 x =-30<0 ,不符合题意,舍去 .
答:竖甬道的宽度为 1 米
【解析】【解答】解:(1)横甬道的宽度为 2 x 米,剩余部分可合成长( 16- x )米,宽( 10-2 x )米的矩形 .依题意,得 y = ( 16- x )( 10-2 x ) =2 x 2 -42 x +160.
【分析】(1)根据题意得出横甬道的宽度为2x米,剩余部分合成长为(16- x )米,宽为( 10-2x )米的矩形,利用矩形的面积公式得出y=(16- x )(10- 2x ),进行化简即可得出答案;
(2)根据题意列出方程,解方程求出x的值,再进行检验,即可得出答案.
9.【答案】(1)解:由题意
即 ;
(2)解:由(1)知: ,即
,
解得 , ,
答: 的长为 米或20米.
【解析】【分析】(1)根据三边总长36米,表示出AD的长为 ,然后根据矩形面积公式即可列出y和x的关系式;(2)令(1)中y=160,解出对应x值即可;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
二次函数应用(围篱笆问题)
一、单选题
1.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为ym2,则y关于x的函数表达式为( )
A.y=- x2+26x(2≤x<52) B.y=- x2+50x(2≤x<52)
C.y=-x2+52x(2≤x<52) D.y=- x2+27x-52(2≤x<52)
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
3.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y ,则y关于x的函数表达式为( )
A.y=﹣ x2+26x(2≤x<52) B.y=﹣ x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52) D.y=﹣ x2+27x﹣52(2≤x<52)
二、填空题
4.长方形的周长为24厘米,其中一边为x(其中),面积为y平方厘米,则这样的长方形中y与x的关系可以写为
5.如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF。若四边形AECF是矩形,则矩形AEGF的面积y关于BE的长工的函数解析式是 (不用写出x的取值范围)
三、解答题
6.在美化校园的活动中,某兴趣小组用总长为28米的围栏材料,一面靠墙,围成一个矩形花园,墙长8米,设AB的长为x米,矩形花园的面积为S平方米,当x为多少时,S取得最大值,最大值是多少?
7.如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
(1)写出S与x之间的函数表达式,并写出x的取值范围.
(2)当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?
8.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米.
(1)请直接写出y关于x的函数解析式.(不必写出x的取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
9.为配合我市“推进爱国卫生专项行动,创建全国文明城市”,某单位计划在一块矩形空地上修建绿色植物园(如图所示),其中边靠墙(墙长为 米),另外三边用总长 米的材料围成.若 米,矩形 的面积为 平方米.
(1)求 与 的函数关系式;
(2)若矩形面积为 平方米,求 的长.
答案解析部分
1.【答案】A
【解析】【解答】解:∵ 栅栏总长度为50m, 饲养室长为xm, 门宽为2m,
∴ 饲养室宽为()m,
∴y=()x=(2≤x<52).
故答案为:A.
【分析】根据题意求出饲养室的宽,利用矩形的面积公式列出式子进行化简,即可得出答案.
2.【答案】B
【解析】【解答】解:设垂直于墙的一边的长为xm,隔离区的面积为ym2,
∴y=x(12-x)=-3(x-2)2+12,
∵12-3x≤5,
∴x≥,
∵抛物线的对称轴为直线x=2,开口向下,
∴当x=时,y有最大值为,
故小明错误,
当x=3时,y=9,
故小亮正确.
故答案为:B.
【分析】设垂直于墙的一边的长为xm,隔离区的面积为ym2,根据题意得出y=-3(x-2)2+12,x≥,根据二次函数的性质得出当x=时,y有最大值为,即可判断小明错误,当x=3时,y=9,即可判断小亮正确.
3.【答案】A
【解析】【解答】解:y关于x的函数表达式为:y (50+2﹣x)x
x2+26x(2≤x<52).
故答案为:A.
【分析】饲养场的长为xm,则宽为(50+2-x)m,由矩形的面积y=矩形的长×宽可求解.
4.【答案】y=
【解析】【解答】解:长方形的一边是xcm,则另一边长是(12-x)cm.
则y=(12-x)x=-x2+12x.
故答案是:y=
【分析】根据长方形的面积=长×宽即可求解.
5.【答案】y=16-x2
【解析】【解答】解:∵ 正方形ABCD的边长是4,
∴AB=AD=4,
∵ BE=DF =x,
∴AE=4-x,AF=4+x,
∴ 矩形AEGF的面积y=AE·AF=(4-x)(4+x)=16-x2.
【分析】根据题意求出AE=4-x,AF=4+x,再根据矩形的面积公式得出y=AE·AF,再进行化简,即可得出答案.
6.【答案】解: .
,
当 时,S有最大值,最大值
【解析】【分析】由题意可得出: ,再利用二次函数增减性求得最值
7.【答案】(1)解:∵AB=CD=xm,∴BC=(80﹣2x)m,
∴S=x(80﹣2x)=﹣2x2+80x,
∴ ,
∴ ,
∴ ,
∴15≤x<40
∴S=﹣2x2+80x,(15≤x<40)
(2)解:∵S=﹣2(x2﹣40x+400﹣400)=﹣2(x﹣20)2+800,
∵15≤x<40,
∴当x=20时,S有最大值为800,
∴即当AB=20m,BC=40m时,面积S有最大值为800m2
【解析】【分析】(1)易得BC=(80-2x)m,然后根据矩形的面积公式可得S,根据AB>0、0
8.【答案】(1)y =2 x2 -42x +160
(2)解:依题意,得 2 x2 -42x +160=120 ,
整理,得 x 2 -21 x +20=0 ,
解得 x 1 =1 , x 2 =20.
当 x =1 时, 10-2 x =8>0 ,符合题意 .
当 x =20 时, 10-2 x =-30<0 ,不符合题意,舍去 .
答:竖甬道的宽度为 1 米
【解析】【解答】解:(1)横甬道的宽度为 2 x 米,剩余部分可合成长( 16- x )米,宽( 10-2 x )米的矩形 .依题意,得 y = ( 16- x )( 10-2 x ) =2 x 2 -42 x +160.
【分析】(1)根据题意得出横甬道的宽度为2x米,剩余部分合成长为(16- x )米,宽为( 10-2x )米的矩形,利用矩形的面积公式得出y=(16- x )(10- 2x ),进行化简即可得出答案;
(2)根据题意列出方程,解方程求出x的值,再进行检验,即可得出答案.
9.【答案】(1)解:由题意
即 ;
(2)解:由(1)知: ,即
,
解得 , ,
答: 的长为 米或20米.
【解析】【分析】(1)根据三边总长36米,表示出AD的长为 ,然后根据矩形面积公式即可列出y和x的关系式;(2)令(1)中y=160,解出对应x值即可;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
