浙教版九年级上册3.3 垂径定理课件(共16张PPT)
文档属性
| 名称 | 浙教版九年级上册3.3 垂径定理课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 287.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 17:03:38 | ||
图片预览


文档简介
(共16张PPT)
初三数学新授课
3.3 垂径定理(1)
(A层)
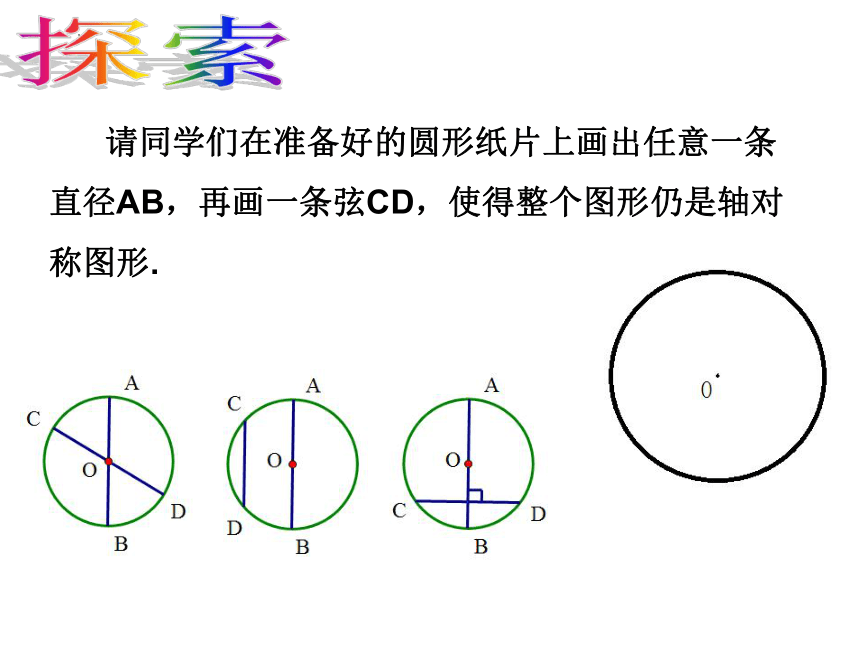
请同学们在准备好的圆形纸片上画出任意一条直径AB,再画一条弦CD,使得整个图形仍是轴对称图形.
探索
(1)在圆纸片上任意作一条直径AB
能够重合的弧叫等弧
分一条弧成相等的两条弧的点
叫这条弧的中点
(2)作弦CD垂直于AB,垂足为P,
将纸片沿着直径AB对折,你发现哪些点、线段、圆弧重合?
探索
理由如下:∵∠OPC=∠OPD=Rt∠,
根据圆的轴对称性,可得射线PC与PD重合,
∴点C与点D重合,弧AC和弧AD重合,弧BC和弧BD重合.
∴ PC=PD, AC= AD, BC=BD.
⌒
⌒
⌒
⌒
垂径定理:
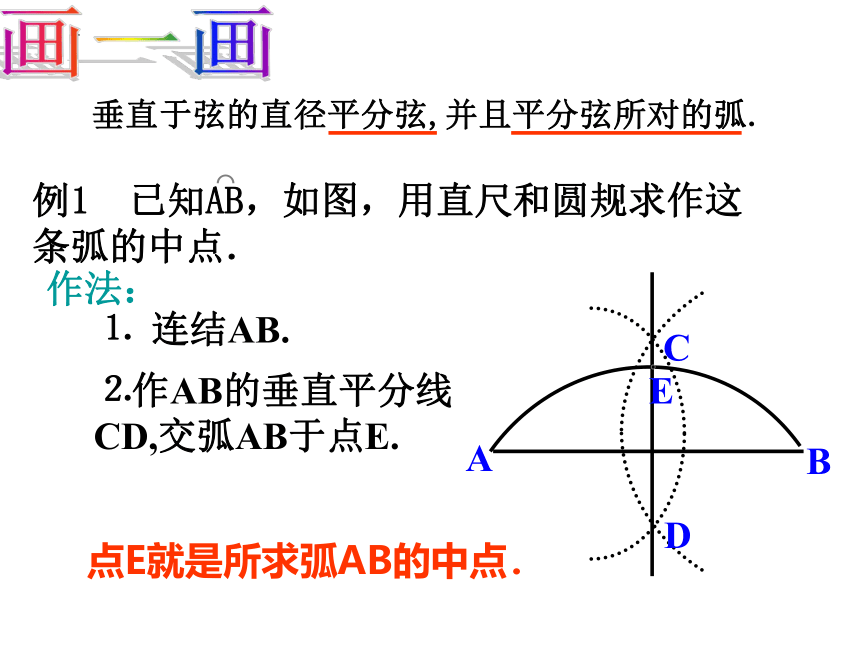
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
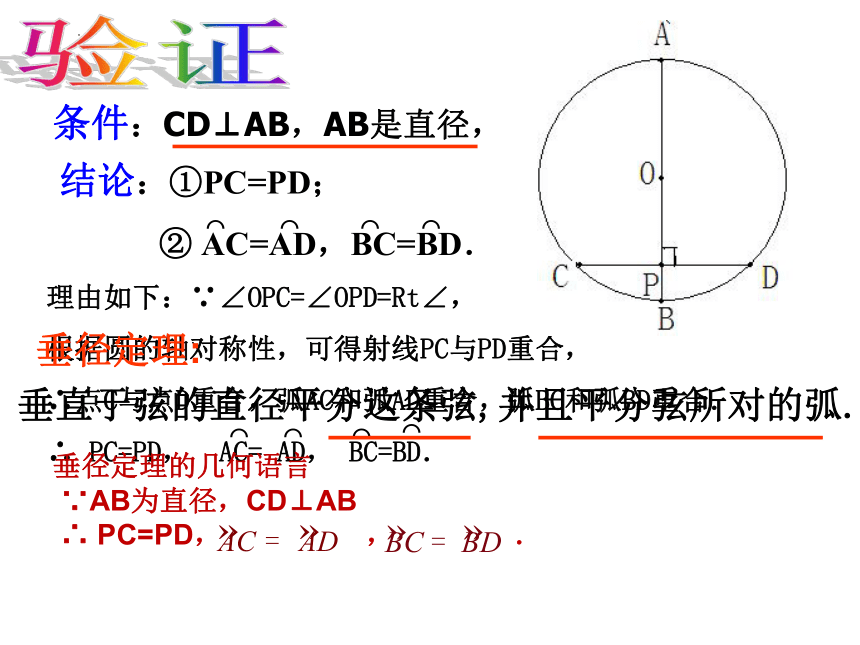
条件:CD⊥AB,AB是直径,
结论:①PC=PD;
② AC=AD,BC=BD.
⌒
⌒
⌒
⌒
验证
垂径定理的几何语言
∵AB为直径,CD⊥AB
∴ PC=PD, , .
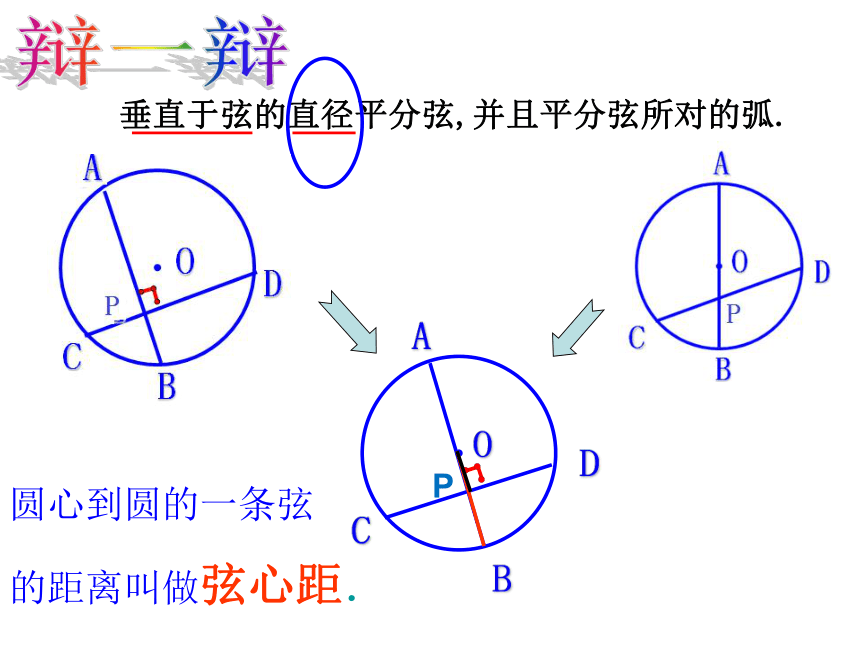
垂直于弦的直径平分弦,并且平分弦所对的弧.
O
C
D
A
B
圆心到圆的一条弦
的距离叫做弦心距.
P
辩一辩
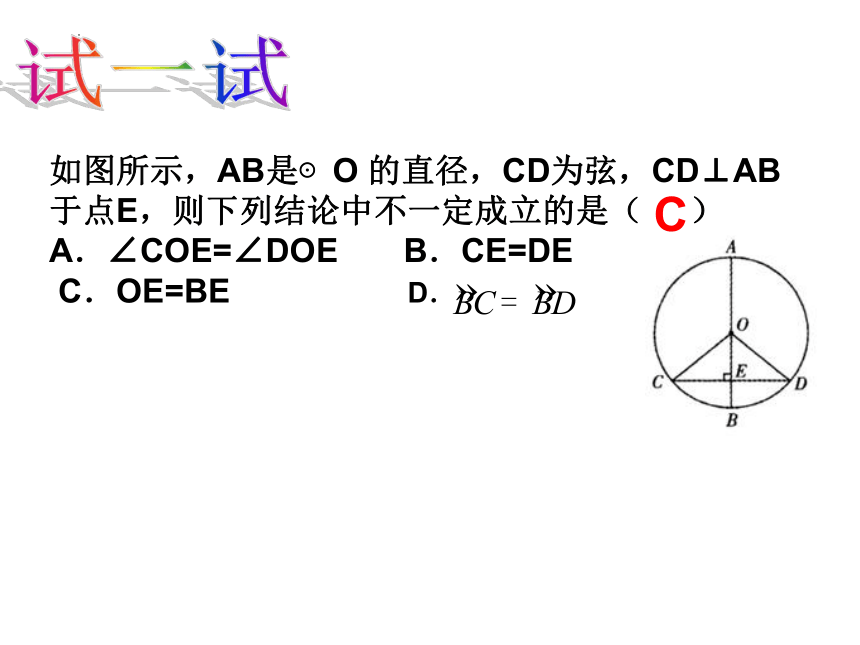
如图所示,AB是⊙O 的直径,CD为弦,CD⊥AB于点E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
试一试
C
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
C
D
A
B
E
例1 已知AB,如图,用直尺和圆规求作这条弧的中点.
⌒
垂直于弦的直径平分弦,并且平分弦所对的弧.
画一画
变一变: 求弧AB的四等分点.
C
D
A
B
E
F
G
m
n
例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,求截面圆心O到水面的距离OC .
弦心距(d)
半弦
C
半径(r)
变一变 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,求截面中水的最大深度.
C
变式 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,当水面宽由AB上升到EF=16时,求水面上升的高度 .
举一反三
举一反三
1、如图,圆O中弦AB的长为8,半径OD ⊥ AB于点C,DC=2,求圆O的半径.
变式1 如图,圆O中弦AB的长为8,CE过圆心O且垂直AB于点C,CE=8,求圆O的半径.
C
D
E
某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直评分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是多少?
应用
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
(1)画弦心距和半径是圆中常见的辅助线;
回顾小结
4.思想方法:
(1)方程思想
(2)建模思想
变式2 已知圆O的直径为10,弦AB,CD互相垂直,交于点E,且AE=2,BE=6,求CE,DE的长度.
变式3 如图,圆内一弦CD与直径AB相交成30 °,且分直径为1cm和5cm,则圆心到这条弦的距离为多少?CD长为多少?
举一反三
1.如图,已知∠C=90 °, ⊙C与AB相交于点D,AC=5,CB=12,求AD的长.
课后拓展
2.如图,在△ABC中,∠C=90°,AC= ,BC=5,以C为圆心、BC为半径作圆交BA的延长线于点D,则AD的长为
课后拓展
设未知数,利用两直角三角形的公共边,由勾股定理建立相等关系.
初三数学新授课
3.3 垂径定理(1)
(A层)
请同学们在准备好的圆形纸片上画出任意一条直径AB,再画一条弦CD,使得整个图形仍是轴对称图形.
探索
(1)在圆纸片上任意作一条直径AB
能够重合的弧叫等弧
分一条弧成相等的两条弧的点
叫这条弧的中点
(2)作弦CD垂直于AB,垂足为P,
将纸片沿着直径AB对折,你发现哪些点、线段、圆弧重合?
探索
理由如下:∵∠OPC=∠OPD=Rt∠,
根据圆的轴对称性,可得射线PC与PD重合,
∴点C与点D重合,弧AC和弧AD重合,弧BC和弧BD重合.
∴ PC=PD, AC= AD, BC=BD.
⌒
⌒
⌒
⌒
垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
条件:CD⊥AB,AB是直径,
结论:①PC=PD;
② AC=AD,BC=BD.
⌒
⌒
⌒
⌒
验证
垂径定理的几何语言
∵AB为直径,CD⊥AB
∴ PC=PD, , .
垂直于弦的直径平分弦,并且平分弦所对的弧.
O
C
D
A
B
圆心到圆的一条弦
的距离叫做弦心距.
P
辩一辩
如图所示,AB是⊙O 的直径,CD为弦,CD⊥AB于点E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
试一试
C
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
C
D
A
B
E
例1 已知AB,如图,用直尺和圆规求作这条弧的中点.
⌒
垂直于弦的直径平分弦,并且平分弦所对的弧.
画一画
变一变: 求弧AB的四等分点.
C
D
A
B
E
F
G
m
n
例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,求截面圆心O到水面的距离OC .
弦心距(d)
半弦
C
半径(r)
变一变 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,求截面中水的最大深度.
C
变式 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=12,当水面宽由AB上升到EF=16时,求水面上升的高度 .
举一反三
举一反三
1、如图,圆O中弦AB的长为8,半径OD ⊥ AB于点C,DC=2,求圆O的半径.
变式1 如图,圆O中弦AB的长为8,CE过圆心O且垂直AB于点C,CE=8,求圆O的半径.
C
D
E
某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直评分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是多少?
应用
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:
(1)画弦心距和半径是圆中常见的辅助线;
回顾小结
4.思想方法:
(1)方程思想
(2)建模思想
变式2 已知圆O的直径为10,弦AB,CD互相垂直,交于点E,且AE=2,BE=6,求CE,DE的长度.
变式3 如图,圆内一弦CD与直径AB相交成30 °,且分直径为1cm和5cm,则圆心到这条弦的距离为多少?CD长为多少?
举一反三
1.如图,已知∠C=90 °, ⊙C与AB相交于点D,AC=5,CB=12,求AD的长.
课后拓展
2.如图,在△ABC中,∠C=90°,AC= ,BC=5,以C为圆心、BC为半径作圆交BA的延长线于点D,则AD的长为
课后拓展
设未知数,利用两直角三角形的公共边,由勾股定理建立相等关系.
同课章节目录
