2022-2023学年浙教版八年级数学上册1.5三角形全等的判定同步练习题(Word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册1.5三角形全等的判定同步练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 11:30:37 | ||
图片预览



文档简介
2022-2023学年浙教版八年级数学上册《1.5三角形全等的判定》同步练习题(附答案)
一.选择题
1.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,H是△ABC的高AD、BE的交点,且AD=BE,则下列结论中正确的有①AE=BD,②AH=BH,③EH=DH,④∠HAB=∠HBA( )
A.1个 B.2个 C.3个 D.4个
4.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
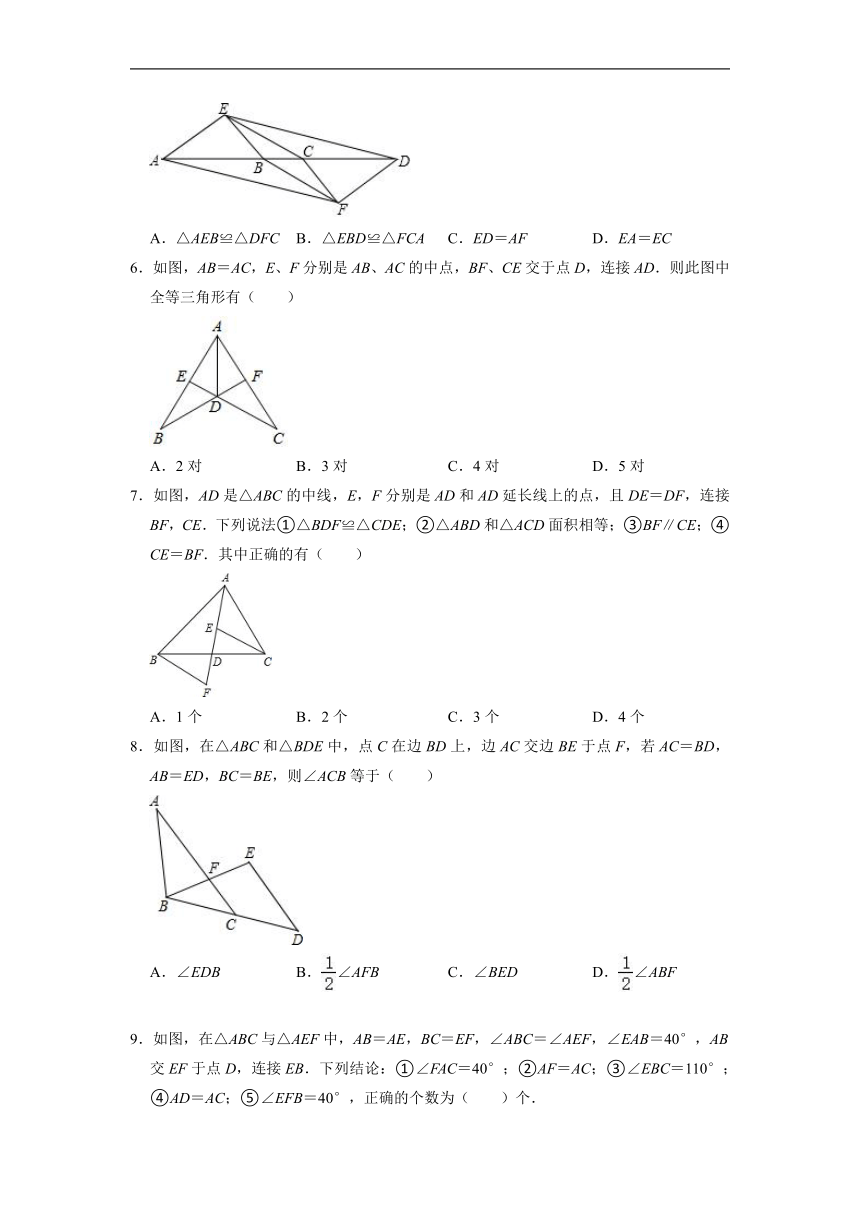
5.如图,已知AE∥DF,BE∥CF,AC=BD,则下列说法错误的是( )
A.△AEB≌△DFC B.△EBD≌△FCA C.ED=AF D.EA=EC
6.如图,AB=AC,E、F分别是AB、AC的中点,BF、CE交于点D,连接AD.则此图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
7.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠AFB C.∠BED D.∠ABF
9.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°,正确的个数为( )个.
A.1 B.2 C.3 D.4
10.如图,已知△ABC≌△AEF,其中AB=AE,∠B=∠E.在下列结论①AC=AF,②∠BAF=∠B,③EF=BC,④∠BAE=∠CAF中,正确的个数有( )
A.1个 B.2个 C.3个 D.4个
11.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.
A.1 B.2 C.3 D.4
13.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
二.填空题
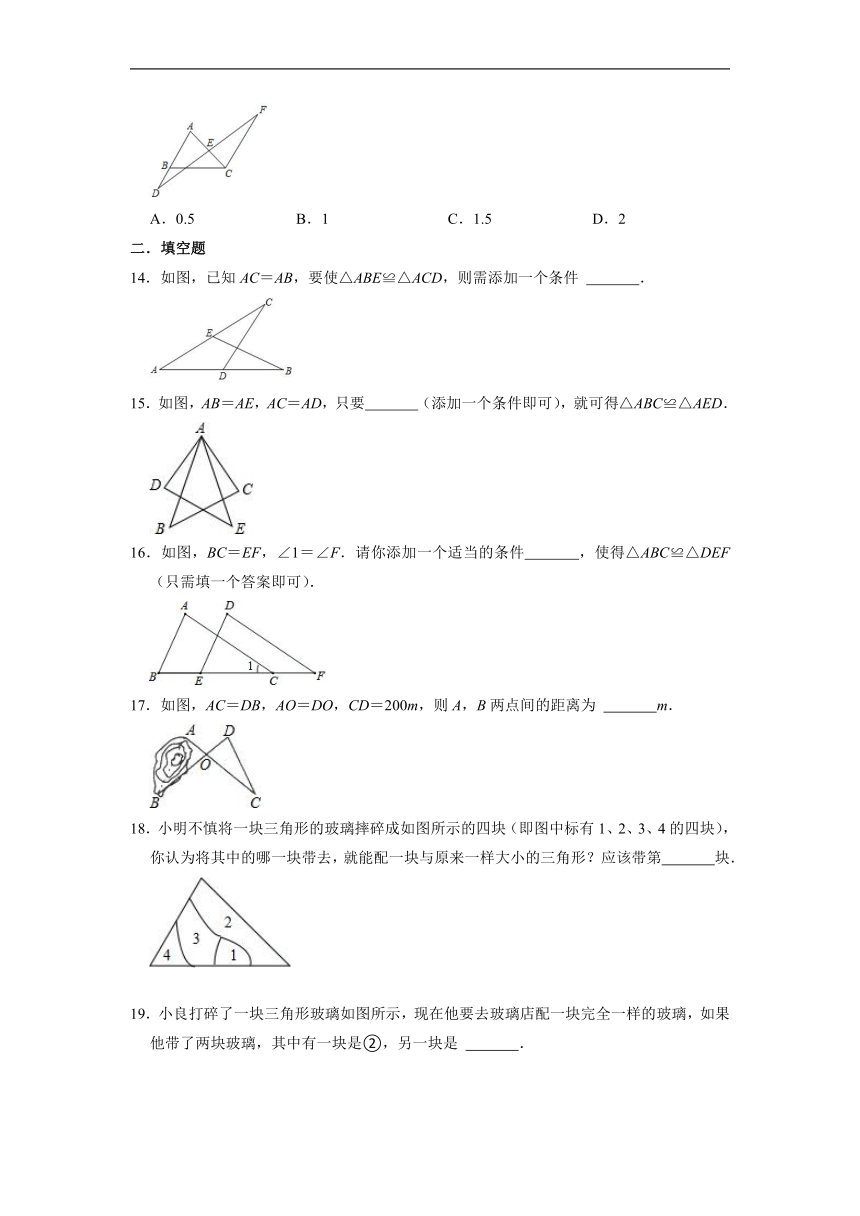
14.如图,已知AC=AB,要使△ABE≌△ACD,则需添加一个条件 .
15.如图,AB=AE,AC=AD,只要 (添加一个条件即可),就可得△ABC≌△AED.
16.如图,BC=EF,∠1=∠F.请你添加一个适当的条件 ,使得△ABC≌△DEF(只需填一个答案即可).
17.如图,AC=DB,AO=DO,CD=200m,则A,B两点间的距离为 m.
18.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
19.小良打碎了一块三角形玻璃如图所示,现在他要去玻璃店配一块完全一样的玻璃,如果他带了两块玻璃,其中有一块是②,另一块是 .
20.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=65°,∠ACB=35°,然后在M处立了标杆,使∠MBC=65°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里得到△MBC≌△ABC的依据是 .
三.解答题
21.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,点 A、E、B、D在同一直线上,BC、EF交于点M,AC=DF,AB=DE.
求证:(1)∠CBA=∠FED;
(2)AM=DM.
22.如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE;
(2)若∠BAE=125°,求∠DCB的度数.
23.如图所示,BD、CE是△ABC高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)判断:∠1 ∠2(用“>”、“<”、“=”填空);
(2)探究:PA与AQ之间的关系;
(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究PA与AQ之间的关系,请画出图形并直接写出结论.
24.已知,△ABC中,点D,E分别在边AB,BC上,BD=BE,连接CD.
(1)如图1,若∠CAD=∠CED=2∠ADC,求证:AD=DE;
(2)如图2,点F在AD上,连接EF,若∠CAD=∠AFE,∠CEF=2∠ADC,求证:AD=EF.
参考答案
一.选择题
1.解:∵AD是△ABC的中线,
∴BD=CD,又∠CDE=∠BDF,DE=DF,
∴△BDF≌△CDE,故④正确;
由△BDF≌△CDE,可知CE=BF,故①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD等底等高,
∴△ABD和△ACD面积相等,故②正确;
由△BDF≌△CDE,可知∠FBD=∠ECD
∴BF∥CE,故③正确.
故选:D.
2.解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;
②∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,本选项正确;
③∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,本选项正确;
④∵∠BAC=∠DAE=90°,
∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故此选项正确,
故选:D.
3.解:∵△ABC的高AD、BE,
∴∠AEB=∠BDA,
在Rt△AEB和Rt△BDA中,
,
∴Rt△AEB≌Rt△BDA(HL),
∴AE=BD,∠DAB=∠EBA,
∴AH=BH,
∵AD=BE,
∴AD﹣AH=BE﹣BH,
∴EH=DH,∴①②③④都正确;
故选:D.
4.解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=40°,
∴∠C=∠EDC=70°,
∴∠BDE=∠C=70°.
故选:D.
5.证明:∵AE∥DF,
∴∠EAB=∠FDC,
∵BE∥CF,
∴∠EBC=∠BCF,
∴∠ABE=∠FCD,
∵AC=BD,
∴AB=CD,
在△AEB和△DFC中,
,
△AEB≌△DFC(ASA),
∴BE=CF,
在△EBD和△FCA中,
,
∴△EBD≌△FCA(SAS),
∴ED=AF.
故A,B,C选项正确,
AE=CE说法不正确,
故选:D.
6.解:∵AB=AC,E、F分别是AB、AC的中点,
∴AE=BE=AB,AF=CF=AC,
∴AE=AF,BE=CF,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠B=∠C,
在△EBD和△FCD中,
,
∴△EBD≌△FCD(AAS).
∴DE=DF,
在△AED和△AFD中,
,
∴△AED≌△AFD(SSS),
∴∠EAD=∠FAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
∴此图中全等三角形有4对.
故选:C.
7.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE,①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD面积相等,②正确;
∵△BDF≌△CDE,
∴∠F=∠CDF,
∴BF∥CE,③正确;
∵△BDF≌△CDE,
∴CE=BF,④正确,
故选:D.
8.解:在△ABC和△DEB中,
∵,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
在△BCF中,由三角形的外角性质得,∠ACB+∠DBE=∠AFB,
∴∠ACB=∠AFB.
故选:B.
9.解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确
∴∠EAB=∠FAC=40°,故①正确,
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确,
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故③错误,
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故④错误.
故选:C.
10.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,故①③正确;
∠EAF=∠BAC,
∴∠EAB=∠FAC,故④正确;
∵AF≠BF,
∴∠BAF≠∠B,故②错误;
综上所述,结论正确的是①③④共3个.
故选:C.
11.解:①∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等;
故①正确;
②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确;
③∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,,
∴△BDF≌△CDE(SAS).
故③正确;
④∵△BDF≌△CDE,
∴∠CED=∠BFD,
∴BF∥CE;
故④正确;
⑤∵△BDF≌△CDE,
∴CE=BF,
∴只有当AE=BF时,CE=AE.
故⑤不一定正确.
综上所述,正确的结论是:①③④,共有3个.
故选:C.
12.解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,,
∴△ABD≌△EBC(SAS),①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,AD=EC,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,②正确;
③由②得:∠BDC=∠BEA,
又∵∠ADE=∠BDC,
∴∠ADE=∠BEA,
∴AD=AE,
∴AD=AE=EC,③正确;
④∵AD=AE=EC,AE+CE>AD+CD,
∴AD>CD,
∴AC≠2CD,故④错误,
故选:C.
13.证明:∵FC∥AB
∴∠FCE=∠DAE,
在△CFE和△ADE中
,
∴△CFE≌△ADE(ASA),
∴AD=CF=5,
∵AB=3,
∴BD=5﹣3=2,
故选:D.
二.填空题
14.解:添加∠C=∠B,理由如下:
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
故答案为:∠C=∠B(答案不唯一).
15.解:所添条件为BC=ED;
∵AB=AE,AC=AD,BC=ED
∴△ABC≌△AED(SSS).
故填BC=ED.
16.解:添加条件AC=DF可使得△ABC≌△DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF,
故答案为:AC=DF.
17.解:∵AC=DB,AO=DO,
∴BO=CO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=DC,
∵CD=200m,
∴AB=200m,
即A,B两点间的距离是200m,
故答案为:200.
18.解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
19.解:带①②去,符合ASA判定,选项符合题意;
带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故答案为:①.
20.解:在△ABC和△MBC中,
,
∴△MBC≌△ABC(ASA),
故答案为:ASA.
三.解答题
21.证明:(1)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠CBA=∠FED;
(2)∵∠CBA=∠FED,
∴ME=MB,且∠AEM=∠DBM,
∵AB=DE,
∴AB﹣EB=DE﹣EB,
即AE=DB,
在△AEM和△DBM中,
,
∴△AEM≌△DBM(SAS),
∴AM=DM.
22.(1)证明:∵DE=AB+DC,AB=AD,
∴DE=AD+DC=AC,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(SSS).
(2)解:∵△ABC≌△DAE,
∴∠EAD=∠B,
∴∠B+∠BAC=∠EAD+∠BAC=∠EAB=125°,
∴∠DCB=180°﹣(∠B+∠BAC)=180°﹣125°=55°.
23.解:(1)设CE、BD交于F,
∵BD、CE是△ABC高,
∴∠BEF=∠CDF=90°,
∵∠BFE=∠CFD,
∴∠1=180°﹣∠BEF﹣∠BFE=90°﹣∠BFE,∠2=180°﹣∠CDF﹣∠CFD=90°﹣∠CDF,
∴∠1=∠2;
故答案为:=;
(2)结论:AP=AQ,AP⊥AQ,
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(3)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
24.证明:(1)∵BD=BE,
∴∠BDE=∠BED,
∴∠ADE=∠CED,
∵∠CAD=∠CED=2∠ADC,
∴∠ADC=∠EDC=∠CED=∠ADE,
在△ADC和△EDC中,
,
∴△ADC≌△EDC(AAS),
∴AD=DE;
(2)在EC上截取EG=DF,连接DG,如图2所示:
∵BD=BE,
∴BD+DF=BE+EG,
即BF=BG,
在△BDG和△BEF中,
,
∴△BDG≌△BEF(SAS),
∴DG=EF,∠BGD=∠BFE,∠BDG=∠BEF,
∴∠ADG=∠CEF,∠CGD=∠AFE,
∵∠CAD=∠AFE,∠CEF=2∠ADC,
∴∠ADC=∠CEF=∠ADG=∠GDC,∠CAD=∠CGD,
在△ADC和△GDC中,
,
∴△ADC≌△GDC(AAS),
∴AD=GD,
∴AD=EF.
一.选择题
1.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,H是△ABC的高AD、BE的交点,且AD=BE,则下列结论中正确的有①AE=BD,②AH=BH,③EH=DH,④∠HAB=∠HBA( )
A.1个 B.2个 C.3个 D.4个
4.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
5.如图,已知AE∥DF,BE∥CF,AC=BD,则下列说法错误的是( )
A.△AEB≌△DFC B.△EBD≌△FCA C.ED=AF D.EA=EC
6.如图,AB=AC,E、F分别是AB、AC的中点,BF、CE交于点D,连接AD.则此图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
7.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠AFB C.∠BED D.∠ABF
9.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°,正确的个数为( )个.
A.1 B.2 C.3 D.4
10.如图,已知△ABC≌△AEF,其中AB=AE,∠B=∠E.在下列结论①AC=AF,②∠BAF=∠B,③EF=BC,④∠BAE=∠CAF中,正确的个数有( )
A.1个 B.2个 C.3个 D.4个
11.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:
①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.
A.1 B.2 C.3 D.4
13.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
二.填空题
14.如图,已知AC=AB,要使△ABE≌△ACD,则需添加一个条件 .
15.如图,AB=AE,AC=AD,只要 (添加一个条件即可),就可得△ABC≌△AED.
16.如图,BC=EF,∠1=∠F.请你添加一个适当的条件 ,使得△ABC≌△DEF(只需填一个答案即可).
17.如图,AC=DB,AO=DO,CD=200m,则A,B两点间的距离为 m.
18.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第 块.
19.小良打碎了一块三角形玻璃如图所示,现在他要去玻璃店配一块完全一样的玻璃,如果他带了两块玻璃,其中有一块是②,另一块是 .
20.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=65°,∠ACB=35°,然后在M处立了标杆,使∠MBC=65°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里得到△MBC≌△ABC的依据是 .
三.解答题
21.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,点 A、E、B、D在同一直线上,BC、EF交于点M,AC=DF,AB=DE.
求证:(1)∠CBA=∠FED;
(2)AM=DM.
22.如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE;
(2)若∠BAE=125°,求∠DCB的度数.
23.如图所示,BD、CE是△ABC高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)判断:∠1 ∠2(用“>”、“<”、“=”填空);
(2)探究:PA与AQ之间的关系;
(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究PA与AQ之间的关系,请画出图形并直接写出结论.
24.已知,△ABC中,点D,E分别在边AB,BC上,BD=BE,连接CD.
(1)如图1,若∠CAD=∠CED=2∠ADC,求证:AD=DE;
(2)如图2,点F在AD上,连接EF,若∠CAD=∠AFE,∠CEF=2∠ADC,求证:AD=EF.
参考答案
一.选择题
1.解:∵AD是△ABC的中线,
∴BD=CD,又∠CDE=∠BDF,DE=DF,
∴△BDF≌△CDE,故④正确;
由△BDF≌△CDE,可知CE=BF,故①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD等底等高,
∴△ABD和△ACD面积相等,故②正确;
由△BDF≌△CDE,可知∠FBD=∠ECD
∴BF∥CE,故③正确.
故选:D.
2.解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;
②∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,本选项正确;
③∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,本选项正确;
④∵∠BAC=∠DAE=90°,
∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故此选项正确,
故选:D.
3.解:∵△ABC的高AD、BE,
∴∠AEB=∠BDA,
在Rt△AEB和Rt△BDA中,
,
∴Rt△AEB≌Rt△BDA(HL),
∴AE=BD,∠DAB=∠EBA,
∴AH=BH,
∵AD=BE,
∴AD﹣AH=BE﹣BH,
∴EH=DH,∴①②③④都正确;
故选:D.
4.解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=40°,
∴∠C=∠EDC=70°,
∴∠BDE=∠C=70°.
故选:D.
5.证明:∵AE∥DF,
∴∠EAB=∠FDC,
∵BE∥CF,
∴∠EBC=∠BCF,
∴∠ABE=∠FCD,
∵AC=BD,
∴AB=CD,
在△AEB和△DFC中,
,
△AEB≌△DFC(ASA),
∴BE=CF,
在△EBD和△FCA中,
,
∴△EBD≌△FCA(SAS),
∴ED=AF.
故A,B,C选项正确,
AE=CE说法不正确,
故选:D.
6.解:∵AB=AC,E、F分别是AB、AC的中点,
∴AE=BE=AB,AF=CF=AC,
∴AE=AF,BE=CF,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠B=∠C,
在△EBD和△FCD中,
,
∴△EBD≌△FCD(AAS).
∴DE=DF,
在△AED和△AFD中,
,
∴△AED≌△AFD(SSS),
∴∠EAD=∠FAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
∴此图中全等三角形有4对.
故选:C.
7.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE,①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD面积相等,②正确;
∵△BDF≌△CDE,
∴∠F=∠CDF,
∴BF∥CE,③正确;
∵△BDF≌△CDE,
∴CE=BF,④正确,
故选:D.
8.解:在△ABC和△DEB中,
∵,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
在△BCF中,由三角形的外角性质得,∠ACB+∠DBE=∠AFB,
∴∠ACB=∠AFB.
故选:B.
9.解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确
∴∠EAB=∠FAC=40°,故①正确,
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确,
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故③错误,
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故④错误.
故选:C.
10.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,故①③正确;
∠EAF=∠BAC,
∴∠EAB=∠FAC,故④正确;
∵AF≠BF,
∴∠BAF≠∠B,故②错误;
综上所述,结论正确的是①③④共3个.
故选:C.
11.解:①∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等;
故①正确;
②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确;
③∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,,
∴△BDF≌△CDE(SAS).
故③正确;
④∵△BDF≌△CDE,
∴∠CED=∠BFD,
∴BF∥CE;
故④正确;
⑤∵△BDF≌△CDE,
∴CE=BF,
∴只有当AE=BF时,CE=AE.
故⑤不一定正确.
综上所述,正确的结论是:①③④,共有3个.
故选:C.
12.解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,,
∴△ABD≌△EBC(SAS),①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,AD=EC,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,②正确;
③由②得:∠BDC=∠BEA,
又∵∠ADE=∠BDC,
∴∠ADE=∠BEA,
∴AD=AE,
∴AD=AE=EC,③正确;
④∵AD=AE=EC,AE+CE>AD+CD,
∴AD>CD,
∴AC≠2CD,故④错误,
故选:C.
13.证明:∵FC∥AB
∴∠FCE=∠DAE,
在△CFE和△ADE中
,
∴△CFE≌△ADE(ASA),
∴AD=CF=5,
∵AB=3,
∴BD=5﹣3=2,
故选:D.
二.填空题
14.解:添加∠C=∠B,理由如下:
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
故答案为:∠C=∠B(答案不唯一).
15.解:所添条件为BC=ED;
∵AB=AE,AC=AD,BC=ED
∴△ABC≌△AED(SSS).
故填BC=ED.
16.解:添加条件AC=DF可使得△ABC≌△DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF,
故答案为:AC=DF.
17.解:∵AC=DB,AO=DO,
∴BO=CO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=DC,
∵CD=200m,
∴AB=200m,
即A,B两点间的距离是200m,
故答案为:200.
18.解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
19.解:带①②去,符合ASA判定,选项符合题意;
带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故答案为:①.
20.解:在△ABC和△MBC中,
,
∴△MBC≌△ABC(ASA),
故答案为:ASA.
三.解答题
21.证明:(1)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠CBA=∠FED;
(2)∵∠CBA=∠FED,
∴ME=MB,且∠AEM=∠DBM,
∵AB=DE,
∴AB﹣EB=DE﹣EB,
即AE=DB,
在△AEM和△DBM中,
,
∴△AEM≌△DBM(SAS),
∴AM=DM.
22.(1)证明:∵DE=AB+DC,AB=AD,
∴DE=AD+DC=AC,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(SSS).
(2)解:∵△ABC≌△DAE,
∴∠EAD=∠B,
∴∠B+∠BAC=∠EAD+∠BAC=∠EAB=125°,
∴∠DCB=180°﹣(∠B+∠BAC)=180°﹣125°=55°.
23.解:(1)设CE、BD交于F,
∵BD、CE是△ABC高,
∴∠BEF=∠CDF=90°,
∵∠BFE=∠CFD,
∴∠1=180°﹣∠BEF﹣∠BFE=90°﹣∠BFE,∠2=180°﹣∠CDF﹣∠CFD=90°﹣∠CDF,
∴∠1=∠2;
故答案为:=;
(2)结论:AP=AQ,AP⊥AQ,
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(3)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
24.证明:(1)∵BD=BE,
∴∠BDE=∠BED,
∴∠ADE=∠CED,
∵∠CAD=∠CED=2∠ADC,
∴∠ADC=∠EDC=∠CED=∠ADE,
在△ADC和△EDC中,
,
∴△ADC≌△EDC(AAS),
∴AD=DE;
(2)在EC上截取EG=DF,连接DG,如图2所示:
∵BD=BE,
∴BD+DF=BE+EG,
即BF=BG,
在△BDG和△BEF中,
,
∴△BDG≌△BEF(SAS),
∴DG=EF,∠BGD=∠BFE,∠BDG=∠BEF,
∴∠ADG=∠CEF,∠CGD=∠AFE,
∵∠CAD=∠AFE,∠CEF=2∠ADC,
∴∠ADC=∠CEF=∠ADG=∠GDC,∠CAD=∠CGD,
在△ADC和△GDC中,
,
∴△ADC≌△GDC(AAS),
∴AD=GD,
∴AD=EF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
