2022-2023学年浙教版八年级数学上册 1.5三角形全等的判定 达标测试题(Word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册 1.5三角形全等的判定 达标测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 00:00:00 | ||
图片预览




文档简介
2022-2023学年浙教版八年级数学上册《1.5三角形全等的判定》自主达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形的周长和面积分别相等
C.全等三角形是指面积相等的两个三角形
D.所有的等边三角形都是全等三角形
2.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、4或2、4或3、4去均可
5.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED的度数是( )
A.70° B.85° C.65° D.以上都不对
6.如图,AB=AD,AE平分∠BAD,则图中有( )对全等三角形.
A.2 B.3 C.4 D.5
7.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只要测量A′B′就可以,这是利用什么数学原理呢?( )
A.AAS B.SAS C.ASA D.SSS
8.如图,Rt△ABC中,CD⊥AB于D,E在AC上,过E作EF⊥AB于F,且EF=EC,连接BE交CD于G.结论:
①∠CEB=∠BEF
②CG=EF
③∠BGC=∠AEB
④∠AEF=2∠ABE
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共7小题,满分35分)
9.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是 .(填写序号)
10.如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE= cm.
11.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于 .
12.如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为 cm.
13.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C= °.
14.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论是 .
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在一条直线上.若∠3=55°,∠2=30°,则∠1的度数为 .
三.解答题(共6小题,满分45分)
16.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
17.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
18.已知:如图,在△ABC中,AB=CB,∠ABC=45°,高AD与高BE相交于点F,G为BF的中点.
求证:(1)DG=DE;
(2)∠DEG=∠DEC.
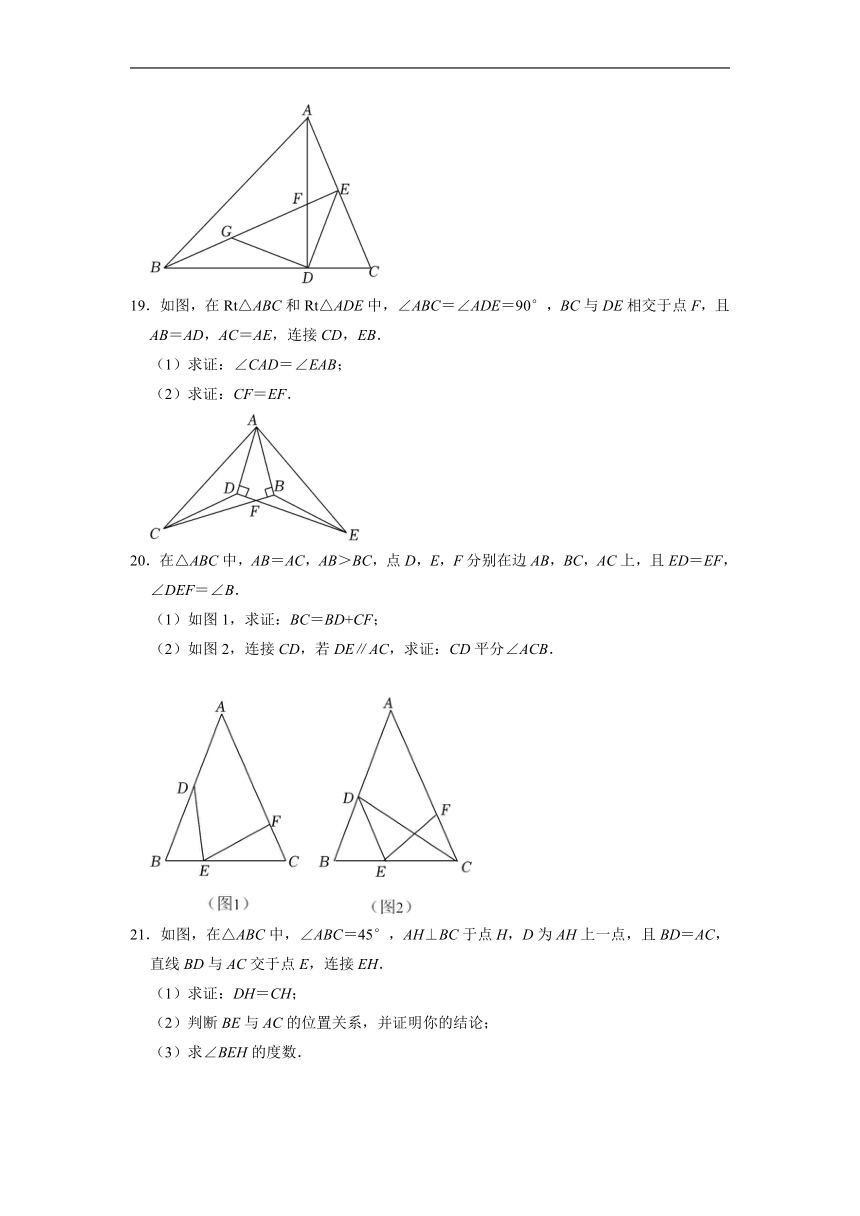
19.如图,在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,BC与DE相交于点F,且AB=AD,AC=AE,连接CD,EB.
(1)求证:∠CAD=∠EAB;
(2)求证:CF=EF.
20.在△ABC中,AB=AC,AB>BC,点D,E,F分别在边AB,BC,AC上,且ED=EF,∠DEF=∠B.
(1)如图1,求证:BC=BD+CF;
(2)如图2,连接CD,若DE∥AC,求证:CD平分∠ACB.
21.如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,D为AH上一点,且BD=AC,直线BD与AC交于点E,连接EH.
(1)求证:DH=CH;
(2)判断BE与AC的位置关系,并证明你的结论;
(3)求∠BEH的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、全等三角形的形状相同,但形状相同的两个三角形不一定是全等三角形.故该选项错误;
B、全等三角形是指能够完全重合的两个三角形,则全等三角形的周长和面积一定相等,故B正确;
C、全等三角形面积相等,但面积相等的两个三角形不一定是全等三角形.故该选项错误;
D、两个等边三角形,形状相同,但不一定能完全重合,不一定全等.故错误.
故选:B.
2.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
3.解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;
C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;
D、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;
故选:B.
4.解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选:D.
5.解:在△AOD和△BOC中
,
∴△AOD≌△BOC(SAS)
∴∠C=∠D.
∵∠C=25°,
∴∠D=25°.
∵∠O=60°,∠C=25°,
∴∠OBC=95°.
∴∠OBC=∠BED+∠D=95°,
∴∠BED=70°.
故选:A.
6.解:∵AB=AD,AE平分∠BAD,且AE、AC为公共边,
∴△DAC≌△BAC,△DAE≌△BAE(SAS),
∴DE=BE,DC=BC,EC为公共边,
∴△DCE≌△BCE(SSS).
所以共有3对三角形全等.
故选:B.
7.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
故选:B.
8.解:∵AC⊥BC,EF⊥AB,EF=EC,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠EFB=∠ECB=90°,
∴∠FEB=∠CEB,故①正确;
或者:在Rt△BEC和Rt△BEF中,
,
∴Rt△BEC≌Rt△BEF(HL),
∴∠FEB=∠CEB,故①正确;
∵∠FEB=∠CEB=90°﹣∠EBF,∠BGD=∠CGE=90°﹣∠GBD,
∴∠CEB=∠CGE,
∴CE=CG,
∵EF=EC,
∴CG=EF,故②正确;
∵∠BGC=180°﹣∠CGE,∠AEB=180°﹣∠CEG,∠CEG=∠CGE,
∴∠BGC=∠AEB,故③正确;
∵∠AEF=90°﹣∠A,∠ABC=90°﹣∠A,
∴∠AEF=∠ABC,
∵∠ABC=2∠ABE,
∴∠AEF=2∠ABE,故④正确.
综上所述:正确的结论有①②③④,共4个,
故选:D.
二.填空题(共7小题,满分35分)
9.解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,
加①AB=AE,就可以用SAS判定△ABC≌△AED;
加③∠C=∠D,就可以用ASA判定△ABC≌△AED;
加④∠B=∠E,就可以用AAS判定△ABC≌△AED;
加②BC=ED只是具备SSA,不能判定三角形全等.
其中能使△ABC≌△AED的条件有:①③④;
故答案为①③④.
10.解:∵BF⊥AC,
∴∠C+∠FBC=90°,
∵AD⊥BC,
∴∠C+∠DAC=90°,
∴∠DAC=∠FBC,
在△BDE和△ADC中
,
∴△BDE≌△ADC(ASA),
∴CD=DE=2cm,
∵BC=6cm,DC=2cm,
∴BD=AD=4cm,
∴AE=4﹣2=2(cm).
故答案为:2.
11.解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,
∵M是BC中点,∴BM=CM,∠BMN=∠CMF,
∴△BMN≌△CMF,∴BN=CF,∠N=∠MFC,
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,
∴FC=(AB+AC)=5.5.
故答案为5.5.
12.解:∵AB⊥AC,CD⊥AC,DE⊥BC,
∴∠ACD=∠BAC=∠1=90°,
∴∠B+∠BCA=90°,∠DEC+∠BCA=90°,
∴∠DEC=∠B,
在△ACB与△CDE中,
∴△ACB≌△CDE(ASA),
∴DE=BC=5cm.
故答案为:5.
13.解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠B=∠C,
∵∠B=20°,
∴∠C=20°,
故答案为20.
14.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF,
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故④正确;
故答案为:①②③④
15.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠2,
∵∠3=∠ABD+∠1,
∴∠1=∠3﹣∠2=55°﹣30°=25°.
故答案为:25°.
三.解答题(共6小题,满分45分)
16.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠ABE=∠DBE+∠ABE,
∴∠ABD=∠CBE.
在△ADB和△CEB中,
,
∴△ADB≌△CEB(SAS),
∴AD=CE;
(2)解:∵BA=BC,∠ABC=30°,
∴∠BAC=∠BCA=(180°﹣30°)=75°,
∵∠AFC=45°,
∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,
∵△ADB≌△CEB,
∴∠BAD=∠BCE=15°,
∴∠EAC=∠BAD+∠BAC=15°+75°=90°.
17.(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAG,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
18.证明:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
,
∴△BDF≌△ACD(AAS),
∴BF=AC,
∵G为BF的中点.
∴DG=BF,
∵AB=CB,BE⊥AC,
∴E为AC的中点.
∴DE=AC,
∴DG=DE;
(2)由(1)知:∠DBG=∠DAE,BG=BF,AE=AC,BF=AC,
∴BG=AE,
在△BDG和△ADE中,
,
∴△BDG≌△ADE(SAS),
∴∠BDG=∠ADE,
∴∠DGB=∠DBG+∠BDG,
∵∠DEC=∠DAE+∠ADE,
∴∠DGB=∠DEC,
∵DG=DE,
∴∠DGE=∠DEG,
∴∠DEG=∠DEC.
19.证明:(1)在Rt△ABC和Rt△ADE中,
,
∴Rt△ABC≌Rt△ADE(HL),
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAB=∠DAE﹣∠DAB,
∴∠CAD=∠EAB.
(2)在△ACD与△AEB中
,
∴△ADC≌△ABE(SAS),
∴CD=BE,∠ACD=∠AEB.
∵Rt△ABC≌Rt△ADE,
∴∠ACB=∠AED.∠ACB﹣∠ACD=∠AED﹣∠AEB,
∴∠DCF=∠BEF.∠DFC=∠BFE,
∴△DFC≌△BFE(AAS),
∴CF=EF.
20.证明:(1)如图1中,∵AB=AC,
∴∠B=∠C,
∵∠DEC=∠DEF+∠FEC=∠EDB+∠B,
∵∠DEF=∠B,
∴∠BDE=∠FEC,
∵ED=EF,
∴△BDE≌△CEF(AAS),
∴BD=EC,BE=CF,
∴BC=BE+EC=BD+CF;
(2)如图2中,∵AB=AC,
∴∠B=∠ACB,
∵DE∥AC,
∴∠DEB=∠ACB,∠EDC=∠ACD,
∴∠B=∠DEB,
∴DB=DE,
由(1)可知,BD=EC,
∴DE=EC,
∴∠EDC=∠BCD,
∴∠BCD=∠ACD,
∴CD平分∠ACB.
21.(1)证明:∵AH⊥BC,
∴∠AHB=∠AHC=90°
∵∠ABC=45°,
∴∠BAH=45°=∠ABC,
∴AH=BH,
在Rt△BHD和Rt△AHC中,
,
∴Rt△BHD≌Rt△AHC(HL),
∴DH=CH;
(2)解:BE⊥AC.
由(1)可知△BHD≌△AHC,
∴∠DBH=∠CAH.
∵∠CAH+∠C=90°,
∴∠DBH+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC;
(3)解:过点H作HF⊥HE,交BE于F点,
∴∠FHE=90°,
即∠AHE+∠DHF=90°.
又∵∠BHF+∠DHF=90°,
∴∠AHE=∠BHF,
在△AHE和△BHF中,
,
∴△AHE≌△BHF(ASA),
∴EH=FH.
∵∠FHE=90°,
∴△FHE是等腰直角三角形,
∴∠BEH=45°.
一.选择题(共8小题,满分40分)
1.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形的周长和面积分别相等
C.全等三角形是指面积相等的两个三角形
D.所有的等边三角形都是全等三角形
2.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、4或2、4或3、4去均可
5.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED的度数是( )
A.70° B.85° C.65° D.以上都不对
6.如图,AB=AD,AE平分∠BAD,则图中有( )对全等三角形.
A.2 B.3 C.4 D.5
7.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只要测量A′B′就可以,这是利用什么数学原理呢?( )
A.AAS B.SAS C.ASA D.SSS
8.如图,Rt△ABC中,CD⊥AB于D,E在AC上,过E作EF⊥AB于F,且EF=EC,连接BE交CD于G.结论:
①∠CEB=∠BEF
②CG=EF
③∠BGC=∠AEB
④∠AEF=2∠ABE
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共7小题,满分35分)
9.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是 .(填写序号)
10.如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE= cm.
11.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于 .
12.如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为 cm.
13.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C= °.
14.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论是 .
15.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在一条直线上.若∠3=55°,∠2=30°,则∠1的度数为 .
三.解答题(共6小题,满分45分)
16.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
17.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
18.已知:如图,在△ABC中,AB=CB,∠ABC=45°,高AD与高BE相交于点F,G为BF的中点.
求证:(1)DG=DE;
(2)∠DEG=∠DEC.
19.如图,在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,BC与DE相交于点F,且AB=AD,AC=AE,连接CD,EB.
(1)求证:∠CAD=∠EAB;
(2)求证:CF=EF.
20.在△ABC中,AB=AC,AB>BC,点D,E,F分别在边AB,BC,AC上,且ED=EF,∠DEF=∠B.
(1)如图1,求证:BC=BD+CF;
(2)如图2,连接CD,若DE∥AC,求证:CD平分∠ACB.
21.如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,D为AH上一点,且BD=AC,直线BD与AC交于点E,连接EH.
(1)求证:DH=CH;
(2)判断BE与AC的位置关系,并证明你的结论;
(3)求∠BEH的度数.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、全等三角形的形状相同,但形状相同的两个三角形不一定是全等三角形.故该选项错误;
B、全等三角形是指能够完全重合的两个三角形,则全等三角形的周长和面积一定相等,故B正确;
C、全等三角形面积相等,但面积相等的两个三角形不一定是全等三角形.故该选项错误;
D、两个等边三角形,形状相同,但不一定能完全重合,不一定全等.故错误.
故选:B.
2.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
3.解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;
C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;
D、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;
故选:B.
4.解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选:D.
5.解:在△AOD和△BOC中
,
∴△AOD≌△BOC(SAS)
∴∠C=∠D.
∵∠C=25°,
∴∠D=25°.
∵∠O=60°,∠C=25°,
∴∠OBC=95°.
∴∠OBC=∠BED+∠D=95°,
∴∠BED=70°.
故选:A.
6.解:∵AB=AD,AE平分∠BAD,且AE、AC为公共边,
∴△DAC≌△BAC,△DAE≌△BAE(SAS),
∴DE=BE,DC=BC,EC为公共边,
∴△DCE≌△BCE(SSS).
所以共有3对三角形全等.
故选:B.
7.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
故选:B.
8.解:∵AC⊥BC,EF⊥AB,EF=EC,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠EFB=∠ECB=90°,
∴∠FEB=∠CEB,故①正确;
或者:在Rt△BEC和Rt△BEF中,
,
∴Rt△BEC≌Rt△BEF(HL),
∴∠FEB=∠CEB,故①正确;
∵∠FEB=∠CEB=90°﹣∠EBF,∠BGD=∠CGE=90°﹣∠GBD,
∴∠CEB=∠CGE,
∴CE=CG,
∵EF=EC,
∴CG=EF,故②正确;
∵∠BGC=180°﹣∠CGE,∠AEB=180°﹣∠CEG,∠CEG=∠CGE,
∴∠BGC=∠AEB,故③正确;
∵∠AEF=90°﹣∠A,∠ABC=90°﹣∠A,
∴∠AEF=∠ABC,
∵∠ABC=2∠ABE,
∴∠AEF=2∠ABE,故④正确.
综上所述:正确的结论有①②③④,共4个,
故选:D.
二.填空题(共7小题,满分35分)
9.解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,
加①AB=AE,就可以用SAS判定△ABC≌△AED;
加③∠C=∠D,就可以用ASA判定△ABC≌△AED;
加④∠B=∠E,就可以用AAS判定△ABC≌△AED;
加②BC=ED只是具备SSA,不能判定三角形全等.
其中能使△ABC≌△AED的条件有:①③④;
故答案为①③④.
10.解:∵BF⊥AC,
∴∠C+∠FBC=90°,
∵AD⊥BC,
∴∠C+∠DAC=90°,
∴∠DAC=∠FBC,
在△BDE和△ADC中
,
∴△BDE≌△ADC(ASA),
∴CD=DE=2cm,
∵BC=6cm,DC=2cm,
∴BD=AD=4cm,
∴AE=4﹣2=2(cm).
故答案为:2.
11.解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,
∵M是BC中点,∴BM=CM,∠BMN=∠CMF,
∴△BMN≌△CMF,∴BN=CF,∠N=∠MFC,
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,
∴FC=(AB+AC)=5.5.
故答案为5.5.
12.解:∵AB⊥AC,CD⊥AC,DE⊥BC,
∴∠ACD=∠BAC=∠1=90°,
∴∠B+∠BCA=90°,∠DEC+∠BCA=90°,
∴∠DEC=∠B,
在△ACB与△CDE中,
∴△ACB≌△CDE(ASA),
∴DE=BC=5cm.
故答案为:5.
13.解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠B=∠C,
∵∠B=20°,
∴∠C=20°,
故答案为20.
14.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF,
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故④正确;
故答案为:①②③④
15.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠2,
∵∠3=∠ABD+∠1,
∴∠1=∠3﹣∠2=55°﹣30°=25°.
故答案为:25°.
三.解答题(共6小题,满分45分)
16.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠ABE=∠DBE+∠ABE,
∴∠ABD=∠CBE.
在△ADB和△CEB中,
,
∴△ADB≌△CEB(SAS),
∴AD=CE;
(2)解:∵BA=BC,∠ABC=30°,
∴∠BAC=∠BCA=(180°﹣30°)=75°,
∵∠AFC=45°,
∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,
∵△ADB≌△CEB,
∴∠BAD=∠BCE=15°,
∴∠EAC=∠BAD+∠BAC=15°+75°=90°.
17.(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAG,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
18.证明:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
,
∴△BDF≌△ACD(AAS),
∴BF=AC,
∵G为BF的中点.
∴DG=BF,
∵AB=CB,BE⊥AC,
∴E为AC的中点.
∴DE=AC,
∴DG=DE;
(2)由(1)知:∠DBG=∠DAE,BG=BF,AE=AC,BF=AC,
∴BG=AE,
在△BDG和△ADE中,
,
∴△BDG≌△ADE(SAS),
∴∠BDG=∠ADE,
∴∠DGB=∠DBG+∠BDG,
∵∠DEC=∠DAE+∠ADE,
∴∠DGB=∠DEC,
∵DG=DE,
∴∠DGE=∠DEG,
∴∠DEG=∠DEC.
19.证明:(1)在Rt△ABC和Rt△ADE中,
,
∴Rt△ABC≌Rt△ADE(HL),
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAB=∠DAE﹣∠DAB,
∴∠CAD=∠EAB.
(2)在△ACD与△AEB中
,
∴△ADC≌△ABE(SAS),
∴CD=BE,∠ACD=∠AEB.
∵Rt△ABC≌Rt△ADE,
∴∠ACB=∠AED.∠ACB﹣∠ACD=∠AED﹣∠AEB,
∴∠DCF=∠BEF.∠DFC=∠BFE,
∴△DFC≌△BFE(AAS),
∴CF=EF.
20.证明:(1)如图1中,∵AB=AC,
∴∠B=∠C,
∵∠DEC=∠DEF+∠FEC=∠EDB+∠B,
∵∠DEF=∠B,
∴∠BDE=∠FEC,
∵ED=EF,
∴△BDE≌△CEF(AAS),
∴BD=EC,BE=CF,
∴BC=BE+EC=BD+CF;
(2)如图2中,∵AB=AC,
∴∠B=∠ACB,
∵DE∥AC,
∴∠DEB=∠ACB,∠EDC=∠ACD,
∴∠B=∠DEB,
∴DB=DE,
由(1)可知,BD=EC,
∴DE=EC,
∴∠EDC=∠BCD,
∴∠BCD=∠ACD,
∴CD平分∠ACB.
21.(1)证明:∵AH⊥BC,
∴∠AHB=∠AHC=90°
∵∠ABC=45°,
∴∠BAH=45°=∠ABC,
∴AH=BH,
在Rt△BHD和Rt△AHC中,
,
∴Rt△BHD≌Rt△AHC(HL),
∴DH=CH;
(2)解:BE⊥AC.
由(1)可知△BHD≌△AHC,
∴∠DBH=∠CAH.
∵∠CAH+∠C=90°,
∴∠DBH+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC;
(3)解:过点H作HF⊥HE,交BE于F点,
∴∠FHE=90°,
即∠AHE+∠DHF=90°.
又∵∠BHF+∠DHF=90°,
∴∠AHE=∠BHF,
在△AHE和△BHF中,
,
∴△AHE≌△BHF(ASA),
∴EH=FH.
∵∠FHE=90°,
∴△FHE是等腰直角三角形,
∴∠BEH=45°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
