浙教版八年级上册1.1认识三角形课件(共27张PPT)
文档属性
| 名称 | 浙教版八年级上册1.1认识三角形课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 11:20:38 | ||
图片预览




文档简介
(共27张PPT)
1.1认识三角形(1)
浙教版数学八年级上册第一章第一节
目 录
教材
分析
教学
目标
教学
过程
教法
学法
评价分析
学情分析
本节课选自浙教版《义务教育教科书·数学》八年级上册《1.1认识三角形》第一课时。具体介绍了三角形的定义及其有关概念、三角形的内角和定理以及三角形三边之间的关系。学生在七年级上学期学习了线段、射线、直线和角等几何图形,七年级下学期学行线的相关知识,积累了一定的几何图形的研究经验。同时三角形又是最简单的多边形,也是认识学习其他几何图形的基础。因此,本节课作为章节起始课,除了显性知识外,还承载着单元知识,几何图形的学习方法、研究方向的引领作用.
一.教材分析
小学已经学习了有关三角形的一些初步知识
积累了一定的几何图形的研究经验
经验
逻辑推理能力,概括能力
不足
学生已有经验及不足
二.学情分析
教学目标
01
进一步认识三角形的概念,会用符号、字母表示三角形.
02
经历观察、猜想、实验、证明”三角形任何两边的
和大于第三边“的活动过程,发展概括能力、逻辑推理能力
04
03
三.教学目标
了解三角形按角分类.
理解”三角形任何两边的和大于第三边“的性质
判断三条线段能否组成三角形,过程较为复杂,是本节教学的难点
“三角形任何两边的和大于第三边”的性质
重 点
难 点
重难点
1
问题驱动
3
自主探索
4
合作交流
2
启发教学
教法
学法
四.教法学法
1
2
3
4
5
学以致用,巩固新知
小结梳理,总结提升
布置作业,巩固提高
复习回顾,引入新知
自主探索,合作交流
五.教学过程
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
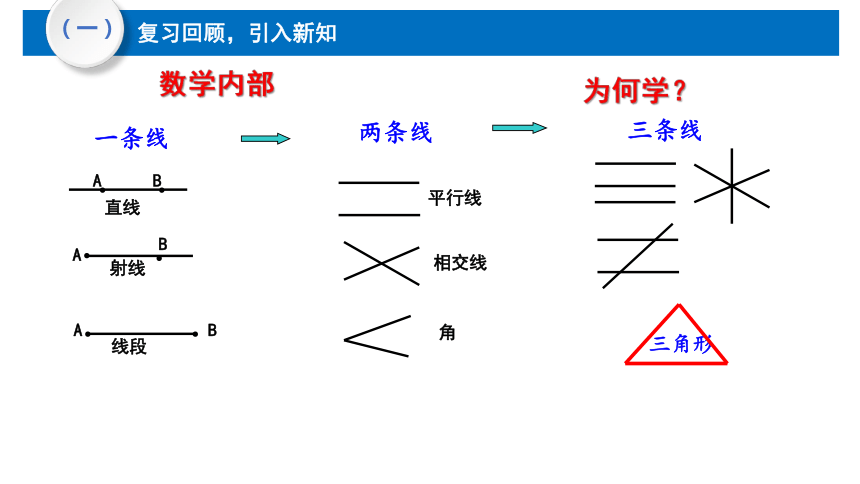
数学内部
复习回顾,引入新知
为何学?
(一)
【设计意图】通过从数学内部和生活现实两个方面明确研究对象(三角形)形成的背景和过程,让学生体会三角形学习的必要性和重要性,激发学生主动研究的欲望。
生活现实
回顾“线段和角”的研究过程,我们研究了哪些内容?是按怎样的路径展开研究的?
唤醒已有的知识与经验
定义——表示——分类——性质——特例
【设计意图】引导学生回顾“线段和角”的研究路径,为三角形的研究埋下伏笔,让学生既见树木,又见森林,形成整体知识框架。
1.动手画一个三角形;
2.对于三角形,你有哪些认识?
自主探索,合作交流
探究活动一
【设计意图】学生在小学已经初步学习了三角形,依据这个最近发展区,让学生自己动手画一画、并回顾对三角形已有的认识,学生可畅所欲言,唤醒学生已有的知识和经验,尊重学生已有的认知发展水平,充分体现了新课标“以生为本”的理念。
3.你能给三角形下个定义吗?
不在同一条直线上 首尾顺次相接
(二)
如何表示三角形?
∠AOB
类比
A
B
C
记作 “ΔABC”
读作“三角形ABC”
【设计意图】学生已经有了表示角的经验,此环节学生先尝试回答,在学生回答的基础上教师完善,感受数学符号表达的简洁性、明确性、抽象性、逻辑性等特点,同时渗透类比的数学思想方法。
自主探索,合作交流
(二)
A
B
C
BC 、 AC 、AB
内角:
∠A、∠B、 ∠C
点A、 点 B、 点 C
a
c
b
或a、 b、 c
三边:
顶点:
三角形的构成元素
【设计意图】让学生认识三角形的构成元素,引领学生关注三种语言图形语言、文字语言、符号语言的表述及相互转化。
自主探索,合作交流
(二)
锐角三角形
直角三角形
钝角三角形
(三个内角都是锐角)
(有一个内角是直角)
(有一个内角是钝角)
三角形按内角的大小分类
三角形的分类
小组讨论:还有其他的分类方法吗?
【设计意图】按角分类学生一开始就很容易想到,可以通过提问“还有其他分类方法吗”引发学生思考。力求尽可能得发挥学生主观能动性,调动学生思维。同时,在生生交流过程中,教师给予适当指导和引领,并指导学生体会分类的思想方法。
自主探索,合作交流
(二)
三角形的内角和等于180°,
在△ABC中,∠A+∠B+∠C=180°
三角形的性质
自主探索,合作交流
(二)
【设计意图】感受数学符号语言的简洁性,强调三种语言的相互转化。同时可向学生交代在1.3节会完成它的证明。
1.如图:
(1)图中有几个三角形?用符号表示这些三角形。
(2)以E为顶点的三角形有哪些?
你是怎么找的?
小试牛刀
(4)你还能提出些什么问题?
(3)若∠ABE=55°,∠DEC =70°,则∠A =______
【设计意图】通过练习(1)、(2)、(3)及时巩固所学知识。设置开放性问题(4),让学生自己提出问题同桌相互解答,最后全班交流展示。由学生参与提问与评价,既可以检验学生对所学知识的掌握程度,又可以培养学生的创新意识,提高学生提出问题,解决问题的能力。
自主探索,合作交流
(二)
实验几何
论证几何
【设计意图】从具体的形象思维向逻辑抽象思维的过渡,需要用逻辑推理形式去证明结论,让学生真正从“知其然”到“知其所以然”,感受“公理化思想”、培育“理性精神”。
自主探索,合作交流
(二)
例1: 长度为4cm, 6cm, 3cm三条线段能否首尾相接组成三角形?
思考:请总结判断三条线段能否组成三角形的基本步骤
练一练
(2)e=6.3cm, f=6.3cm, g=12.6cm.
(1)a=2.5cm, b=3cm, c=5cm.
判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由。
自主探索,合作交流
(二)
【设计意图】引导学生关注,每个同学的图形不同,所得结论相同。由于学生还没有学过不等式的性质,这里我将融合信息技术手段—几何画板加以验证,渗透由特殊到一般的数学思想方法。整个环节学生经历了观察、测量、猜想、验证的过程,发展了学生的合情推理能力、归纳概括能力。
自主探索,合作交流
(二)
小明要做一个三角形的铁架子,现已有两条长分别为40cm和90cm的铁条,需要再买一根铁条,把它们首尾焊接在一起.
40cm,50cm,60cm,
90cm,130cm
商店
我可以买哪几种呢?
两边之差 第三边 两边之和
【设计意图】利用三角形任何两边的和、两边的差与第三条边的之间关系,可以确定第三条边的取值范围.在这里设置想一想,目的是基于学生的最近发展区展开思维训练,以提升学生的逻辑思维.
学以致用,巩固新知
(三)
四根木棒的长度分别是12cm,8cm,5cm,6cm从中取三根,使它们首尾顺次相接组成一个三角形.一共有多少种取法?把它们都列出来。
拓展提升
学以致用,巩固新知
(三)
【设计意图】通过拓展提高,让学生体会在用列举法时,如何做到不遗漏,不重复,强调“有序”,渗透分类的数学思想方法。
1.我学到了什么数学知识?
2.我们是如何研究三角形的 通过本节课的学习,你体验了哪些数学思想?积累了哪些学习方法或经验?
3.想进一步研究的问题是...........
小结梳理,总结提升
(四)
1.必做题 :作业本
2.选做题: 设计一张由若干个三角形组成的美丽图案,并给所组的图案加一句形象的解说词.
布置作业,巩固提高
(五)
板书设计
1.1 认识三角形(1)
电子屏幕区
板演区
逻辑连贯的教学
突出了数学思想方法
及时评价,方式多样
本节课的教学设计
六.评价分析
谢谢大家!
1.1认识三角形(1)
浙教版数学八年级上册第一章第一节
目 录
教材
分析
教学
目标
教学
过程
教法
学法
评价分析
学情分析
本节课选自浙教版《义务教育教科书·数学》八年级上册《1.1认识三角形》第一课时。具体介绍了三角形的定义及其有关概念、三角形的内角和定理以及三角形三边之间的关系。学生在七年级上学期学习了线段、射线、直线和角等几何图形,七年级下学期学行线的相关知识,积累了一定的几何图形的研究经验。同时三角形又是最简单的多边形,也是认识学习其他几何图形的基础。因此,本节课作为章节起始课,除了显性知识外,还承载着单元知识,几何图形的学习方法、研究方向的引领作用.
一.教材分析
小学已经学习了有关三角形的一些初步知识
积累了一定的几何图形的研究经验
经验
逻辑推理能力,概括能力
不足
学生已有经验及不足
二.学情分析
教学目标
01
进一步认识三角形的概念,会用符号、字母表示三角形.
02
经历观察、猜想、实验、证明”三角形任何两边的
和大于第三边“的活动过程,发展概括能力、逻辑推理能力
04
03
三.教学目标
了解三角形按角分类.
理解”三角形任何两边的和大于第三边“的性质
判断三条线段能否组成三角形,过程较为复杂,是本节教学的难点
“三角形任何两边的和大于第三边”的性质
重 点
难 点
重难点
1
问题驱动
3
自主探索
4
合作交流
2
启发教学
教法
学法
四.教法学法
1
2
3
4
5
学以致用,巩固新知
小结梳理,总结提升
布置作业,巩固提高
复习回顾,引入新知
自主探索,合作交流
五.教学过程
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
数学内部
复习回顾,引入新知
为何学?
(一)
【设计意图】通过从数学内部和生活现实两个方面明确研究对象(三角形)形成的背景和过程,让学生体会三角形学习的必要性和重要性,激发学生主动研究的欲望。
生活现实
回顾“线段和角”的研究过程,我们研究了哪些内容?是按怎样的路径展开研究的?
唤醒已有的知识与经验
定义——表示——分类——性质——特例
【设计意图】引导学生回顾“线段和角”的研究路径,为三角形的研究埋下伏笔,让学生既见树木,又见森林,形成整体知识框架。
1.动手画一个三角形;
2.对于三角形,你有哪些认识?
自主探索,合作交流
探究活动一
【设计意图】学生在小学已经初步学习了三角形,依据这个最近发展区,让学生自己动手画一画、并回顾对三角形已有的认识,学生可畅所欲言,唤醒学生已有的知识和经验,尊重学生已有的认知发展水平,充分体现了新课标“以生为本”的理念。
3.你能给三角形下个定义吗?
不在同一条直线上 首尾顺次相接
(二)
如何表示三角形?
∠AOB
类比
A
B
C
记作 “ΔABC”
读作“三角形ABC”
【设计意图】学生已经有了表示角的经验,此环节学生先尝试回答,在学生回答的基础上教师完善,感受数学符号表达的简洁性、明确性、抽象性、逻辑性等特点,同时渗透类比的数学思想方法。
自主探索,合作交流
(二)
A
B
C
BC 、 AC 、AB
内角:
∠A、∠B、 ∠C
点A、 点 B、 点 C
a
c
b
或a、 b、 c
三边:
顶点:
三角形的构成元素
【设计意图】让学生认识三角形的构成元素,引领学生关注三种语言图形语言、文字语言、符号语言的表述及相互转化。
自主探索,合作交流
(二)
锐角三角形
直角三角形
钝角三角形
(三个内角都是锐角)
(有一个内角是直角)
(有一个内角是钝角)
三角形按内角的大小分类
三角形的分类
小组讨论:还有其他的分类方法吗?
【设计意图】按角分类学生一开始就很容易想到,可以通过提问“还有其他分类方法吗”引发学生思考。力求尽可能得发挥学生主观能动性,调动学生思维。同时,在生生交流过程中,教师给予适当指导和引领,并指导学生体会分类的思想方法。
自主探索,合作交流
(二)
三角形的内角和等于180°,
在△ABC中,∠A+∠B+∠C=180°
三角形的性质
自主探索,合作交流
(二)
【设计意图】感受数学符号语言的简洁性,强调三种语言的相互转化。同时可向学生交代在1.3节会完成它的证明。
1.如图:
(1)图中有几个三角形?用符号表示这些三角形。
(2)以E为顶点的三角形有哪些?
你是怎么找的?
小试牛刀
(4)你还能提出些什么问题?
(3)若∠ABE=55°,∠DEC =70°,则∠A =______
【设计意图】通过练习(1)、(2)、(3)及时巩固所学知识。设置开放性问题(4),让学生自己提出问题同桌相互解答,最后全班交流展示。由学生参与提问与评价,既可以检验学生对所学知识的掌握程度,又可以培养学生的创新意识,提高学生提出问题,解决问题的能力。
自主探索,合作交流
(二)
实验几何
论证几何
【设计意图】从具体的形象思维向逻辑抽象思维的过渡,需要用逻辑推理形式去证明结论,让学生真正从“知其然”到“知其所以然”,感受“公理化思想”、培育“理性精神”。
自主探索,合作交流
(二)
例1: 长度为4cm, 6cm, 3cm三条线段能否首尾相接组成三角形?
思考:请总结判断三条线段能否组成三角形的基本步骤
练一练
(2)e=6.3cm, f=6.3cm, g=12.6cm.
(1)a=2.5cm, b=3cm, c=5cm.
判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由。
自主探索,合作交流
(二)
【设计意图】引导学生关注,每个同学的图形不同,所得结论相同。由于学生还没有学过不等式的性质,这里我将融合信息技术手段—几何画板加以验证,渗透由特殊到一般的数学思想方法。整个环节学生经历了观察、测量、猜想、验证的过程,发展了学生的合情推理能力、归纳概括能力。
自主探索,合作交流
(二)
小明要做一个三角形的铁架子,现已有两条长分别为40cm和90cm的铁条,需要再买一根铁条,把它们首尾焊接在一起.
40cm,50cm,60cm,
90cm,130cm
商店
我可以买哪几种呢?
两边之差 第三边 两边之和
【设计意图】利用三角形任何两边的和、两边的差与第三条边的之间关系,可以确定第三条边的取值范围.在这里设置想一想,目的是基于学生的最近发展区展开思维训练,以提升学生的逻辑思维.
学以致用,巩固新知
(三)
四根木棒的长度分别是12cm,8cm,5cm,6cm从中取三根,使它们首尾顺次相接组成一个三角形.一共有多少种取法?把它们都列出来。
拓展提升
学以致用,巩固新知
(三)
【设计意图】通过拓展提高,让学生体会在用列举法时,如何做到不遗漏,不重复,强调“有序”,渗透分类的数学思想方法。
1.我学到了什么数学知识?
2.我们是如何研究三角形的 通过本节课的学习,你体验了哪些数学思想?积累了哪些学习方法或经验?
3.想进一步研究的问题是...........
小结梳理,总结提升
(四)
1.必做题 :作业本
2.选做题: 设计一张由若干个三角形组成的美丽图案,并给所组的图案加一句形象的解说词.
布置作业,巩固提高
(五)
板书设计
1.1 认识三角形(1)
电子屏幕区
板演区
逻辑连贯的教学
突出了数学思想方法
及时评价,方式多样
本节课的教学设计
六.评价分析
谢谢大家!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
