浙教版九年级上册 3.1 圆 课件(33张PPT)
文档属性
| 名称 | 浙教版九年级上册 3.1 圆 课件(33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 23:12:23 | ||
图片预览




文档简介
(共33张PPT)
生活中的圆
§3.1 圆(1)
浙教版 九年级上册
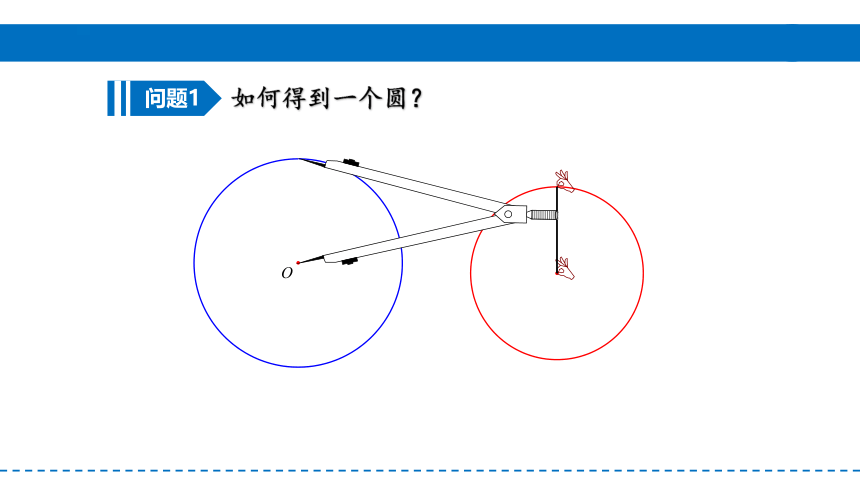
如何得到一个圆?
B
B
O
问题1
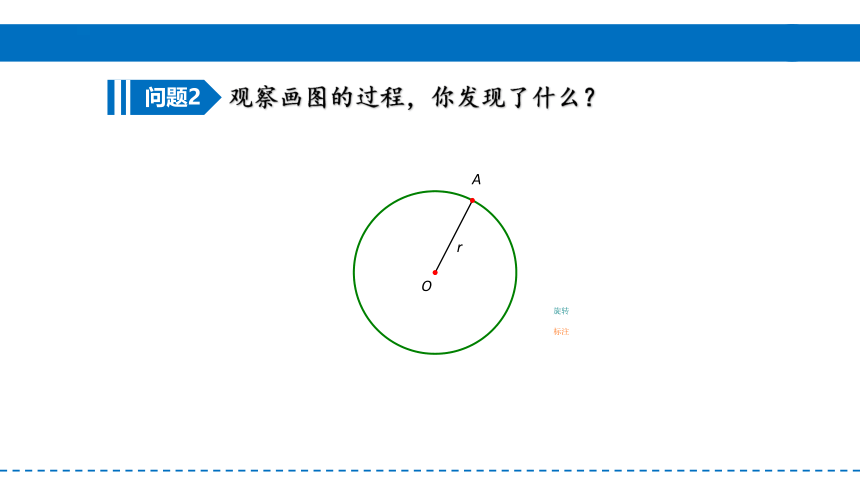
观察画图的过程,你发现了什么?
O
A
r
标注
旋转
问题2
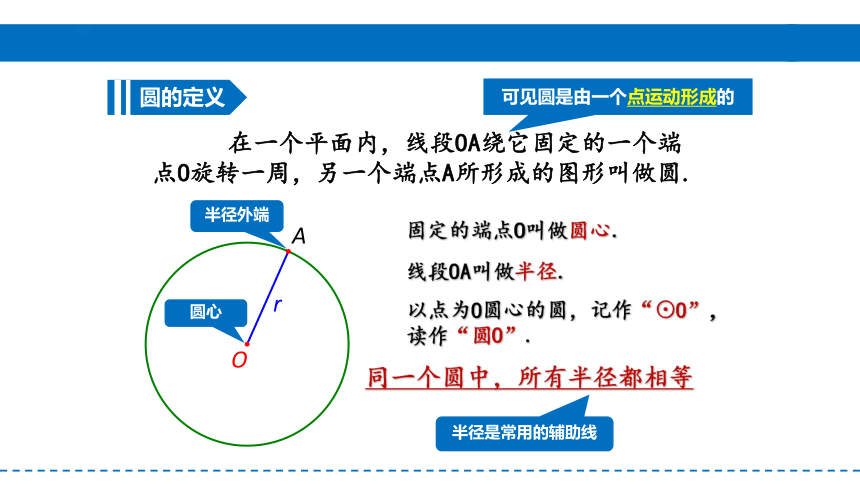
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
固定的端点O叫做圆心.
线段OA叫做半径.
以点为O圆心的圆,记作“⊙O”,
读作“圆O”.
同一个圆中,所有半径都相等
半径是常用的辅助线
可见圆是由一个点运动形成的
圆的这种记法缺陷是不能体现出圆的半径大小
圆心
O
A
r
圆的定义
半径外端
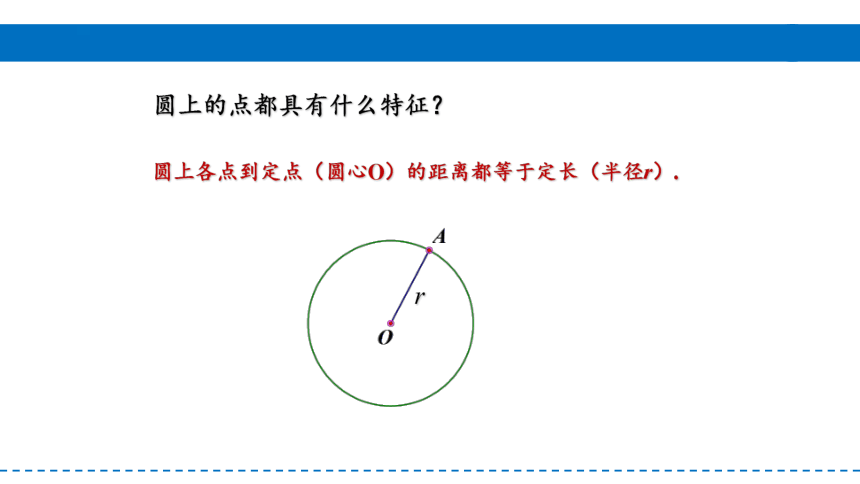
圆上各点到定点(圆心O)的距离都等于定长(半径r).
r
圆上的点都具有什么特征?
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有 “圆,一中同长也”的记载.
它的意思是圆有一个圆心,圆上各点到圆心的距离都等于半径.
圆的历史
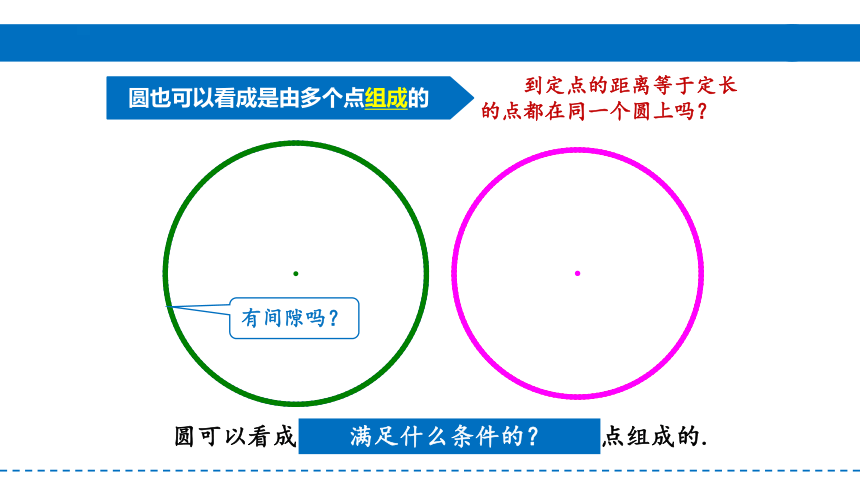
圆可以看成到定点距离等于定长的所有点组成的.
满足什么条件的?
有间隙吗?
圆也可以看成是由多个点组成的
到定点的距离等于定长
的点都在同一个圆上吗?
【静态】
【动态】
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
到定点距离等于定长的所有点的集合.
圆的两种定义
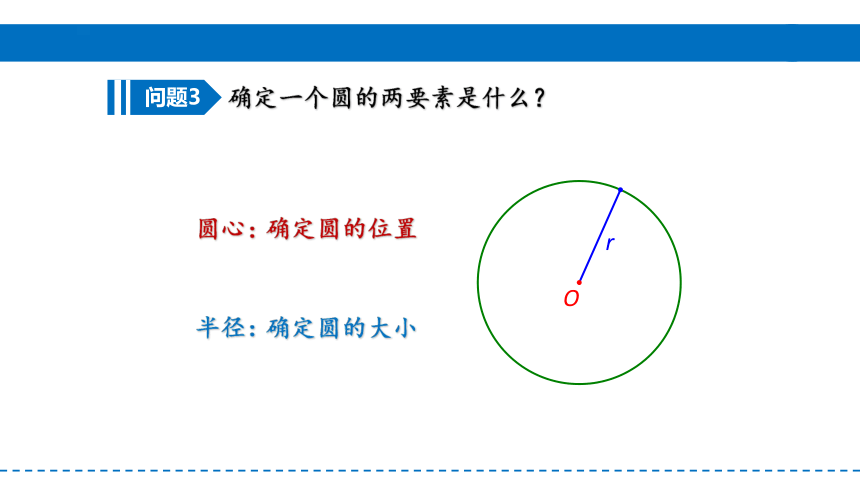
确定一个圆的两要素是什么?
圆心:
半径:
确定圆的位置
确定圆的大小
O
r
问题3
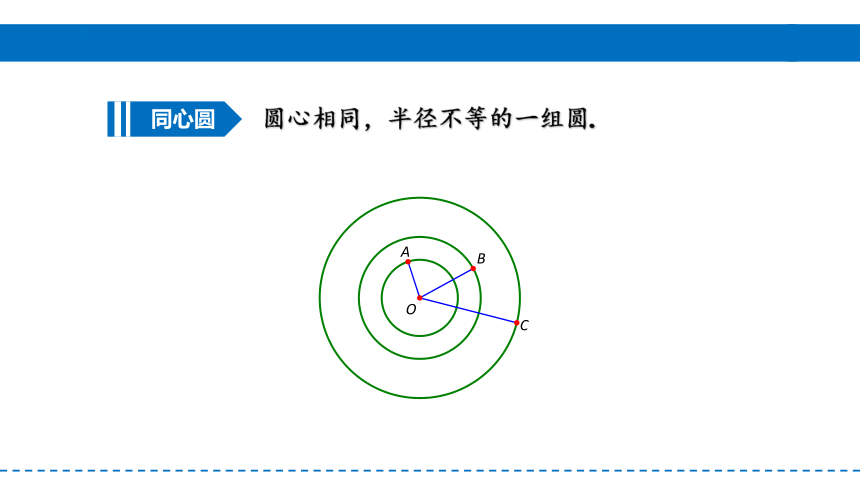
圆心相同,半径不等的一组圆.
O
A
B
C
同心圆
O1
A
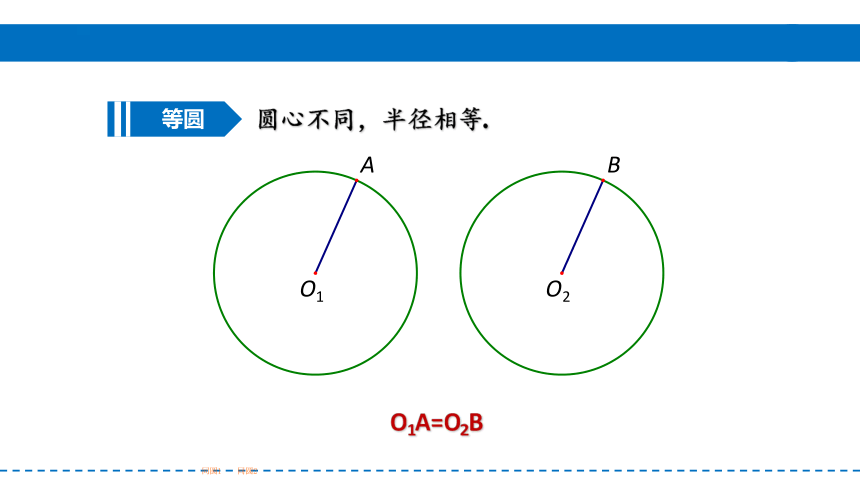
O1A=O2B
O2
B
圆心不同,半径相等.
同圆1
同圆2
等圆
圆心相同,半径也相等.
如果把这幅图看作由多个等圆叠合而成,那么这些圆……
O
A
B
C
D
E
F
G
既然它们是重合的,因此我们也时常认为同圆是“同一个圆”.
换句话说仅当作一个圆看待
同时我们还知道了在等圆中考虑问题,和在同圆中考虑问题,往往效果是一样的.
从侧面并拉开一点看看
原本是叠合的
同圆
车轮为什么要做成圆形的?
问题4
1. 弦:
连接圆上任意两点的线段.
弦AB
直径AB
【发现】直径是特殊的弦.
O
A
B
O
B
A
“直径”和“弦”有什么关系?
与圆有关的概念
特殊化
经过圆心的弦
1. 弦:
连接圆上任意两点的线段
特殊化
经过圆心的弦
【发现】直径是特殊的弦
O
B
A
弦AB
直径AB
O
A
B
与圆相关的元素
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
问题5
O
2. (圆)弧:
圆上任意两点间的部分.
A
B
B
A
B
从圆中取下一部分
这部分叫做圆弧(简称弧)
余下部分呢?
与圆有关的概念
O
A
B
A
B
O
A
B
B
A
半个圆叫做半圆
可见半圆是弧
2. (圆)弧:
圆上任意两点间的部分.
与圆有关的概念
【发现】弧可分为:
特殊化
(其中线段AB是直径)
半圆
C
劣弧,半圆,优弧.
2. (圆)弧:
圆上任意两点间的部分.
与圆有关的概念
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
AB = CD
︵
︵
A
B
C
D
A
B
C
D
同圆中
等圆中
3.等弧:
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
3.等弧:
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上,这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
3.等弧:
求证:矩形的四个顶点在以对角线交点为圆心的圆上
已知:如图,已知矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴OA=OC=0.5AC; OB=OD=0.5BD;
AC=BD
∴A、B、C、D在以O为圆心以OA为半径的圆上.
矩形的四个顶点在同一个圆上吗?
∴OA=OB=OC=OD
思考
点与圆的位置
圆上的点有什么共同特征呢?
OP1=OP2=OP3=…=OPn=r
圆心O在圆的什么位置呢?
.E
.G
.F
点E在圆内
点F在圆上
.O
.P1
.P2
.P3
Pn.
点G在圆外
现需要在A处进行一次“工程爆破”,B处有一间民房,请问需要哪些条件来判断民房是否在爆炸范围内?如何判断?
怎样判断点与圆的位置关系?
A
B
工程爆破
整理
点G在圆外
点E在圆内
点F在圆上
点与圆的位置关系
一般的,如果用r表示圆的半径,d表示同一平面内点到圆心的距离,则有
d>r
d=r
d<r
位置关系 数量关系
学以致用
1.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
2.如图,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
B
A
C
D.
2.如图,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
B
A
C
D.
变式:若BC是一条街道,为了保障街上行人的安全,问爆破影响面的半径应该控制在什么范围?
变式:要使点A,B,C中有且仅有两个点在圆内,那么⊙P的半径应满足什么条件?
A
B
C
.
P
3.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
整理
点G在
圆上
圆外
圆内
点E在
点F在
d>r
d=r
d<r
梳理
点与圆的位置关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
圆
多边形
(曲线)
(直线)
圆的相关概念
弦
弧
半圆
优弧
劣弧
(位置关系)
(数量关系)
圆的定义
……
生活中的圆
§3.1 圆(1)
浙教版 九年级上册
如何得到一个圆?
B
B
O
问题1
观察画图的过程,你发现了什么?
O
A
r
标注
旋转
问题2
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
固定的端点O叫做圆心.
线段OA叫做半径.
以点为O圆心的圆,记作“⊙O”,
读作“圆O”.
同一个圆中,所有半径都相等
半径是常用的辅助线
可见圆是由一个点运动形成的
圆的这种记法缺陷是不能体现出圆的半径大小
圆心
O
A
r
圆的定义
半径外端
圆上各点到定点(圆心O)的距离都等于定长(半径r).
r
圆上的点都具有什么特征?
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有 “圆,一中同长也”的记载.
它的意思是圆有一个圆心,圆上各点到圆心的距离都等于半径.
圆的历史
圆可以看成到定点距离等于定长的所有点组成的.
满足什么条件的?
有间隙吗?
圆也可以看成是由多个点组成的
到定点的距离等于定长
的点都在同一个圆上吗?
【静态】
【动态】
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
到定点距离等于定长的所有点的集合.
圆的两种定义
确定一个圆的两要素是什么?
圆心:
半径:
确定圆的位置
确定圆的大小
O
r
问题3
圆心相同,半径不等的一组圆.
O
A
B
C
同心圆
O1
A
O1A=O2B
O2
B
圆心不同,半径相等.
同圆1
同圆2
等圆
圆心相同,半径也相等.
如果把这幅图看作由多个等圆叠合而成,那么这些圆……
O
A
B
C
D
E
F
G
既然它们是重合的,因此我们也时常认为同圆是“同一个圆”.
换句话说仅当作一个圆看待
同时我们还知道了在等圆中考虑问题,和在同圆中考虑问题,往往效果是一样的.
从侧面并拉开一点看看
原本是叠合的
同圆
车轮为什么要做成圆形的?
问题4
1. 弦:
连接圆上任意两点的线段.
弦AB
直径AB
【发现】直径是特殊的弦.
O
A
B
O
B
A
“直径”和“弦”有什么关系?
与圆有关的概念
特殊化
经过圆心的弦
1. 弦:
连接圆上任意两点的线段
特殊化
经过圆心的弦
【发现】直径是特殊的弦
O
B
A
弦AB
直径AB
O
A
B
与圆相关的元素
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
问题5
O
2. (圆)弧:
圆上任意两点间的部分.
A
B
B
A
B
从圆中取下一部分
这部分叫做圆弧(简称弧)
余下部分呢?
与圆有关的概念
O
A
B
A
B
O
A
B
B
A
半个圆叫做半圆
可见半圆是弧
2. (圆)弧:
圆上任意两点间的部分.
与圆有关的概念
【发现】弧可分为:
特殊化
(其中线段AB是直径)
半圆
C
劣弧,半圆,优弧.
2. (圆)弧:
圆上任意两点间的部分.
与圆有关的概念
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
AB = CD
︵
︵
A
B
C
D
A
B
C
D
同圆中
等圆中
3.等弧:
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
3.等弧:
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上,这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
︵
︵
D
C
A
B
与圆有关的概念
同圆或等圆中能够完全重合的弧是等弧.
3.等弧:
求证:矩形的四个顶点在以对角线交点为圆心的圆上
已知:如图,已知矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴OA=OC=0.5AC; OB=OD=0.5BD;
AC=BD
∴A、B、C、D在以O为圆心以OA为半径的圆上.
矩形的四个顶点在同一个圆上吗?
∴OA=OB=OC=OD
思考
点与圆的位置
圆上的点有什么共同特征呢?
OP1=OP2=OP3=…=OPn=r
圆心O在圆的什么位置呢?
.E
.G
.F
点E在圆内
点F在圆上
.O
.P1
.P2
.P3
Pn.
点G在圆外
现需要在A处进行一次“工程爆破”,B处有一间民房,请问需要哪些条件来判断民房是否在爆炸范围内?如何判断?
怎样判断点与圆的位置关系?
A
B
工程爆破
整理
点G在圆外
点E在圆内
点F在圆上
点与圆的位置关系
一般的,如果用r表示圆的半径,d表示同一平面内点到圆心的距离,则有
d>r
d=r
d<r
位置关系 数量关系
学以致用
1.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
2.如图,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
B
A
C
D.
2.如图,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
B
A
C
D.
变式:若BC是一条街道,为了保障街上行人的安全,问爆破影响面的半径应该控制在什么范围?
变式:要使点A,B,C中有且仅有两个点在圆内,那么⊙P的半径应满足什么条件?
A
B
C
.
P
3.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
整理
点G在
圆上
圆外
圆内
点E在
点F在
d>r
d=r
d<r
梳理
点与圆的位置关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
圆
多边形
(曲线)
(直线)
圆的相关概念
弦
弧
半圆
优弧
劣弧
(位置关系)
(数量关系)
圆的定义
……
同课章节目录
