浙教版七年级上册 6.3 线段的长短比较 课件(17张PPT)
文档属性
| 名称 | 浙教版七年级上册 6.3 线段的长短比较 课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 778.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
6.3线段的长短比较
思考:怎样比较两个人的个子高矮?
叠合法
度量法
观察法
方法二:两个人背靠背并立于同一高度地面上
方法一:用测量仪量一下两个人的身高
方法三:直接目测(两个人高矮相差较大时)
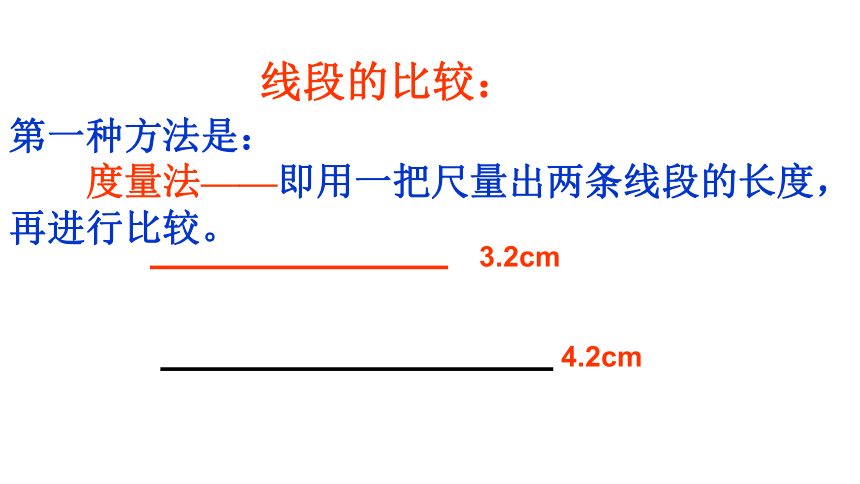
第一种方法是:
度量法——即用一把尺量出两条线段的长度,
再进行比较。
3.2cm
4.2cm
线段的比较:
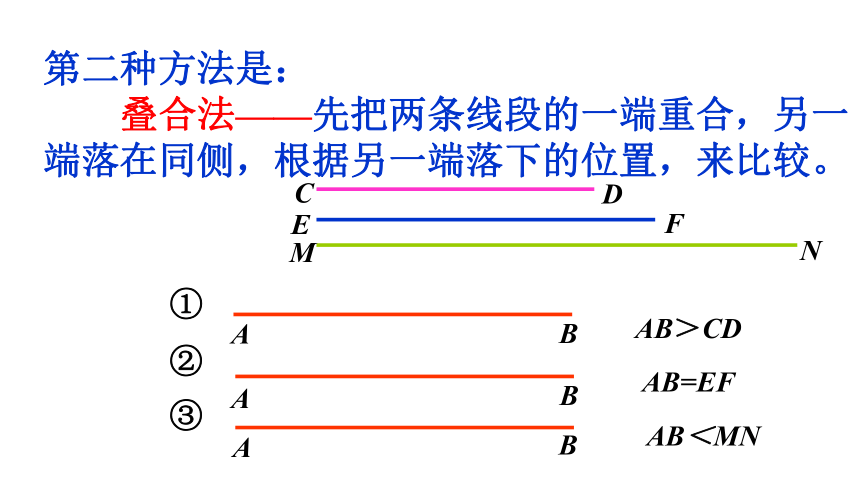
第二种方法是:
叠合法——先把两条线段的一端重合,另一
端落在同侧,根据另一端落下的位置,来比较。
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
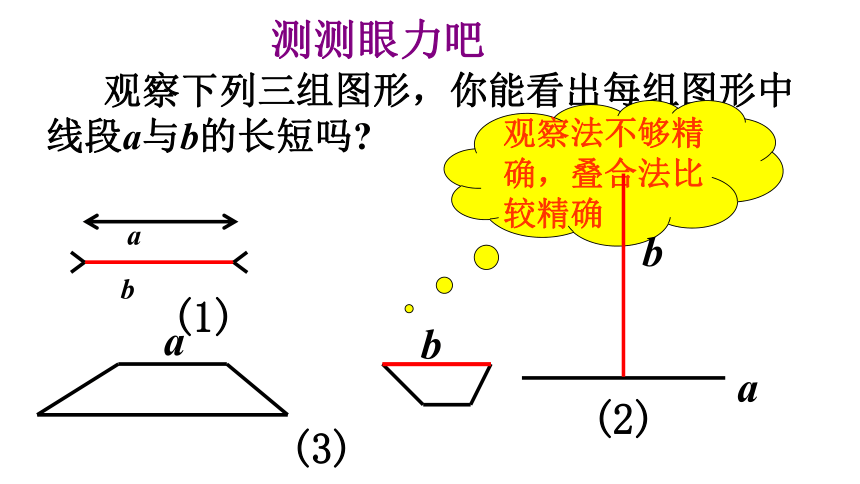
观察下列三组图形,你能看出每组图形中线段a与b的长短吗
a
b
a
b
(1)
(3)
(2)
测测眼力吧
观察法不够精确,叠合法比较精确
a
b
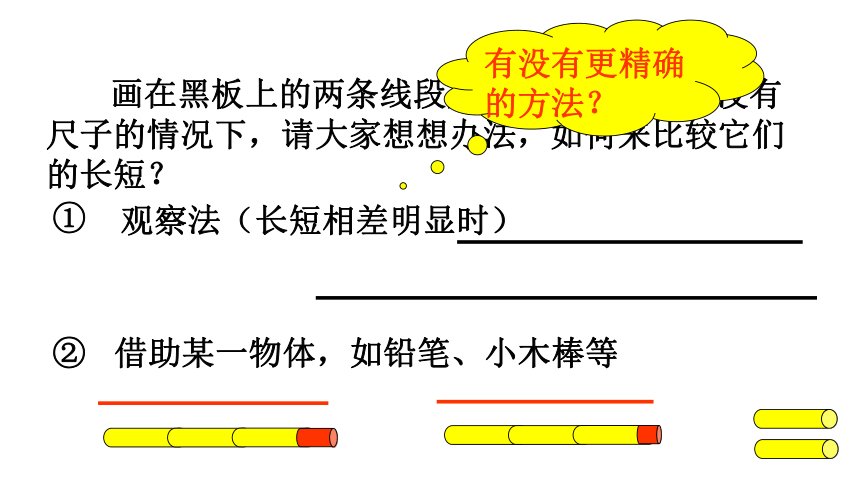
画在黑板上的两条线段是无法移动的,在没有
尺子的情况下,请大家想想办法,如何来比较它们
的长短?
①
观察法(长短相差明显时)
② 借助某一物体,如铅笔、小木棒等
有没有更精确的方法?
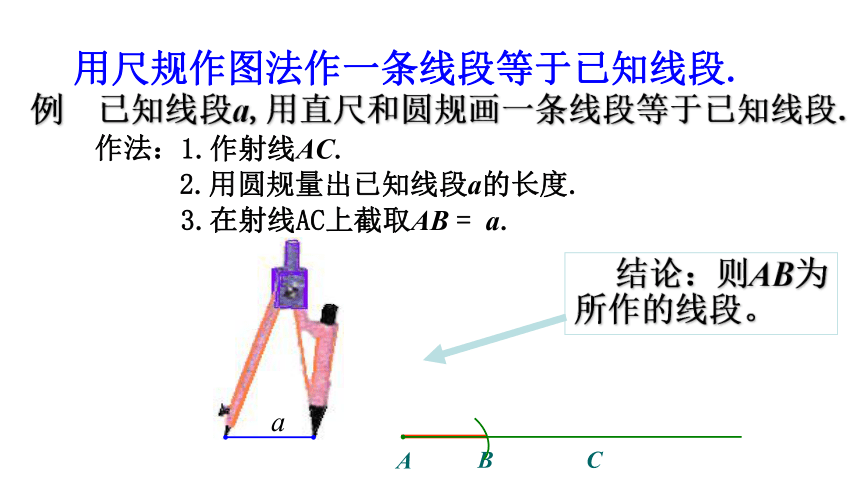
作法:
1.作射线AC.
3.在射线AC上截取AB = a.
结论:则AB为
所作的线段。
2.用圆规量出已知线段a的长度.
用尺规作图法作一条线段等于已知线段.
例 已知线段a,用直尺和圆规画一条线段等于已知线段.
a
A
C
B
思考:(如图)从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能, 在图上画出最短路线.
A
B
怎样走最近呢?
两点间所有连线中,线段最短也可以简单说成:两点之间线段最短.
线段的性质:
实践出真知
A
B
如图,如果量一量你家与学校相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
两点之间线段的长度,叫做这两点之间的距离.
你家
学校
注意: 距离的含义是线段的长度.
典例 · 精析区
以题说法 互动探究
【练习1】 比较下列各线段的长短.
可以借助刻度尺用度量法,也可以借助圆规
用叠合法比较两条线段的长短.
典例 · 精析区
以题说法 互动探究
【练习2】 如图,A、B、C、D为四幢居民楼,现准备建一座超市P,使得超市P到四幢居民楼的距离之和最小,请你设
计符合要求的方案.
解:∵P到A、D的距离之和最小,
∴P在线段AD上,
∵P到C、B的距离之和最小,
∴P在线段CB上.
∵P到A、B、C、D四点的距离之和最小,
∴P应位于线段AD、CB的交点处.(如图)
【拓展1 】在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
A
B
4cm
【拓展2 】在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?其余条件不变,
把B处的蜜糖改成C处,又该如何?
A
B
C
4cm
【拓展3 】在铁丝框的A处有一只蚂蚁,在B、C处各有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?那将“立方体的铁
丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
A
B
C
4cm
【拓展3 】那将“立方体的铁丝框”改成“立方体的纸盒”,
上述两题结论又该如何呢?
A
C
B
C”(C)
C’(C)
4cm
归纳总结
比较线段长短,选用叠合法时,可借助圆规把几条线段移到另一条线段上;选用度量法时,可先用刻度尺度量线段的长度,再按照长度比较它们的长短.
2. 叠合法——从“形”的角度比较;
度量法——从“数值”的角度比较.
3. 要注意两点间的距离指的是线段的长度,是数量,不能说成是“连接两点的线段”,因为线段是图形,不是数量.
4.线段的基本性质:两点之间线段最短.
6.3线段的长短比较
思考:怎样比较两个人的个子高矮?
叠合法
度量法
观察法
方法二:两个人背靠背并立于同一高度地面上
方法一:用测量仪量一下两个人的身高
方法三:直接目测(两个人高矮相差较大时)
第一种方法是:
度量法——即用一把尺量出两条线段的长度,
再进行比较。
3.2cm
4.2cm
线段的比较:
第二种方法是:
叠合法——先把两条线段的一端重合,另一
端落在同侧,根据另一端落下的位置,来比较。
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
观察下列三组图形,你能看出每组图形中线段a与b的长短吗
a
b
a
b
(1)
(3)
(2)
测测眼力吧
观察法不够精确,叠合法比较精确
a
b
画在黑板上的两条线段是无法移动的,在没有
尺子的情况下,请大家想想办法,如何来比较它们
的长短?
①
观察法(长短相差明显时)
② 借助某一物体,如铅笔、小木棒等
有没有更精确的方法?
作法:
1.作射线AC.
3.在射线AC上截取AB = a.
结论:则AB为
所作的线段。
2.用圆规量出已知线段a的长度.
用尺规作图法作一条线段等于已知线段.
例 已知线段a,用直尺和圆规画一条线段等于已知线段.
a
A
C
B
思考:(如图)从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能, 在图上画出最短路线.
A
B
怎样走最近呢?
两点间所有连线中,线段最短也可以简单说成:两点之间线段最短.
线段的性质:
实践出真知
A
B
如图,如果量一量你家与学校相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
两点之间线段的长度,叫做这两点之间的距离.
你家
学校
注意: 距离的含义是线段的长度.
典例 · 精析区
以题说法 互动探究
【练习1】 比较下列各线段的长短.
可以借助刻度尺用度量法,也可以借助圆规
用叠合法比较两条线段的长短.
典例 · 精析区
以题说法 互动探究
【练习2】 如图,A、B、C、D为四幢居民楼,现准备建一座超市P,使得超市P到四幢居民楼的距离之和最小,请你设
计符合要求的方案.
解:∵P到A、D的距离之和最小,
∴P在线段AD上,
∵P到C、B的距离之和最小,
∴P在线段CB上.
∵P到A、B、C、D四点的距离之和最小,
∴P应位于线段AD、CB的交点处.(如图)
【拓展1 】在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
A
B
4cm
【拓展2 】在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?其余条件不变,
把B处的蜜糖改成C处,又该如何?
A
B
C
4cm
【拓展3 】在铁丝框的A处有一只蚂蚁,在B、C处各有一粒蜜糖,
蚂蚁想吃到蜜糖,所走的最短路程是多少cm?那将“立方体的铁
丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
A
B
C
4cm
【拓展3 】那将“立方体的铁丝框”改成“立方体的纸盒”,
上述两题结论又该如何呢?
A
C
B
C”(C)
C’(C)
4cm
归纳总结
比较线段长短,选用叠合法时,可借助圆规把几条线段移到另一条线段上;选用度量法时,可先用刻度尺度量线段的长度,再按照长度比较它们的长短.
2. 叠合法——从“形”的角度比较;
度量法——从“数值”的角度比较.
3. 要注意两点间的距离指的是线段的长度,是数量,不能说成是“连接两点的线段”,因为线段是图形,不是数量.
4.线段的基本性质:两点之间线段最短.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
