浙教版八年级下册 4.1 多边形 课件(共16张PPT)
文档属性
| 名称 | 浙教版八年级下册 4.1 多边形 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 08:00:29 | ||
图片预览

文档简介
(共16张PPT)
4.1多边形(1)
八年级 下册 数学
第4章 平行四边形
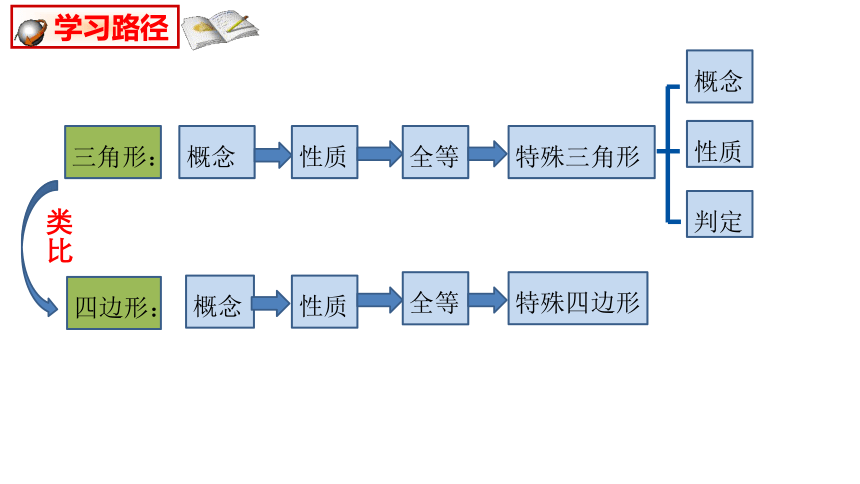
学习路径
三角形:
概念
性质
全等
特殊三角形
四边形:
概念
性质
类比
概念
性质
判定
全等
特殊四边形
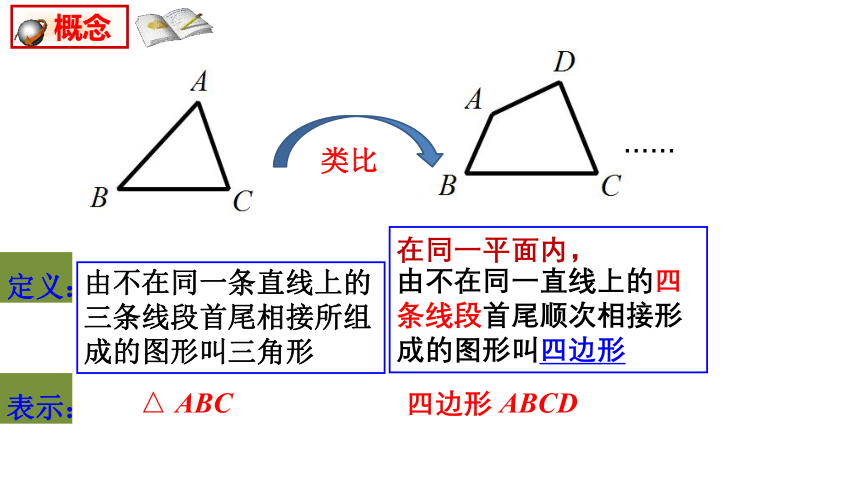
概念
由不在同一条直线上的三条线段首尾相接所组成的图形叫三角形
由不在同一直线上的四条线段首尾顺次相接形成的图形叫四边形
定义:
类比
表示:
△ ABC
四边形 ABCD
……
在同一平面内,
A
B
C
D
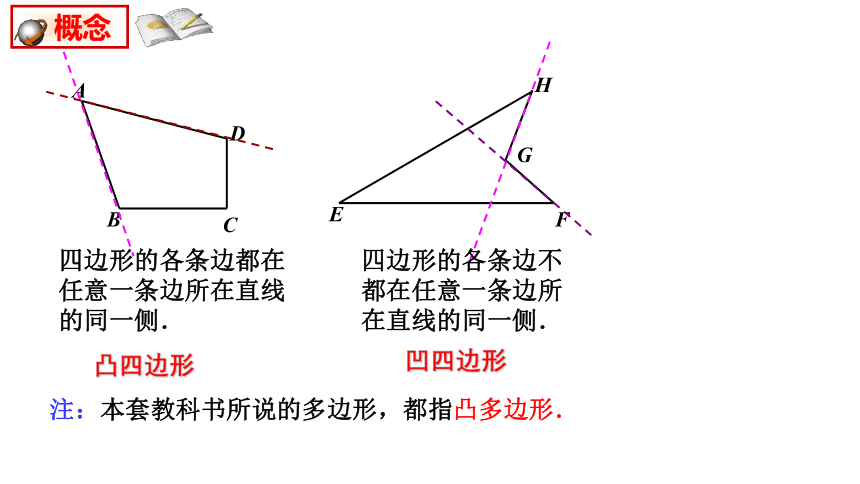
凸四边形
E
F
G
H
凹四边形
注:本套教科书所说的多边形,都指凸多边形.
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
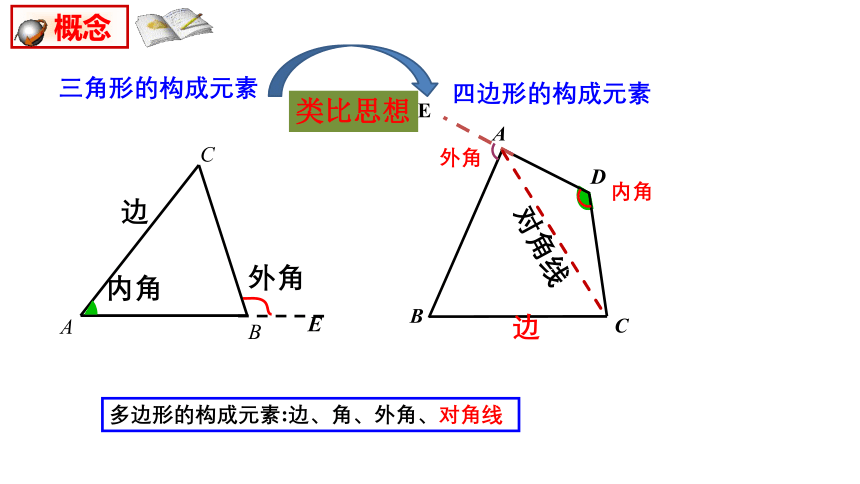
概念
三角形的构成元素
四边形的构成元素
多边形的构成元素:边、角、外角、对角线
类比思想
A
B
C
内角
边
E
外角
A
B
C
D
内角
对角线
外角
E
概念
边
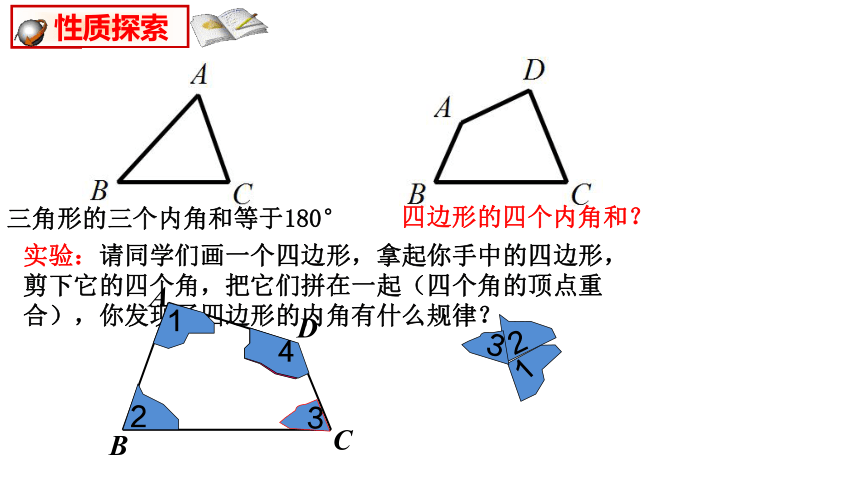
性质探索
三角形的三个内角和等于180°
四边形的四个内角和?
实验:请同学们画一个四边形,拿起你手中的四边形,剪下它的四个角,把它们拼在一起(四个角的顶点重合),你发现了四边形的内角有什么规律?
A
B
C
D
1
2
3
4
1
2
3
4
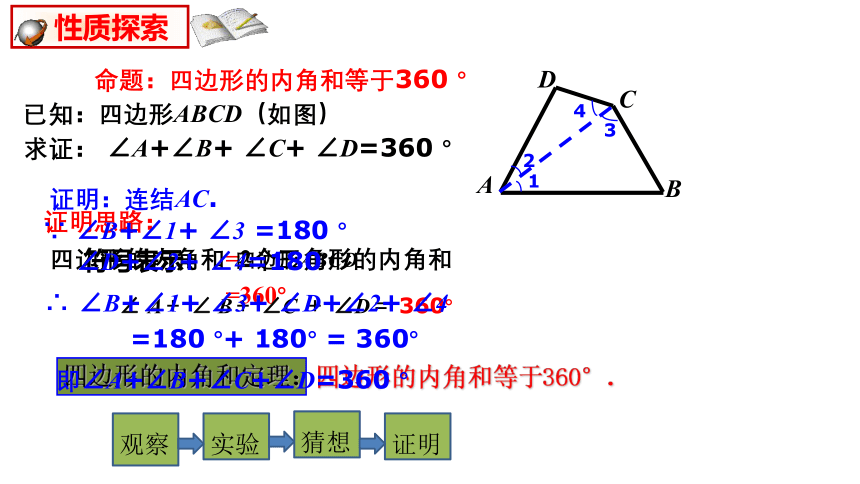
已知:四边形ABCD(如图)
求证: ∠A+∠B+ ∠C+ ∠D=360 °
命题:四边形的内角和等于360 °
性质探索
证明思路:
四边形的内角和=2个三角形的内角和
=360°
符号表示:
四边形ABCD
∠ A+ ∠ B+ ∠C + ∠D= 360°
四边形的内角和等于360°.
四边形的内角和定理:
A
B
C
D
1
2
3
4
证明:连结AC.
∵ ∠B+∠1+ ∠3 =180 °
∠D+∠2+ ∠4=180
∴ ∠B+∠1+ ∠3+ ∠D+∠2+ ∠4
=180 °+ 180° = 360°
即∠A+∠B+∠C+∠D=360 °
观察
实验
猜想
证明
性质探索
你还有其他的证法吗?
四边形
转化思想:
三角形
A
B
C
D
清晨,小明沿一个四边形广场周围的小路,
按逆时针方向跑步。
1
2
3
4
(1)小明在A 处从一条街道转到下一条街道时,
身体转过的角是哪个角?
(2)他跑完一圈,身体旋转了多少度?
(3)在上图中,你能求出 1+ 2+ 3+ 4
的值吗?你是怎样得到的?
四边形的外角和等于360°
1+ 2+ 3+ 4=360 °
性质探索
例1.如图,四边形风筝的四个内角∠A、∠B、
∠C、∠D的度数之比为1∶1∶0.6∶1,求它的
四个内角的度数.
解:
设∠A= x ,则
x+x+0.6x+x=360,
解得x=100
∴ ∠A=∠B= ∠D = 100 ,∠C=60 .
∵ ∠A+∠B+∠C+∠D= 360 (四边形的内角和等于360 ).
又∵ ∠A、∠B、∠C、∠D的
度数之比为1∶1∶0.6∶1,
A
B
C
D
例题精析
方程思想
变式1:如图,四边形风筝的四个内角
∠A=140°, ∠B与∠D互补,
则∠C= .
A
B
C
D
变式2:如图,四边形风筝的四个内角∠B=∠D=90°,∠A:∠C=2:1,
则∠A= .
变式拓展
120°
40°
如图:在四边形ABCD中,
AB=AD=4, ∠A=60 °,
∠ B+∠C=150 °,
BC+CD=8,
求BC和CD的长.
A
D
C
B
4
4
60 °
4
x
拓展提高
1.如图,已知△ABC为直角三角形,
∠C=90°,如果沿图中虚线剪去
∠C,那么∠ 1+∠2=_____ 度。
B
1
2
C
D
E
练习巩固
270
A
如图,在三角形纸片ABC中,将∠A沿DE翻折,使A落在A′处。根据图中所标数据,则
得∠ 1+∠2=_____ 度。
60°
变式拓展
60
课堂梳理
研究路径:
数学知识:
思想方法:
类比
化归
方程
多边形
概念
性质
特殊四边形
四边形内角和定理
四边形外角和定理
四边形及相关概念
感谢你的聆听!
4.1多边形(1)
八年级 下册 数学
第4章 平行四边形
学习路径
三角形:
概念
性质
全等
特殊三角形
四边形:
概念
性质
类比
概念
性质
判定
全等
特殊四边形
概念
由不在同一条直线上的三条线段首尾相接所组成的图形叫三角形
由不在同一直线上的四条线段首尾顺次相接形成的图形叫四边形
定义:
类比
表示:
△ ABC
四边形 ABCD
……
在同一平面内,
A
B
C
D
凸四边形
E
F
G
H
凹四边形
注:本套教科书所说的多边形,都指凸多边形.
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
概念
三角形的构成元素
四边形的构成元素
多边形的构成元素:边、角、外角、对角线
类比思想
A
B
C
内角
边
E
外角
A
B
C
D
内角
对角线
外角
E
概念
边
性质探索
三角形的三个内角和等于180°
四边形的四个内角和?
实验:请同学们画一个四边形,拿起你手中的四边形,剪下它的四个角,把它们拼在一起(四个角的顶点重合),你发现了四边形的内角有什么规律?
A
B
C
D
1
2
3
4
1
2
3
4
已知:四边形ABCD(如图)
求证: ∠A+∠B+ ∠C+ ∠D=360 °
命题:四边形的内角和等于360 °
性质探索
证明思路:
四边形的内角和=2个三角形的内角和
=360°
符号表示:
四边形ABCD
∠ A+ ∠ B+ ∠C + ∠D= 360°
四边形的内角和等于360°.
四边形的内角和定理:
A
B
C
D
1
2
3
4
证明:连结AC.
∵ ∠B+∠1+ ∠3 =180 °
∠D+∠2+ ∠4=180
∴ ∠B+∠1+ ∠3+ ∠D+∠2+ ∠4
=180 °+ 180° = 360°
即∠A+∠B+∠C+∠D=360 °
观察
实验
猜想
证明
性质探索
你还有其他的证法吗?
四边形
转化思想:
三角形
A
B
C
D
清晨,小明沿一个四边形广场周围的小路,
按逆时针方向跑步。
1
2
3
4
(1)小明在A 处从一条街道转到下一条街道时,
身体转过的角是哪个角?
(2)他跑完一圈,身体旋转了多少度?
(3)在上图中,你能求出 1+ 2+ 3+ 4
的值吗?你是怎样得到的?
四边形的外角和等于360°
1+ 2+ 3+ 4=360 °
性质探索
例1.如图,四边形风筝的四个内角∠A、∠B、
∠C、∠D的度数之比为1∶1∶0.6∶1,求它的
四个内角的度数.
解:
设∠A= x ,则
x+x+0.6x+x=360,
解得x=100
∴ ∠A=∠B= ∠D = 100 ,∠C=60 .
∵ ∠A+∠B+∠C+∠D= 360 (四边形的内角和等于360 ).
又∵ ∠A、∠B、∠C、∠D的
度数之比为1∶1∶0.6∶1,
A
B
C
D
例题精析
方程思想
变式1:如图,四边形风筝的四个内角
∠A=140°, ∠B与∠D互补,
则∠C= .
A
B
C
D
变式2:如图,四边形风筝的四个内角∠B=∠D=90°,∠A:∠C=2:1,
则∠A= .
变式拓展
120°
40°
如图:在四边形ABCD中,
AB=AD=4, ∠A=60 °,
∠ B+∠C=150 °,
BC+CD=8,
求BC和CD的长.
A
D
C
B
4
4
60 °
4
x
拓展提高
1.如图,已知△ABC为直角三角形,
∠C=90°,如果沿图中虚线剪去
∠C,那么∠ 1+∠2=_____ 度。
B
1
2
C
D
E
练习巩固
270
A
如图,在三角形纸片ABC中,将∠A沿DE翻折,使A落在A′处。根据图中所标数据,则
得∠ 1+∠2=_____ 度。
60°
变式拓展
60
课堂梳理
研究路径:
数学知识:
思想方法:
类比
化归
方程
多边形
概念
性质
特殊四边形
四边形内角和定理
四边形外角和定理
四边形及相关概念
感谢你的聆听!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
