浙教版九年级上册 3圆的基本性质复习课件(共18张PPT)
文档属性
| 名称 | 浙教版九年级上册 3圆的基本性质复习课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 08:06:48 | ||
图片预览

文档简介
(共18张PPT)
浙教版 数学
九年级(上册)
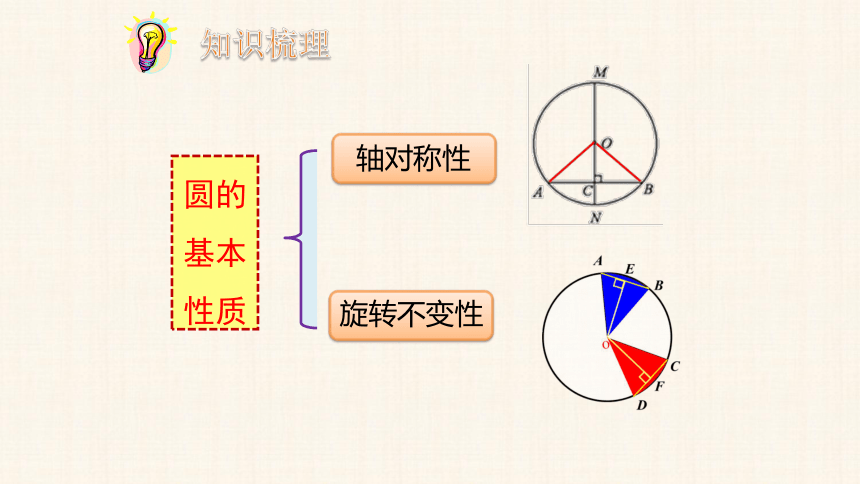
轴对称性
旋转不变性
圆的基本性质
知识梳理
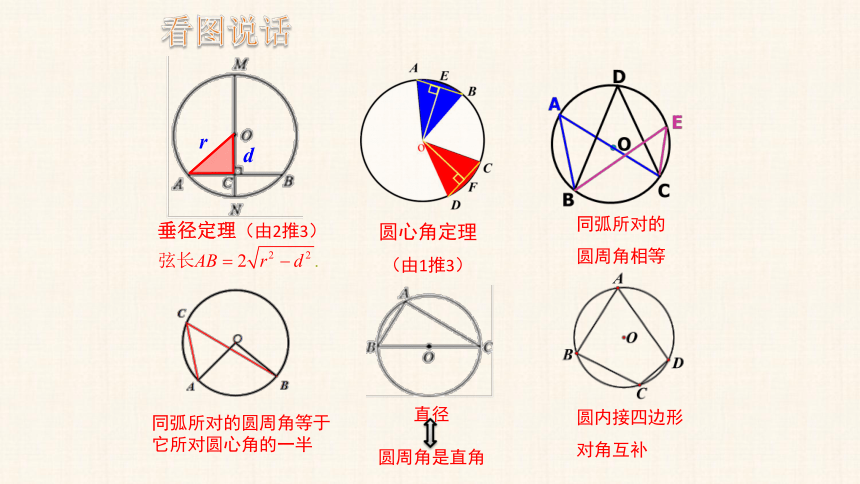
看图说话
垂径定理(由2推3)
r
d
圆心角定理
(由1推3)
同弧所对的
圆周角相等
同弧所对的圆周角等于它所对圆心角的一半
直径
圆周角是直角
圆内接四边形
对角互补
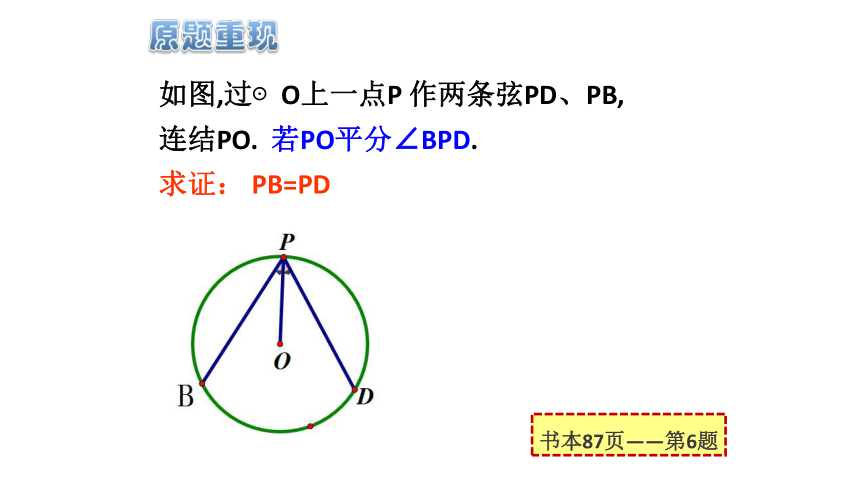
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
书本87页——第6题
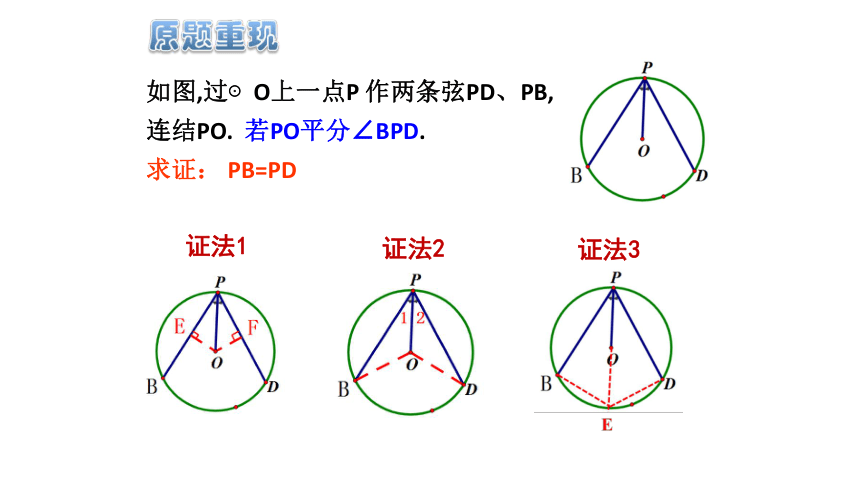
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
证法1
证法2
证法3
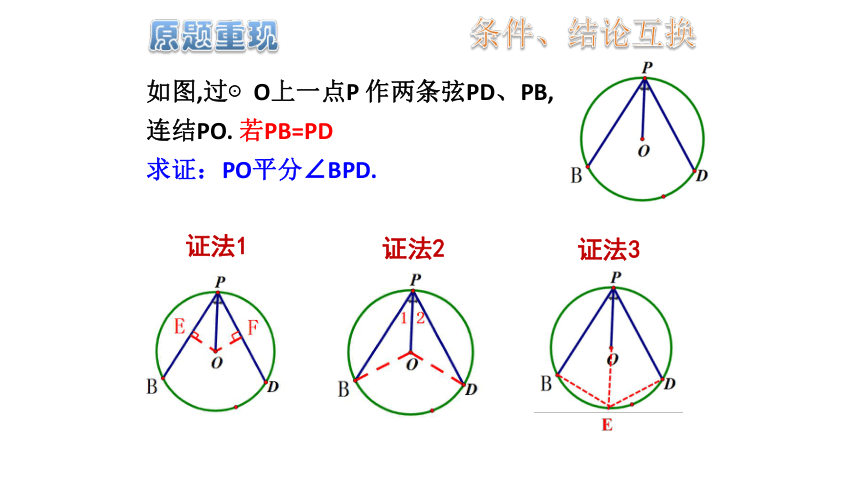
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PB=PD
求证:PO平分∠BPD.
条件、结论互换
证法1
证法2
证法3
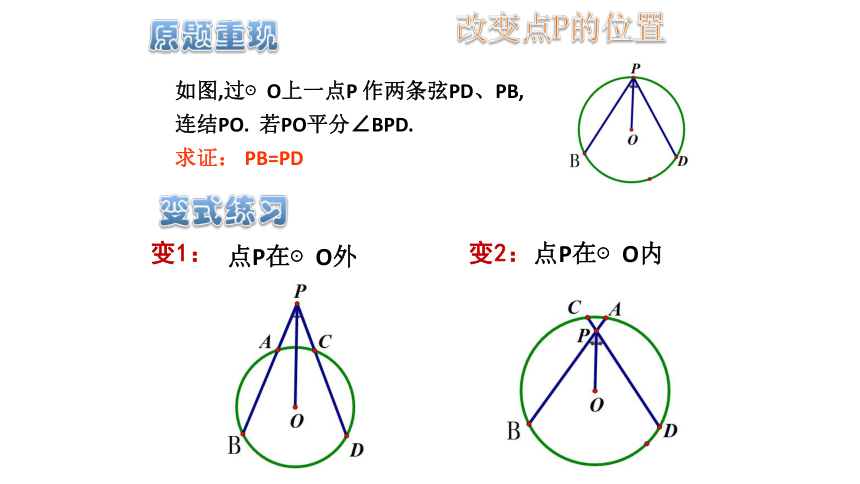
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
变1:
点P在⊙O外
改变点P的位置
变2:
点P在⊙O内
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
变1:
思考:图中还有其他相等的线段吗?
点P在⊙O外,其余条件不变. 求证: PB=PD
改变点P的位置
E
F
如图,过⊙O上一点P 作两条弦PD、PB,
连结OP. 若PO平分∠BPD.
求证: PB=PD
改变点P的位置
变2:
点P在⊙O内,其余条件不变. 求证:PB=PD
E
F
思考:图中还有其他相等的线段吗?
求证: PB=PD
已知:PO平分∠BPD
求证:PO平分∠BPD.
已知:PB=PD
变1:
点P在⊙O外
变2:
点P在⊙O内
变1
变2
模型分析
.
A
C
E
D
1
2
基本图形
当“角平分线”构成的等量关系和“圆”结合的时候,可以转化成“等角、等弧、等弦”互化问题.
B
F
应 用
O
1. 如图,△ABC内接于⊙O,弦AD平分∠BAC,
与BC交于点G,DE⊥AC于E,DF⊥AB于F.
(1)找出图中相等的弦;
(2)求证:△BDG∽△ABD;
(3)求证:EC=BF.
跟踪练习
例题
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径 AB=10 ,弦 AC=6 .
1
2
(1)你能求出哪些线段的长度?
(2)求 的值.
∠ACB=90°
m
n
思考:若直径 AB=m ,弦 AC=n .
则 的值会发生变化吗?
1.如图,⊙O 是△ABC的外接圆,
弦CD平分∠ACB交⊙O于D,连AD,
BD,若直径AB=10,弦AC=6.
思考:求 的值.
变1:
若弦AB=m ,弦AC=n,∠ACB=60°.
变2:
若弦AB=m ,弦AC=n ,∠ACB=2α.
1
2
例题
求 的值.
求 的值.
模型分析
基本图形
应用
一般的,在圆内接三角形中,若出现三角形的内角平分线,那么,角的两边之和与角平分线的比为定值。
跟踪练习
1. 如图,AB是⊙0的直径,弦AC长为4a,
弦BC长为5a,∠ACB的平分线交⊙0于点D,
则CD的长为 .
2. 如图,点O1在x轴正半轴上,⊙O1交x轴于C,D两点,
交y轴于A,B两点,OC=1,OA= .
跟踪练习
小 结
O
求证: PB=PD
已知:PO平分∠BPD
圆+
角平分线
浙教版 数学
九年级(上册)
轴对称性
旋转不变性
圆的基本性质
知识梳理
看图说话
垂径定理(由2推3)
r
d
圆心角定理
(由1推3)
同弧所对的
圆周角相等
同弧所对的圆周角等于它所对圆心角的一半
直径
圆周角是直角
圆内接四边形
对角互补
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
书本87页——第6题
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
证法1
证法2
证法3
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PB=PD
求证:PO平分∠BPD.
条件、结论互换
证法1
证法2
证法3
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
变1:
点P在⊙O外
改变点P的位置
变2:
点P在⊙O内
如图,过⊙O上一点P 作两条弦PD、PB,
连结PO. 若PO平分∠BPD.
求证: PB=PD
变1:
思考:图中还有其他相等的线段吗?
点P在⊙O外,其余条件不变. 求证: PB=PD
改变点P的位置
E
F
如图,过⊙O上一点P 作两条弦PD、PB,
连结OP. 若PO平分∠BPD.
求证: PB=PD
改变点P的位置
变2:
点P在⊙O内,其余条件不变. 求证:PB=PD
E
F
思考:图中还有其他相等的线段吗?
求证: PB=PD
已知:PO平分∠BPD
求证:PO平分∠BPD.
已知:PB=PD
变1:
点P在⊙O外
变2:
点P在⊙O内
变1
变2
模型分析
.
A
C
E
D
1
2
基本图形
当“角平分线”构成的等量关系和“圆”结合的时候,可以转化成“等角、等弧、等弦”互化问题.
B
F
应 用
O
1. 如图,△ABC内接于⊙O,弦AD平分∠BAC,
与BC交于点G,DE⊥AC于E,DF⊥AB于F.
(1)找出图中相等的弦;
(2)求证:△BDG∽△ABD;
(3)求证:EC=BF.
跟踪练习
例题
1.如图,⊙O 是△ABC的外接圆,弦CD平分∠ACB交⊙O于D,连AD,BD,若直径 AB=10 ,弦 AC=6 .
1
2
(1)你能求出哪些线段的长度?
(2)求 的值.
∠ACB=90°
m
n
思考:若直径 AB=m ,弦 AC=n .
则 的值会发生变化吗?
1.如图,⊙O 是△ABC的外接圆,
弦CD平分∠ACB交⊙O于D,连AD,
BD,若直径AB=10,弦AC=6.
思考:求 的值.
变1:
若弦AB=m ,弦AC=n,∠ACB=60°.
变2:
若弦AB=m ,弦AC=n ,∠ACB=2α.
1
2
例题
求 的值.
求 的值.
模型分析
基本图形
应用
一般的,在圆内接三角形中,若出现三角形的内角平分线,那么,角的两边之和与角平分线的比为定值。
跟踪练习
1. 如图,AB是⊙0的直径,弦AC长为4a,
弦BC长为5a,∠ACB的平分线交⊙0于点D,
则CD的长为 .
2. 如图,点O1在x轴正半轴上,⊙O1交x轴于C,D两点,
交y轴于A,B两点,OC=1,OA= .
跟踪练习
小 结
O
求证: PB=PD
已知:PO平分∠BPD
圆+
角平分线
同课章节目录
