【专题训练】二次函数性质分类练习 (含解析)
文档属性
| 名称 | 【专题训练】二次函数性质分类练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 17:17:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数性质分类练习
一、二次函数性质——对称性比较大小
1.已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( )
A. 2>y1>y2 B. 2>y2 >y1 C. y1>y2>2 D. y2 >y1>2
2.已知两点A(-6,y1),B(2,y2)均在抛物线y=ax2+bx+c(a>0)上,若y1>y2 , 则抛物线的顶点横坐标m的值可以是( )
A. -6 B. -5 C. -2 D. -1
3.已知点A(a-m , y1)、B(a-n , y2)、C(a+b , y3)都在二次函数y=x2-2ax +1的图象上,若0A. y1< y2< y3 B. y1 < y3< y2 C. y3< y1< y2 D. y2< y3< y1
4.已知抛物线 (m是常数),点A( , ),B( , )在抛物线上,若 , ,则m,y1 , y2的大小关系的是( )
A. B. C. D.
5.若点M(﹣1,y1),N(1,y2),P( )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y1<y2 D. 2<y1<y3
6.如果点A(-2,y1)和点B(2,y2)是抛物线y=(x+3)2上的两点,那么 y1________y2(填“>”“=”或“<”).
二、二次函数性质——增减性
7.在二次函数 的图像中,若 随 的增大而增大,则 的取值范围是( )
A. B. C. D.
8.对于二次函数y=﹣x2﹣4x+5,以下说法正确的是( )
A. x<﹣1时,y随x的增大而增大 B. x<﹣5或x>1时,y>0
C. A(﹣4,y1),B( ,y2)在y=﹣x2﹣4x+5的图象上,则y1<y2 D. 此二次函数的最大值为8
9.已知二次函数 (k为常数,且k > 0),当x < m时,y随着x的增大而增大,则满足条件的整数m的值为________.(写出一个即可)
x … ﹣1 0 1 2 …
y … 0 3 4 3 …
10.已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示:
那么它的图象与x轴的另一个交点坐标是( )
A. (1,4) B. (2,0) C. (3,0) D. (4,0)
x … -5 -4 -3 -2 -1 0 …
y … 4 0 -2 -2 0 4 …
11.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法:①抛物线的开口向下;②当x>-3时,y随x的增大而增大;③二次函数的最小值是-2;④抛物线的对称轴是x=-2.5.其中正确的是________.(填序号)
三、二次函数性质——系数之间的关系
12.已知二次函数y=ax2+bx+c的图象大致如图所示,则下列关系式中成立的是( )
A. a>0 B. b<0 C. c<0 D. b+2a>0
13.二次函数y=ax2+bx+c(a≠0)的图象如图
下列结论:(1)c<0;(2)b>0;(3)4a+2b+c>0;(4)(a+c)2其中不正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
14.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
15.抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
16.如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3③a+b+c>0④当x>1时,y随x的增大而增大.正确的说法有________.
17.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0 ②b<0 ③c>0 ④4a+2b+c=0, ⑤b+2a=0 ⑥ b2-4ac>0其中正确的是________.(写出所有正确结论的序号)
18.如图,抛物线 (a≠0)的对称轴为直x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程 =0的两个根是 ③ ;④当 时,x的取值范围是 ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
19.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y )在该抛物线上,则y>y .其中正确的结论有________ .(写出所有正确结论的序号)
四、二次函数性质——最值
20.关于二次函数 的最大值或最小值,下列说法正确的是( )
A. 有最大值4 B. 有最小值4 C. 有最大值6 D. 有最小值6
21.当 时,二次函数 有( )
A. 最大值-3 B. 最小值-3 C. 最大值-4 D. 最小值-4
22.已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A. 有最大值﹣1,有最小值﹣2 B. 有最大值0,有最小值﹣1
C. 有最大值7,有最小值﹣1 D. 有最大值7,有最小值﹣2
23.已知二次函数 (其中 是自变量),当 时, 随 的增大而减小,且 时, 的最小值为15,则 的值为( )
A. 1或-2 B. 或 C. -2 D. 1
24.已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )
A. 16 B. 15 C. 9 D. 7
25.已知二次函数 ,当0≤x≤4,y的最小值是________,最大值是________.
26.已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为________.
答案解析部分
一、二次函数性质——对称性比较大小
1.【答案】 A
【解析】【解答】解:∵ y=-(x+1)2+2的顶点坐标为(-1,2),对称轴是直线x=-1,二次项系数a<0,
∴当x=-1的时候函数有最大值y=2,当x>-1的时候y随x的增大而减小,
∵ A(1,y1),B(2,y2)
∴2>1>-1,
∴ 2>y1>y2 。
故答案为:A。
【分析】根据二次函数的解析式的性质与系数的关系得出:当x=-1的时候函数有最大值y=2,当x>-1的时候y随x的增大而减小,从而根据A,B两点的横坐标即可判断得出答案。
2.【答案】 D
【解析】【解答】解:假设点A(-6,y1),B(2,y2)是抛物线y=ax2+bx+c(a>0)的两个对称点,
∴对称轴为直线x=;
∵ y1>y2 ,
∴抛物线的开口向上,抛物线上的点离对称轴越近,y的值越小,
∴该抛物线的顶点的横坐标m>-2,
∴选项中m=-1.
故答案为:D.
【分析】假设点A(-6,y1),B(2,y2)是抛物线y=ax2+bx+c(a>0)的两个对称点,可求出抛物线的对称轴,再根据y1>y2 , 可得到抛物线的开口向上,抛物线上的点离对称轴越近,y的值越小,由此可求出顶点横坐标的取值范围,根据各选项,可得答案.
3.【答案】 B
【解析】【解答】解:∵y=x2-2ax +1
∴对称轴为x=a
点A、B的情况:n>m,故点B比点A离对称轴远,故y2>y1;
点A、C的情况:my1;
点B,C的情况:by3;
∴故y1故答案为B.
【分析】先确定二次函数图象的对称轴,然后运用二次函数的性质进行解答即可.
4.【答案】 A
【解析】【解答】∵ ,
∴ ,有最大值为 ,
∴抛物线开口向下,
∵抛物线 对称轴为直线 ,
设A( , )的对称点为A′( , ),
∴
∴ ,
∵ , ,
∴ ,
∴ .
故答案为:A.
【分析】根据二次函数的性质得到抛物线 的开口向下,有最大值为 ,对称轴为直线 ,设A( , )的对称点为A′( , ),从而求得 ,由 , ,得出 ,则在对称轴右侧,y随x的增大而减小,所以 时, .
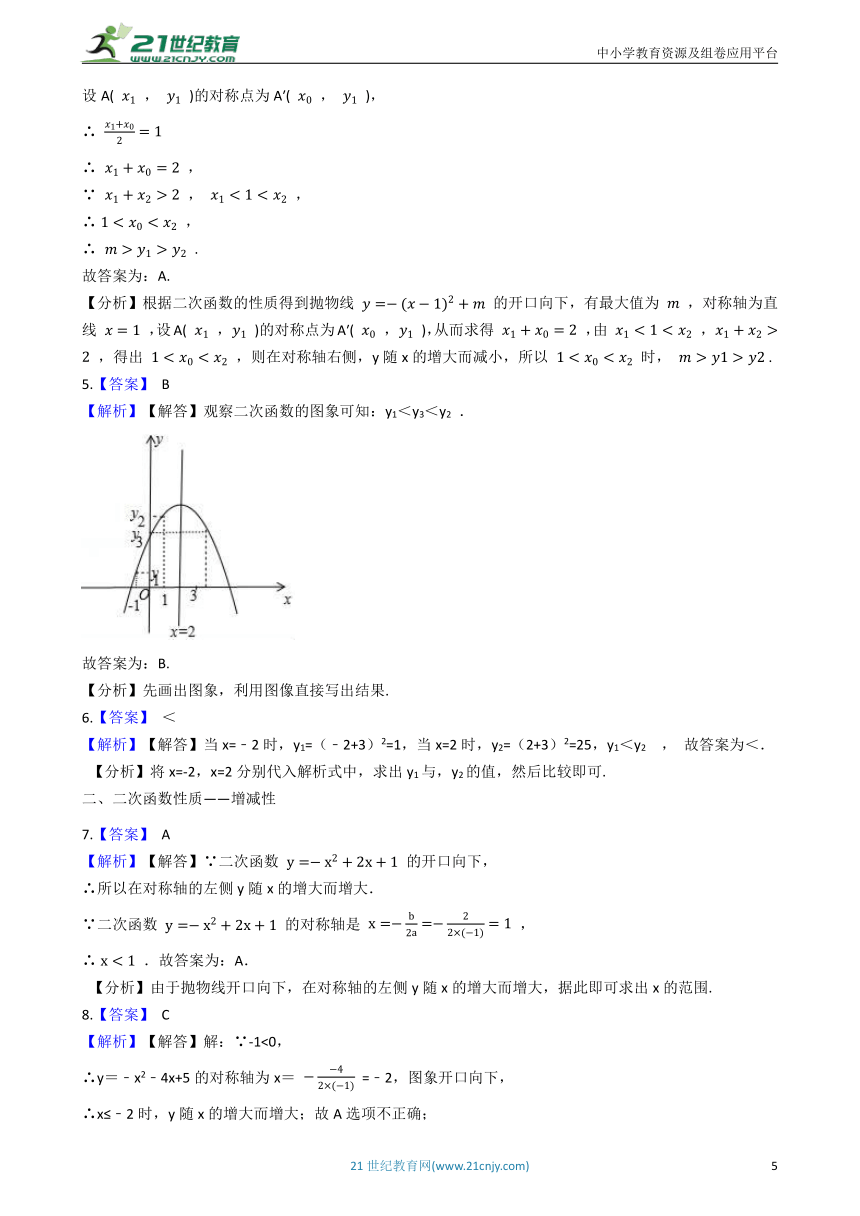
5.【答案】 B
【解析】【解答】观察二次函数的图象可知:y1<y3<y2 .
故答案为:B.
【分析】先画出图象,利用图像直接写出结果.
6.【答案】 <
【解析】【解答】当x=﹣2时,y1=(﹣2+3)2=1,当x=2时,y2=(2+3)2=25,y1<y2 , 故答案为<.
【分析】将x=-2,x=2分别代入解析式中,求出y1与,y2的值,然后比较即可.
二、二次函数性质——增减性
7.【答案】 A
【解析】【解答】∵二次函数 的开口向下,
∴所以在对称轴的左侧y随x的增大而增大.
∵二次函数 的对称轴是 ,
∴ .故答案为:A.
【分析】由于抛物线开口向下,在对称轴的左侧y随x的增大而增大,据此即可求出x的范围.
8.【答案】 C
【解析】【解答】解:∵-1<0,
∴y=﹣x2﹣4x+5的对称轴为x= =﹣2,图象开口向下,
∴x≤﹣2时,y随x的增大而增大;故A选项不正确;
∵﹣x2﹣4x+5=0时的两个根为x=﹣5,x=1,
∴当﹣5<x<1时,y>0;故B选项不正确;
∵-2-(﹣4)>﹣ -(﹣2),
∴点A到对称轴的距离大于点B到对称轴的距离,
∴y1<y2;故C选项正确;
当x=﹣2时,y有最大值9,故D选项不正确.
故答案为:C.
【分析】首先求出二次函数的对称轴,然后判断出单调性,据此可判断选项A;求出二次函数所对应的一元二次方程的两根,然后根据单调性可判断选项B;根据二次函数的单调性可判断选项C;由于二次函数开口向下,故在对称轴处取得最大值,据此可判断D.
9.【答案】 m=-2(不唯一,m为不大于-2的整数)
【解析】【解答】解:k > 0,-k<0,抛物线开口向下,
抛物线对称轴 ,
在对称轴的左侧,y随x增大而增大,
∵ ,
∴ ,
∴ ,
∵m为整数 ,
∴m=-2(不唯一).
故m=-2(不唯一,m为不大于-2的整数).
【分析】由二次函数的对称轴可得抛物线对称轴,根据抛物线开口朝下,且 当x < m时,y随着x的增大而增大可得对称轴≤m,由 k > 0 可得m范围,即可找到符合题意的值.
10.【答案】 C
【解析】【解答】∵抛物线y=ax2+bx+c经过(0,3)、(2,3)两点,∴对称轴x 1;
点(﹣1,0)关于对称轴对称点为(3,0),因此它的图象与x轴的另一个交点坐标是(3,0).
故答案为:C.
【分析】根据(0,3)、(2,3)两点求得对称轴,再利用对称性解答即可.
11.【答案】 ④
【解析】【解答】解:由题意可知函数图象过点 、 和 ,
,解得 ,
抛物线解析式为 ,
抛物线开口向上,对称轴为 ,最小值为 ,当 时 随 的增大而增大,
正确的是④,
故答案为:④.
【分析】首先根据表格提供的数据,利用待定系数法求出抛物线的解析式,然后将抛物线的解析式配成顶点式,根据抛物线的系数、图象与性质即可一一判断得出答案。
三、二次函数性质——系数之间的关系
12.【答案】 D
【解析】【解答】∵抛物线开口向下,对称轴大于1,与y轴交于正半轴,∴a<0,﹣ >1,c>0,∴b>﹣2a,∴b+2a>0.
故答案为:D.
【分析】由抛物线开口向下知a<0,由抛物线的对称轴直线大于1,得出b>﹣2a,b>0,即b+2a>0,由抛物线与y轴的交点在y轴的正半轴,得出c>0.
13.【答案】 C
【解析】【解答】抛物线的开口向上,则a>0;
对称轴为x=﹣ =1,即b=﹣2a,故b<0,故(2)错误;
抛物线交y轴于负半轴,则c<0,故(1)正确;
把x=2代入y=ax2+bx+c得:y=4a+2b+c<0,故(3)错误;
把x=1代入y=ax2+bx+c得:y=a+b+c<0,把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c<0,
则(a+b+c)(a﹣b+c)>0,故(4)错误;
不正确的是(2)(3)(4);
故答案为:C.
【分析】根据抛物线的开口方向可判断a的符号,根据抛物线与y轴的交点可得出c值,再根据图象经过的点的情况进行推理,即可对结论进行判断。
14.【答案】 D
【解析】【解答】根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
对称轴:x= >0,
①∵它与x轴的两个交点分别为( 1,0),(3,0),
∴对称轴是x=1,
∴ =1,
∴b+2a=0,
故①正确;
②∵a>0, =1,
∴b<0,
又∵c<0,
∴abc>0,
故②错误;
③∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,
由①知,b= 2a,
∴8a+c>0;
故④正确;
综上所述,正确的结论是:①③④,
故答案为:D.
【分析】根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,对称轴在y轴的右侧,则a,b异号,故b<0,abc>0;由根据抛物线的对称性及与x轴两个交点的坐标得出其对称轴直线是x=1,故b+2a=0;由抛物线与x轴有两个交点,故b2﹣4ac>0;根据图示知,当x=4时,y>0,即16a+4b+c>0,故8a+c>0。
15.【答案】 C
【解析】【解答】①∵抛物线开口向下,
抛物线对称轴位于y轴的左侧,则a、b同号,故ab>0,
抛物线与y轴交于负半轴,则c<0,故abc<0,
故①正确;
②∵抛物线开口方向向下,
∴a<0,
∵x=- =h,且-2<h<-1,
∴4a<b<2a,
∴4a-b<0,
又∵h<0,
∴- <1
∴2a+b<0,
∴(4a-b)(2a+b)>0,
故②错误;
③由②知:b>4a,
∴2b-8a>0①.
当x=-2时,4a-2b+c>0②,
由①+②得:4a-8a+c>0,即4a-c<0.
故③正确;
④∵当x=-1时,a-b+c>0,
∵OC=OB,
∴当x=c时,y=0,即ac2+bc+c=0,
∵c≠0,
∴ac+b+1=0,
∴ac=-b-1,
则(a+1)(c+1)=ac+a+c+1=-b-1+a+c+1=a-b+c>0,
故④正确;
所以本题正确的有:①③④,
故答案为:C.
【分析】由抛物线开口向下,知a<0,抛物线对称轴位于y轴的左侧,则a、b同号,故,b<0,抛物线与y轴交于负半轴,则c<0;由抛物线的对称轴直线-2<h<-1,根据对称轴公式及不等式的性质得出4a<b<2a,进而得出4a-b<0,2a+b<0,故(4a-b)(2a+b)>0;由于b>4a,根据不等式的性质得出2b-8a>0,又当x=-2时,4a-2b+c>0,故4a-8a+c>0,即4a-c<0;当x=-1时,a-b+c>0,又OC=OB,当x=c时,y=0,即ac2+bc+c=0,根据等式的性质得出ac+b+1=0,即ac=-b-1,故(a+1)(c+1)=ac+a+c+1=-b-1+a+c+1=a-b+c>0。
16.【答案】 ①②③
【解析】【解答】∵抛物线的开口向下,
∵与y轴的交点为在y轴的正半轴上,
故①正确;
∵对称轴为x=1抛物线与x轴的一个交点为
∴另一个交点为
∴方程 的根是
故②正确;
当x=1时,
故③正确;
a,b异号,即
当 时,y随x的增大而减小,故④错误.
∴其中正确的说法有①②③;
故答案为:①②③.
【分析】由抛物线的开口向下,知a < 0 ,由抛物线与y轴的交点在y轴的正半轴上,知c > 0 ,故a c < 0 ;对称轴直线及抛物线与x轴的一个交点,由抛物线的对称轴性即可得出抛物线与x轴的另一个交点的坐标,由抛物线与x轴的交点坐标即可得出方程 ax2+bx+c=0 的根;当x=1时, y=a+b+c>0 ,当x>1时,图像从左至右下降,故y随x的增大而减小.
17.【答案】 ①③⑤⑥
【解析】【解答】①如图,抛物线开口方向向下,则a<0.故①正确;
②如图,抛物线对称轴x=- =1,则b=-2a>0.即b>0,故②错误;
③如图,抛物线与y轴交于正半轴,则c>0,故③正确;
④如图,当x=2时,y>0,即4a+2b+c>0,故④错误;
⑤由抛物线对称轴x=- =1得到b+2a=0.故⑤正确;
⑥如图,抛物线与x轴有2个交点,则b2-4ac>0,故⑥正确;
综上所述,正确的结论是①③⑤⑥
【分析】由抛物线开口方向向下,知a<0;由抛物线的对称轴直线是x=1得出b=-2a>0.即b>0,b+2a=0;由抛物线与y轴交于正半轴,知c>0;由图像知:当x=2时,y>0,即4a+2b+c>0;由抛物线与x轴有2个交点,知:b2-4ac>0,综上所述即可得出答案。
18.【答案】 C
【解析】【解答】∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以②正确;
∵x=- =1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,所以③错误;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,故当x1<x2<0时,y1<y2.所以⑤正确.
故答案为①②⑤.
【分析】由抛物线与x轴有2个交点,知b2-4ac>0;由抛物线的对称轴直线及抛物线与x轴一个交点的坐标,即可判断出抛物线与x轴的另一个交点的坐标,根据抛物线与x轴交点的纵坐标即可知道方程ax2+bx+c=0的根的情况;由对称轴直线是x=1得出b=-2a,而x=-1时,y=0,即a-b+c=0,故a+2a+c=0;由于自变量的取值在-1<x<3时,图像位于x轴的上方,故对应的函数值大于0,即y>0;由图像知:当x<1时,图像从左至右上升,此时y随x增大而增大,故当x1<x2<0时,y1<y2。
19.【答案】 ①②④⑤
【解析】【解答】抛物线与y轴交于原点,c=0,故①正确;
该抛物线的对称轴是: ,直线x=﹣1,故②正确;
当x=1时,y=a+b+c
∵对称轴是直线x=﹣1,∴﹣b/2a=﹣1,b=2a.又∵c=0,∴y=3a,故③错误;
x=m对应的函数值为y=am2+bm+c,x=﹣1对应的函数值为y=a﹣b+c.又∵x=﹣1时函数取得最小值,∴a﹣b+c<am2+bm+c,即a﹣b<am2+bm.∵b=2a,∴am2+bm+a>0(m≠﹣1).故④正确.∵|100+1|>|﹣100+1|,且开口向上,∴y1>y2 . 故⑤正确.
故答案为:①②④⑤.
【分析】根据抛物线与y轴的交点判断c和0的关系,再根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断。
四、二次函数性质——最值
20.【答案】 D
【解析】【解答】解:∵在二次函数 中,a=2>0,顶点坐标为(4,6),
∴函数有最小值为6.
故答案为:D.
【分析】该二次函数表达式为顶点式,由于张口向上,即可得出函数有最小值,结合顶点坐标即可解答.
21.【答案】 B
【解析】【解答】解:∵二次函数 ,
∴抛物线的对称轴为:x=1,
∵函数开口向上,
∴当x≥2时,y随x的增大而增大,
∴当x=2时,y最小值=(2-1)2-4=-3
故答案为:B
【分析】根据二次函数y=(x-1)2-4,可以得到当x>1时,该函数有最小值,故可得结论.
22.【答案】 D
【解析】【解答】∵由 知当x=2,最小值为-2,又∵x=-1与x=3关于x=2对称故最大值为 ,
故答案为:D。
【分析】先配方,∵对称轴x=2,在给定定义域范围内,故最小值可求。图像张口向上,故离图像最远的点为最大值。
23.【答案】 C
【解析】【解答】解:∵ ,
∴该抛物线的对称轴是直线x=﹣1,
∵当 时, 随 的增大而减小,
∴a<0,
∵当 时, 的最小值为15,
∴当x=1时,y=15,
即 ,解得: ,
∵a<0,∴a=﹣2.
故答案为:C.
【分析】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向下a<0,再由 时, 的最小值为15,可得当x=1时,y=15,即可求得a。
24.【答案】 D
【解析】【解答】解:∵a+b=3,c﹣3a=-6,
∴b=3﹣a,c=3a-6.
∵b,c都是非负数,
∴ ,
解不等式①得:a≤3,
解不等式②得:a≥ ,
∴2≤a≤3.
又∵a是非负数,
∴2≤a≤3,
S=a2+b+c=a2+(3﹣a)+3a-6=a2+2a-3,
∴对称轴为直线a=﹣ =﹣1,
∴a=2时,最小值n=5,
∴a=3时,最大值m=32+2×3-3=12,
∴m﹣n=12﹣5=7.
故答案为:D.
【分析】用a表示出b、c并求出a的取值范围,再代入S整理成关于a的函数形式,然后根据二次函数的增减性求出m、n的值,再相减即可得解.
25.【答案】 -1;8
【解析】【解答】由二次函数公式可得:对称轴为直线x=3;
x=3在0≤x≤4范围内,故x=3时,函数有最小值-1.
当x=0时,函数取到最大值8.
【分析】根据x=-可求得对称轴方程;结合已知和二次函数的性质可得函数有最小值-1;根据x的范围可知当x=0时,函数取到最大值8.
26.【答案】 1
【解析】【解答】解:∵二次函数y=ax2+2ax+3a2+3(其中x是自变量),
∴对称轴是直线x= = 1,
∵当x≥2时,y随x的增大而增大,
∴a>0,
∵ 2≤x≤1时,y的最大值为9,
∴x=1时,y=a+2a+3a2+3=9,
∴3a2+3a 6=0,
∴a=1,或a= 2(不合题意舍去).
故答案为1.
【分析】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向上a>0,然后由 2≤x≤1时,y的最大值为9,可得x=1时,y=9,即可求出a.
21世纪教育网(www.21cnjy.com)
二次函数性质分类练习
一、二次函数性质——对称性比较大小
1.已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( )
A. 2>y1>y2 B. 2>y2 >y1 C. y1>y2>2 D. y2 >y1>2
2.已知两点A(-6,y1),B(2,y2)均在抛物线y=ax2+bx+c(a>0)上,若y1>y2 , 则抛物线的顶点横坐标m的值可以是( )
A. -6 B. -5 C. -2 D. -1
3.已知点A(a-m , y1)、B(a-n , y2)、C(a+b , y3)都在二次函数y=x2-2ax +1的图象上,若0
4.已知抛物线 (m是常数),点A( , ),B( , )在抛物线上,若 , ,则m,y1 , y2的大小关系的是( )
A. B. C. D.
5.若点M(﹣1,y1),N(1,y2),P( )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y1<y2 D. 2<y1<y3
6.如果点A(-2,y1)和点B(2,y2)是抛物线y=(x+3)2上的两点,那么 y1________y2(填“>”“=”或“<”).
二、二次函数性质——增减性
7.在二次函数 的图像中,若 随 的增大而增大,则 的取值范围是( )
A. B. C. D.
8.对于二次函数y=﹣x2﹣4x+5,以下说法正确的是( )
A. x<﹣1时,y随x的增大而增大 B. x<﹣5或x>1时,y>0
C. A(﹣4,y1),B( ,y2)在y=﹣x2﹣4x+5的图象上,则y1<y2 D. 此二次函数的最大值为8
9.已知二次函数 (k为常数,且k > 0),当x < m时,y随着x的增大而增大,则满足条件的整数m的值为________.(写出一个即可)
x … ﹣1 0 1 2 …
y … 0 3 4 3 …
10.已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示:
那么它的图象与x轴的另一个交点坐标是( )
A. (1,4) B. (2,0) C. (3,0) D. (4,0)
x … -5 -4 -3 -2 -1 0 …
y … 4 0 -2 -2 0 4 …
11.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法:①抛物线的开口向下;②当x>-3时,y随x的增大而增大;③二次函数的最小值是-2;④抛物线的对称轴是x=-2.5.其中正确的是________.(填序号)
三、二次函数性质——系数之间的关系
12.已知二次函数y=ax2+bx+c的图象大致如图所示,则下列关系式中成立的是( )
A. a>0 B. b<0 C. c<0 D. b+2a>0
13.二次函数y=ax2+bx+c(a≠0)的图象如图
下列结论:(1)c<0;(2)b>0;(3)4a+2b+c>0;(4)(a+c)2
A. 1个 B. 2个 C. 3个 D. 4个
14.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
15.抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
16.如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3③a+b+c>0④当x>1时,y随x的增大而增大.正确的说法有________.
17.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0 ②b<0 ③c>0 ④4a+2b+c=0, ⑤b+2a=0 ⑥ b2-4ac>0其中正确的是________.(写出所有正确结论的序号)
18.如图,抛物线 (a≠0)的对称轴为直x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程 =0的两个根是 ③ ;④当 时,x的取值范围是 ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
19.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y )在该抛物线上,则y>y .其中正确的结论有________ .(写出所有正确结论的序号)
四、二次函数性质——最值
20.关于二次函数 的最大值或最小值,下列说法正确的是( )
A. 有最大值4 B. 有最小值4 C. 有最大值6 D. 有最小值6
21.当 时,二次函数 有( )
A. 最大值-3 B. 最小值-3 C. 最大值-4 D. 最小值-4
22.已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A. 有最大值﹣1,有最小值﹣2 B. 有最大值0,有最小值﹣1
C. 有最大值7,有最小值﹣1 D. 有最大值7,有最小值﹣2
23.已知二次函数 (其中 是自变量),当 时, 随 的增大而减小,且 时, 的最小值为15,则 的值为( )
A. 1或-2 B. 或 C. -2 D. 1
24.已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )
A. 16 B. 15 C. 9 D. 7
25.已知二次函数 ,当0≤x≤4,y的最小值是________,最大值是________.
26.已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为________.
答案解析部分
一、二次函数性质——对称性比较大小
1.【答案】 A
【解析】【解答】解:∵ y=-(x+1)2+2的顶点坐标为(-1,2),对称轴是直线x=-1,二次项系数a<0,
∴当x=-1的时候函数有最大值y=2,当x>-1的时候y随x的增大而减小,
∵ A(1,y1),B(2,y2)
∴2>1>-1,
∴ 2>y1>y2 。
故答案为:A。
【分析】根据二次函数的解析式的性质与系数的关系得出:当x=-1的时候函数有最大值y=2,当x>-1的时候y随x的增大而减小,从而根据A,B两点的横坐标即可判断得出答案。
2.【答案】 D
【解析】【解答】解:假设点A(-6,y1),B(2,y2)是抛物线y=ax2+bx+c(a>0)的两个对称点,
∴对称轴为直线x=;
∵ y1>y2 ,
∴抛物线的开口向上,抛物线上的点离对称轴越近,y的值越小,
∴该抛物线的顶点的横坐标m>-2,
∴选项中m=-1.
故答案为:D.
【分析】假设点A(-6,y1),B(2,y2)是抛物线y=ax2+bx+c(a>0)的两个对称点,可求出抛物线的对称轴,再根据y1>y2 , 可得到抛物线的开口向上,抛物线上的点离对称轴越近,y的值越小,由此可求出顶点横坐标的取值范围,根据各选项,可得答案.
3.【答案】 B
【解析】【解答】解:∵y=x2-2ax +1
∴对称轴为x=a
点A、B的情况:n>m,故点B比点A离对称轴远,故y2>y1;
点A、C的情况:m
点B,C的情况:b
∴故y1
【分析】先确定二次函数图象的对称轴,然后运用二次函数的性质进行解答即可.
4.【答案】 A
【解析】【解答】∵ ,
∴ ,有最大值为 ,
∴抛物线开口向下,
∵抛物线 对称轴为直线 ,
设A( , )的对称点为A′( , ),
∴
∴ ,
∵ , ,
∴ ,
∴ .
故答案为:A.
【分析】根据二次函数的性质得到抛物线 的开口向下,有最大值为 ,对称轴为直线 ,设A( , )的对称点为A′( , ),从而求得 ,由 , ,得出 ,则在对称轴右侧,y随x的增大而减小,所以 时, .
5.【答案】 B
【解析】【解答】观察二次函数的图象可知:y1<y3<y2 .
故答案为:B.
【分析】先画出图象,利用图像直接写出结果.
6.【答案】 <
【解析】【解答】当x=﹣2时,y1=(﹣2+3)2=1,当x=2时,y2=(2+3)2=25,y1<y2 , 故答案为<.
【分析】将x=-2,x=2分别代入解析式中,求出y1与,y2的值,然后比较即可.
二、二次函数性质——增减性
7.【答案】 A
【解析】【解答】∵二次函数 的开口向下,
∴所以在对称轴的左侧y随x的增大而增大.
∵二次函数 的对称轴是 ,
∴ .故答案为:A.
【分析】由于抛物线开口向下,在对称轴的左侧y随x的增大而增大,据此即可求出x的范围.
8.【答案】 C
【解析】【解答】解:∵-1<0,
∴y=﹣x2﹣4x+5的对称轴为x= =﹣2,图象开口向下,
∴x≤﹣2时,y随x的增大而增大;故A选项不正确;
∵﹣x2﹣4x+5=0时的两个根为x=﹣5,x=1,
∴当﹣5<x<1时,y>0;故B选项不正确;
∵-2-(﹣4)>﹣ -(﹣2),
∴点A到对称轴的距离大于点B到对称轴的距离,
∴y1<y2;故C选项正确;
当x=﹣2时,y有最大值9,故D选项不正确.
故答案为:C.
【分析】首先求出二次函数的对称轴,然后判断出单调性,据此可判断选项A;求出二次函数所对应的一元二次方程的两根,然后根据单调性可判断选项B;根据二次函数的单调性可判断选项C;由于二次函数开口向下,故在对称轴处取得最大值,据此可判断D.
9.【答案】 m=-2(不唯一,m为不大于-2的整数)
【解析】【解答】解:k > 0,-k<0,抛物线开口向下,
抛物线对称轴 ,
在对称轴的左侧,y随x增大而增大,
∵ ,
∴ ,
∴ ,
∵m为整数 ,
∴m=-2(不唯一).
故m=-2(不唯一,m为不大于-2的整数).
【分析】由二次函数的对称轴可得抛物线对称轴,根据抛物线开口朝下,且 当x < m时,y随着x的增大而增大可得对称轴≤m,由 k > 0 可得m范围,即可找到符合题意的值.
10.【答案】 C
【解析】【解答】∵抛物线y=ax2+bx+c经过(0,3)、(2,3)两点,∴对称轴x 1;
点(﹣1,0)关于对称轴对称点为(3,0),因此它的图象与x轴的另一个交点坐标是(3,0).
故答案为:C.
【分析】根据(0,3)、(2,3)两点求得对称轴,再利用对称性解答即可.
11.【答案】 ④
【解析】【解答】解:由题意可知函数图象过点 、 和 ,
,解得 ,
抛物线解析式为 ,
抛物线开口向上,对称轴为 ,最小值为 ,当 时 随 的增大而增大,
正确的是④,
故答案为:④.
【分析】首先根据表格提供的数据,利用待定系数法求出抛物线的解析式,然后将抛物线的解析式配成顶点式,根据抛物线的系数、图象与性质即可一一判断得出答案。
三、二次函数性质——系数之间的关系
12.【答案】 D
【解析】【解答】∵抛物线开口向下,对称轴大于1,与y轴交于正半轴,∴a<0,﹣ >1,c>0,∴b>﹣2a,∴b+2a>0.
故答案为:D.
【分析】由抛物线开口向下知a<0,由抛物线的对称轴直线大于1,得出b>﹣2a,b>0,即b+2a>0,由抛物线与y轴的交点在y轴的正半轴,得出c>0.
13.【答案】 C
【解析】【解答】抛物线的开口向上,则a>0;
对称轴为x=﹣ =1,即b=﹣2a,故b<0,故(2)错误;
抛物线交y轴于负半轴,则c<0,故(1)正确;
把x=2代入y=ax2+bx+c得:y=4a+2b+c<0,故(3)错误;
把x=1代入y=ax2+bx+c得:y=a+b+c<0,把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c<0,
则(a+b+c)(a﹣b+c)>0,故(4)错误;
不正确的是(2)(3)(4);
故答案为:C.
【分析】根据抛物线的开口方向可判断a的符号,根据抛物线与y轴的交点可得出c值,再根据图象经过的点的情况进行推理,即可对结论进行判断。
14.【答案】 D
【解析】【解答】根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
对称轴:x= >0,
①∵它与x轴的两个交点分别为( 1,0),(3,0),
∴对称轴是x=1,
∴ =1,
∴b+2a=0,
故①正确;
②∵a>0, =1,
∴b<0,
又∵c<0,
∴abc>0,
故②错误;
③∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,
由①知,b= 2a,
∴8a+c>0;
故④正确;
综上所述,正确的结论是:①③④,
故答案为:D.
【分析】根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,对称轴在y轴的右侧,则a,b异号,故b<0,abc>0;由根据抛物线的对称性及与x轴两个交点的坐标得出其对称轴直线是x=1,故b+2a=0;由抛物线与x轴有两个交点,故b2﹣4ac>0;根据图示知,当x=4时,y>0,即16a+4b+c>0,故8a+c>0。
15.【答案】 C
【解析】【解答】①∵抛物线开口向下,
抛物线对称轴位于y轴的左侧,则a、b同号,故ab>0,
抛物线与y轴交于负半轴,则c<0,故abc<0,
故①正确;
②∵抛物线开口方向向下,
∴a<0,
∵x=- =h,且-2<h<-1,
∴4a<b<2a,
∴4a-b<0,
又∵h<0,
∴- <1
∴2a+b<0,
∴(4a-b)(2a+b)>0,
故②错误;
③由②知:b>4a,
∴2b-8a>0①.
当x=-2时,4a-2b+c>0②,
由①+②得:4a-8a+c>0,即4a-c<0.
故③正确;
④∵当x=-1时,a-b+c>0,
∵OC=OB,
∴当x=c时,y=0,即ac2+bc+c=0,
∵c≠0,
∴ac+b+1=0,
∴ac=-b-1,
则(a+1)(c+1)=ac+a+c+1=-b-1+a+c+1=a-b+c>0,
故④正确;
所以本题正确的有:①③④,
故答案为:C.
【分析】由抛物线开口向下,知a<0,抛物线对称轴位于y轴的左侧,则a、b同号,故,b<0,抛物线与y轴交于负半轴,则c<0;由抛物线的对称轴直线-2<h<-1,根据对称轴公式及不等式的性质得出4a<b<2a,进而得出4a-b<0,2a+b<0,故(4a-b)(2a+b)>0;由于b>4a,根据不等式的性质得出2b-8a>0,又当x=-2时,4a-2b+c>0,故4a-8a+c>0,即4a-c<0;当x=-1时,a-b+c>0,又OC=OB,当x=c时,y=0,即ac2+bc+c=0,根据等式的性质得出ac+b+1=0,即ac=-b-1,故(a+1)(c+1)=ac+a+c+1=-b-1+a+c+1=a-b+c>0。
16.【答案】 ①②③
【解析】【解答】∵抛物线的开口向下,
∵与y轴的交点为在y轴的正半轴上,
故①正确;
∵对称轴为x=1抛物线与x轴的一个交点为
∴另一个交点为
∴方程 的根是
故②正确;
当x=1时,
故③正确;
a,b异号,即
当 时,y随x的增大而减小,故④错误.
∴其中正确的说法有①②③;
故答案为:①②③.
【分析】由抛物线的开口向下,知a < 0 ,由抛物线与y轴的交点在y轴的正半轴上,知c > 0 ,故a c < 0 ;对称轴直线及抛物线与x轴的一个交点,由抛物线的对称轴性即可得出抛物线与x轴的另一个交点的坐标,由抛物线与x轴的交点坐标即可得出方程 ax2+bx+c=0 的根;当x=1时, y=a+b+c>0 ,当x>1时,图像从左至右下降,故y随x的增大而减小.
17.【答案】 ①③⑤⑥
【解析】【解答】①如图,抛物线开口方向向下,则a<0.故①正确;
②如图,抛物线对称轴x=- =1,则b=-2a>0.即b>0,故②错误;
③如图,抛物线与y轴交于正半轴,则c>0,故③正确;
④如图,当x=2时,y>0,即4a+2b+c>0,故④错误;
⑤由抛物线对称轴x=- =1得到b+2a=0.故⑤正确;
⑥如图,抛物线与x轴有2个交点,则b2-4ac>0,故⑥正确;
综上所述,正确的结论是①③⑤⑥
【分析】由抛物线开口方向向下,知a<0;由抛物线的对称轴直线是x=1得出b=-2a>0.即b>0,b+2a=0;由抛物线与y轴交于正半轴,知c>0;由图像知:当x=2时,y>0,即4a+2b+c>0;由抛物线与x轴有2个交点,知:b2-4ac>0,综上所述即可得出答案。
18.【答案】 C
【解析】【解答】∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以②正确;
∵x=- =1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,所以③错误;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,故当x1<x2<0时,y1<y2.所以⑤正确.
故答案为①②⑤.
【分析】由抛物线与x轴有2个交点,知b2-4ac>0;由抛物线的对称轴直线及抛物线与x轴一个交点的坐标,即可判断出抛物线与x轴的另一个交点的坐标,根据抛物线与x轴交点的纵坐标即可知道方程ax2+bx+c=0的根的情况;由对称轴直线是x=1得出b=-2a,而x=-1时,y=0,即a-b+c=0,故a+2a+c=0;由于自变量的取值在-1<x<3时,图像位于x轴的上方,故对应的函数值大于0,即y>0;由图像知:当x<1时,图像从左至右上升,此时y随x增大而增大,故当x1<x2<0时,y1<y2。
19.【答案】 ①②④⑤
【解析】【解答】抛物线与y轴交于原点,c=0,故①正确;
该抛物线的对称轴是: ,直线x=﹣1,故②正确;
当x=1时,y=a+b+c
∵对称轴是直线x=﹣1,∴﹣b/2a=﹣1,b=2a.又∵c=0,∴y=3a,故③错误;
x=m对应的函数值为y=am2+bm+c,x=﹣1对应的函数值为y=a﹣b+c.又∵x=﹣1时函数取得最小值,∴a﹣b+c<am2+bm+c,即a﹣b<am2+bm.∵b=2a,∴am2+bm+a>0(m≠﹣1).故④正确.∵|100+1|>|﹣100+1|,且开口向上,∴y1>y2 . 故⑤正确.
故答案为:①②④⑤.
【分析】根据抛物线与y轴的交点判断c和0的关系,再根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断。
四、二次函数性质——最值
20.【答案】 D
【解析】【解答】解:∵在二次函数 中,a=2>0,顶点坐标为(4,6),
∴函数有最小值为6.
故答案为:D.
【分析】该二次函数表达式为顶点式,由于张口向上,即可得出函数有最小值,结合顶点坐标即可解答.
21.【答案】 B
【解析】【解答】解:∵二次函数 ,
∴抛物线的对称轴为:x=1,
∵函数开口向上,
∴当x≥2时,y随x的增大而增大,
∴当x=2时,y最小值=(2-1)2-4=-3
故答案为:B
【分析】根据二次函数y=(x-1)2-4,可以得到当x>1时,该函数有最小值,故可得结论.
22.【答案】 D
【解析】【解答】∵由 知当x=2,最小值为-2,又∵x=-1与x=3关于x=2对称故最大值为 ,
故答案为:D。
【分析】先配方,∵对称轴x=2,在给定定义域范围内,故最小值可求。图像张口向上,故离图像最远的点为最大值。
23.【答案】 C
【解析】【解答】解:∵ ,
∴该抛物线的对称轴是直线x=﹣1,
∵当 时, 随 的增大而减小,
∴a<0,
∵当 时, 的最小值为15,
∴当x=1时,y=15,
即 ,解得: ,
∵a<0,∴a=﹣2.
故答案为:C.
【分析】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向下a<0,再由 时, 的最小值为15,可得当x=1时,y=15,即可求得a。
24.【答案】 D
【解析】【解答】解:∵a+b=3,c﹣3a=-6,
∴b=3﹣a,c=3a-6.
∵b,c都是非负数,
∴ ,
解不等式①得:a≤3,
解不等式②得:a≥ ,
∴2≤a≤3.
又∵a是非负数,
∴2≤a≤3,
S=a2+b+c=a2+(3﹣a)+3a-6=a2+2a-3,
∴对称轴为直线a=﹣ =﹣1,
∴a=2时,最小值n=5,
∴a=3时,最大值m=32+2×3-3=12,
∴m﹣n=12﹣5=7.
故答案为:D.
【分析】用a表示出b、c并求出a的取值范围,再代入S整理成关于a的函数形式,然后根据二次函数的增减性求出m、n的值,再相减即可得解.
25.【答案】 -1;8
【解析】【解答】由二次函数公式可得:对称轴为直线x=3;
x=3在0≤x≤4范围内,故x=3时,函数有最小值-1.
当x=0时,函数取到最大值8.
【分析】根据x=-可求得对称轴方程;结合已知和二次函数的性质可得函数有最小值-1;根据x的范围可知当x=0时,函数取到最大值8.
26.【答案】 1
【解析】【解答】解:∵二次函数y=ax2+2ax+3a2+3(其中x是自变量),
∴对称轴是直线x= = 1,
∵当x≥2时,y随x的增大而增大,
∴a>0,
∵ 2≤x≤1时,y的最大值为9,
∴x=1时,y=a+2a+3a2+3=9,
∴3a2+3a 6=0,
∴a=1,或a= 2(不合题意舍去).
故答案为1.
【分析】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向上a>0,然后由 2≤x≤1时,y的最大值为9,可得x=1时,y=9,即可求出a.
21世纪教育网(www.21cnjy.com)
同课章节目录
