【专题训练】二次函数应用分类练习 (含解析)
文档属性
| 名称 | 【专题训练】二次函数应用分类练习 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 17:17:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数应用分类练习
一、二次函数应用——实际问题
1.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人
A. 56 B. 55 C. 54 D. 53
2.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( )
A. 小球的飞行高度不能达到15m B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s D. 小球飞出1s时的飞行高度为10m
3.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是y=﹣ x2+3.5 B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0) D. 篮球出手时离地面的高度是2m
4.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ 时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.
5.如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.
(1)建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;
(2)求支柱EF的长度;
(3)拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米
6.如图1是一块长为60cm的正方体薄铁片制作的一个长方体盒子,如果要做一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形(如图2),然后把四边折合起来.
(1)求做成的盒子底面积y(cm2)与截去小正方形边长x(cm2)之间的函数关系式;
(2)当做成的盒子的底面积为900cm2时,试求该盒子的容积.
7.足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.
(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
二、二次函数应用——围栏问题
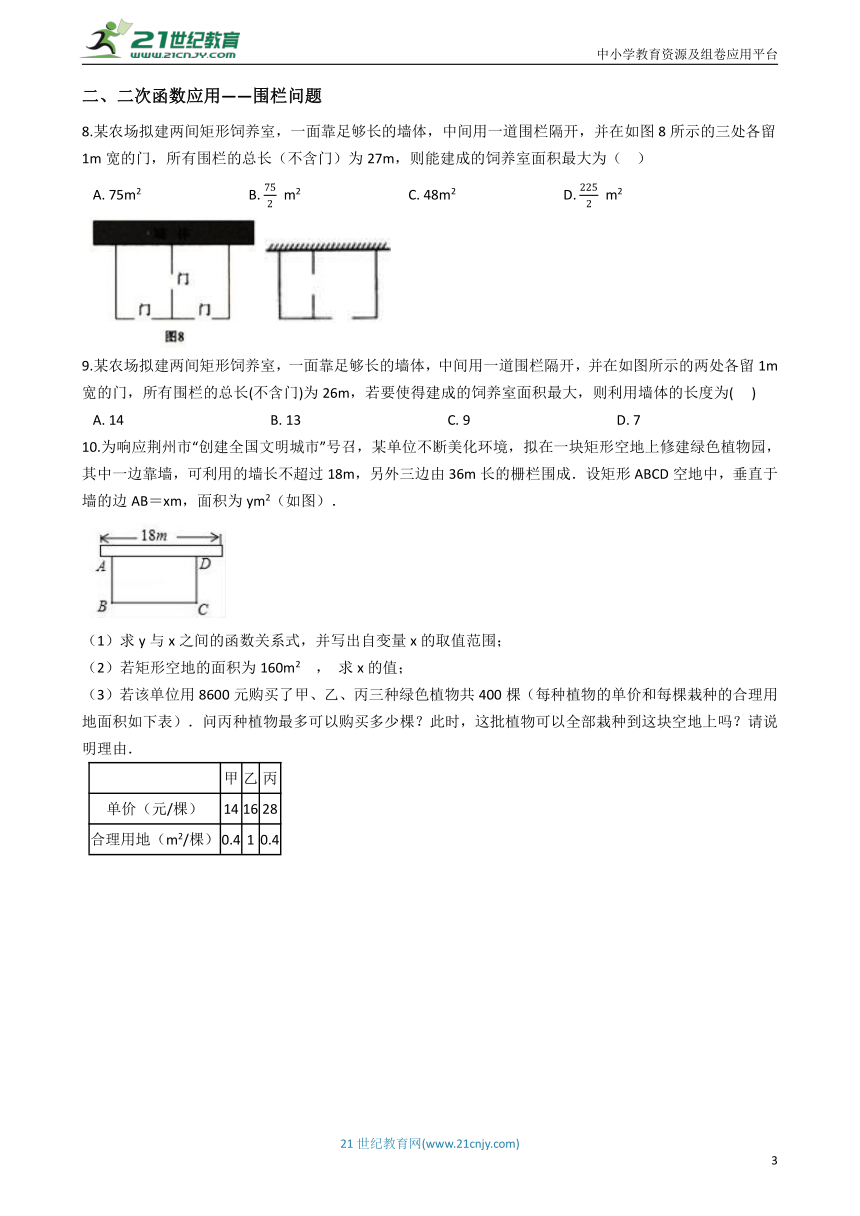
8.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图8所示的三处各留1m宽的门,所有围栏的总长(不含门)为27m,则能建成的饲养室面积最大为( )
A. 75m2 B. m2 C. 48m2 D. m2
9.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m,若要使得建成的饲养室面积最大,则利用墙体的长度为( )
A. 14 B. 13 C. 9 D. 7
10.为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2 , 求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
三、二次函数应用——利润问题
11.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A. B.
C. D.
12.某商店经营皮鞋,所获利润y(元)与销售单价x(元)之间的关系为y=-x2+24x+2956,则获利最多为( ).
A. 3144 B. 3100 C. 144 D. 2956
13.某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
14.旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金是x(元).发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.当每辆车的日租金为多少元时,每天的净收入最多?(注:净收入=租车收入管理费)
15.仙游度尾文旦柚,是莆田四大名果之一,获得“国家地理标志保护产品”。近年来,在政府的指导下,该地果农大力种植文旦柚,取得了较好的经济收入。某果园有130棵柚子树,每棵树结150个柚子,现准备多种一些柚子树以提高果园产量,但如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少,根据经验估计,每多种一棵树,平均每棵树就会少结1个柚子。假设果园多种了x棵柚子树.
(1)直接写出平均每棵树结的柚子个数n(个)与x之间的关系;
(2)果园多种多少棵柚子树时,可使柚子的总产量y最大?最大值为多少?
16.某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
(1)求y关于 的函数关系式,并写出自变量 的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
17.某快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本). 若每份套餐售价不超过10元,每天可销售400份;若每份套餐售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店每天的利润.
(1)若每份套餐售价不超过10元.
①试写出y与x的函数关系式;
②若要使该店每天的利润不少于800元,则每份套餐的售价应不低于多少元?
该店把每份套餐的售价提高到10元以上,每天的利润能否达到1560元?若能,求出每份套餐的售价应定为多少元时,既能保证利润又能吸引顾客?若不能,请说明理由.
四、二次函数应用——函数之间关系
18.如图,抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1), 则关于x的方程ax2=bx+c的解为________.
19.如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )
A. h> B. 0<h≤ C. h>2 D. 0<h<2
20.已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1, 0)、(2,0),抛物线与直线交点的横坐标为1和 ,那么不等式mx+n <ax2+bx+c <0的解集是( )
A. 1< x <2 B. x < 或 x >1 C. < x <2 D. -1< x <2
21.如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≤(x-2)2+m的x的取值范围.
22.已知抛物线 (a、b、c是常数, )的对称轴为直线 .
(1)b=________;(用含a的代数式表示)
(2)当 时,若关于x的方程 在 的范围内有解,求c的取值范围;
(3)若抛物线过点( , ),当 时,抛物线上的点到x轴距离的最大值为4,求a的值.
23.根据下列要求,解答相关问题.
(1)请补全以下求不等式 的解集的过程:
① 构造函数,画出图象:根据不等式特征构造二次函数y= ;并在下面的坐标系中(图1)画出二次函数y= 的图象________(只画出大致图象即可);
② 求得界点,标示所需:当 时,求得方程 的解为________;并用虚线标示出函数y= 图象中 <0的部分;
③借助图象,写出解集:由所标示图象,可得不等式 <0的解集为________.
(2)请你利用上面求不等式解集的过程,求不等式 -3≥0的解集.
答案解析部分
一、二次函数应用——实际问题
1.【答案】 B
【解析】【解答】解:设旅行团人数为x人,此时的营业额为y元,则 ,
由题意得: ,
由二次函数的性质可知,在 内,当 时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
【分析】设旅行团人数为x人,此时的营业额为y元,由题意可列出利润与x的函数关系式,进而求得最值得出答案。
2.【答案】 C
【解析】【解答】A、当h=15时,15=20t﹣5t2 ,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项不符合题意;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项不符合题意;
C、∵h=0时,0=20t﹣5t2 ,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项符合题意;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项不符合题意;
故答案为:C.
【分析】直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
3.【答案】 A
【解析】【解答】解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得 3.05=a×1.52+3.5,
∴a=﹣ ,
∴y=﹣ x2+3.5.
符合题意;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
不符合题意;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
不符合题意;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
y=﹣0.2×(﹣2.5)2+3.5=2.25m.
∴这次跳投时,球出手处离地面2.25m.
不符合题意.
故答案为:A.
【分析】先根据函数图像,利用待定系数法求出函数的解析式,可对选项A作出判断;再求出y=3.05时,x的值,就可得出篮圈中心的坐标,可对选项B作出判断;观察图像可直接得出顶点坐标,可对选项C作出判断;根据当球运动的水平距离为2.5m时,达到最大高度3.5m,求出x=-2.5时y的值,可对选项D作出判断,继而可得出答案。
4.【答案】 (1)解:①当a= 时, ,将点P(0,1)代入,得: ×16+h=1,解得:h= ;
②把x=5代入 ,得: =1.625,∵1.625>1.55,∴此球能过网
(2)解:把(0,1)、(7, )代入 ,得: ,解得: ,∴a=
【解析】【分析】(1)由题意分别把a=-和点P(0,1)、x=5代入解析式计算即可求解;
(2)由题意知抛物线过点(0,1)和点(7,),所以用待定系数法计算即可求解析式。
5.【答案】 (1)解:根据题意,设拱桥抛物线的函数表达式为: ,
∵相邻两支柱间的距离均为5m,
∴OA=4×5m=20m,
∴(20,0),(10,6)两点都在抛物线上,
∴ ,解得
∴ .
(2)解:设点F的坐标为(15,y),
∴ .
∴EF=8m m= m=3.5m.
(3)解:当y=3+0.3=3.3(m)时,有 ,
化简,得 ,
解得 , , ,
∴ .
答:行车道最宽可以铺设13.4米.
【解析】【分析】(1)根据所建的直角坐标系表示出抛物线上的点的坐标,用待定系数法求得抛物线解析式;
(2)将F的横坐标代入抛物线解析式,即可求得点F的纵坐标,然后求EF的长度。
(3)把y=3+0.3=3.3代入抛物线的解析式,求得对应的x的值,则两个横坐标之间的距离即为行车道的最宽距离。
6.【答案】 (1)解:由题意可得y=(60﹣2x)2=4x2﹣240x+3600(0<x<30);
(2)解:当y=900时,(60﹣2x)2=900,解得x=15,x=45(不合题意舍去).
因此盒子的容积应该是900×15=13500(立方厘米).
答:该盒子的容积是13500立方厘米.
【解析】【分析】(1)由题意知盒子底面是一个边长为(60-2x)cm的正方形,根据正方形面积公式计算即得;
(2)依据题意,可列方程(60﹣2x)2=900,解出符合题意的x值即可得到剪掉的小正方形的边长,再根据正方体的体积公式即可求出盒子的容积。
7.【答案】 (1)解:设y关于x的函数关系式为y=ax2+bx.依题可知:
当x=1时,y=2.44;
当x=3时,y=0.∴ ,∴ ,
∴y=-1.22x2+3.66x.
(2)解:不能.
理由:∵y=4.88,
∴4.88=-1.22x2+3.66x,
∴x2-3x+4=0.
∵(-3)2-4×4<0,
∴方程4.88=-1.22x2+3.66x无解.
∴足球的飞行高度不能达到4.88m.
(3)解:∵y=2.44,∴2.44=-1.22x2+3.66x,∴x2-3x+2=0,
∴x1=1(不合题意,舍去),x2=2.
∴离球门左边框12m处的守门员至少要在2s内到球门的左边框.
【解析】【分析】(1)根据题意,结合图像,可得出抛物线经过点(0,0)(1,2.44),(3,0),再利用待定系数法求出抛物线的解析式。
(2)利用(1)中的函数解析式,将y=4.88代入函数解析式,可得出方程无解,即可得出答案。
(3)利用(1)中的函数解析式,将y=2.44代入函数解析式,求出x的值,再得出符合题意的x的值。
二、二次函数应用——围栏问题
8.【答案】 A
【解析】【解答】解:设垂直于墙的材料长为x米,则平行于墙的材料为27+3-3x=30-3x米,饲养室的面积为Sm2,
∴S=(30-3x)x=-3x2+30x=-3(x-5)2+75,
∴ 饲养室面积最大75平方米.
故答案为:A.
【分析】设垂直于墙的材料长为x米,则平行于墙的材料为27+3-3x=30-3x米,饲养室的面积为Sm2,利用矩形的面积公式可得S=-3x2+30x,将其化为顶点式,从而求出最大值.
9.【答案】 A
【解析】【解答】解:设建成的饲养室面积为Sm2 , 垂直于墙的一边长为xm,则平行于墙的一边长为26+2-3x=(28-3x)m.
S=x(28-3x)=-3x2+28x,
对称轴为直线 ,
∴a=-3,抛物线的开口向下,当时,S有最大值,
∴
∵一面靠足够长的墙体,
∴利用墙体的长度为14m.
故答案为:A
【分析】由题意可知设建成的饲养室面积为Sm2 , 垂直于墙的一边长为xm,则平行于墙的一边长为(28-3x)m,利用矩形的面积公式建立S与x的函数解析式,再利用二次函数的性质求出x的值及28-3x的值,然后根据一面靠足够长的墙体可得答案。
10.【答案】 (1)解:y=x(36﹣2x)=﹣2x2+36x(9≤x<18)
(2)解:由题意:﹣2x2+36x=160,
解得x=10或8.
∵x=8时,36﹣16=20>18,不符合题意,
∴x的值为10.
(3)解:∵y=﹣2x2+36x=﹣2(x﹣9)2+162,
∴x=9时,y有最大值162,
设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,
由题意:14(400﹣a﹣b)+16a+28b=8600,
∴a+7b=1500,
∴b的最大值为214,此时a=2,
需要种植的面积=0.4×(400﹣214﹣2)+1×2+0.4×214=161.2<162,
∴这批植物可以全部栽种到这块空地上.
【解析】【分析】(1)先用含x的代数式表示出BC的长为(36-2x),然后根据矩形的面积公式计算即可。最后根据各边长大于0和BC的长不超过墙长列出不等式组,解之求出x的取值范围。
(2)当y=160时得 -2x2+36x=160, 解方程求得x的值,注意检验x的值是否符合题意(在取值范围内)。
(3)先根据二次函数的性质求出面积的最大值;又设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,根据购买总费列出方程,从而求得b的最大整数值为214,此时a=2,然后求出此时的种植面积,由此时的种植面积小于空地的最大面积判断出这批植物可以全部栽种到这块空地上.
三、二次函数应用——利润问题
11.【答案】 C
【解析】【解答】设销售单价为每千克x元,此时的销售数量为 ,每千克赚的钱为
则 .
故答案为:C.
【分析】根据月销售利润为y=(每千克的售价-每千克的成本价)×此时的销售数量,列出函数解析式,可解答。
12.【答案】 B
【解析】【解答】∵ y=-x2+24x+2956 ∴y=-(x-12)2 +3100,当x=12时 y最大为3100元.
【分析】本题考查二次函数的应用和最值问题.
13.【答案】 C
【解析】【解答】设每张床位提高x个20元,每天收入为y元.
则有y=(100+20x)(100-10x)
=-200x2+1000x+10000.
当x=- 时,可使y有最大值.
又x为整数,则x=2时,y=11200;
x=3时,y=11200;
则为使租出的床位少且租金高,每张床收费=100+3×20=160元.
故答案为:C.
【分析】设每张床位提高x个20元,每天收入为y元。根据等量关系:每天的收入y=每张床的费用×每天出租的床位,列出y与x的函数解析式,再利用公式求出答案。注意x为整数。
14.【答案】 解:设每天的净收入为y元,当0<x≤100时,y1=50x-1100,∵y1随x的增大而增大,∴当x=100时,y1的最大值为50×100-1100=3900;当x>100时,y2=(50- )x-1100=- x2+70x-1100=- (x-175)2+5025,当x=175时,y2的最大值为5025,5025>3900,故当每辆车的日租金为175元时,每天的净收入最多是5025元.
【解析】【分析】先分别求出当0<x≤100时和当x>100时,y与x的函数解析式,再在每一段内求出函数的最大值,然后比较大小得出函数的最大值。
15.【答案】 (1)解:平均每棵树结的柚子个数n(个)与x之间的关系为:
n=150-x(0≤x<150).
(2)解:设果园多种x棵柚子树时,可使柚子的总产量为y,则
y=(150-x)(130+x)=-x2+20x+19500=-(x-10)2+19600,
∴当x=10时,y最大=19600.
即当果园多种10棵柚子树时,可使柚子的总产量最大,最大为19600个.
【解析】【分析】(1)根据题意,直接写出n与x的关系式。
(2)利用柚子的总产量y=平均每棵树结的柚子个数n×树的总数量,列出y与x的函数解析式,再将函数解析式转化为顶点式,利用二次函数的性质,可解答。
16.【答案】 (1)解:由图可设玩具批发价m,数量为n,则m=kn+b( ),
把 (50,80),(100,60)代入可求得 .
由题意得 ,解得 .
①当 时, ;
②当 时,
(2)解:∵甲商店数量不超过100个,∴ ,∴ .
∵ , .
∴x=70时,y最大值=9040(元).
两商店联合购买需120×60=7200(元),
∴最多可节约9040-7200=1840(元)
(3)解:单独购买不变,联合购买需120(60- a)=7200-120a(元),
∴9040-(7200-120a)=2800,解得a=8.
【解析】【分析】(1)根据题意,乙商店所需数量不超过50个,所以120-x≤50,求出x的物质范围,根据图象求出单价与数量的关系,注意这里是分段函数,付款综合y=甲商店的费用+乙商店费用=甲的单价×甲的数量+乙的单价×乙的数量。
(2)找出y关于x的函数关系式,在70≤x≤100,y的最大值,再减去甲、乙两商店联合购买的费用60×120就可得。
(3)根据题意可列一元一次方程9040=120×(60-a)=2800,可解得a的只。
17.【答案】 (1)解:①y=400(x﹣5)﹣600.(5<x≤10),
②依题意得:400(x﹣5)﹣600≥800, 解得:x≥8.5,
∵5<x≤10,且每份套餐的售价x(元)取整数, ∴每份套餐的售价应不低于9元.
(2)解:依题意可知:每份套餐售价提高到10元以上时,y=(x﹣5)[400﹣40(x﹣10)]﹣600,当y=1560时, (x﹣5)[400﹣40(x﹣10)]﹣600=1560,解得:x1=11,x2=14,为了保证净收入又能吸引顾客,应取x1=11,即x2=14不符合题意.
故该套餐售价应定为11元.
【解析】【分析】(1)①每天的利润y=每一份套餐的利润×销售量-每天固定支出费用,列出y与x的函数解析式,写出自变量的取值范围即可;②每一份套餐的利润×销售量-每天固定支出费用≥800,列不等式求解,得出符合条件的x的值。
(2)根据每天的利润能=1560,建立方程求出x的值,再根据为了保证净收入又能吸引顾客,确定符合题意的x的值。
四、二次函数应用——函数之间关系
18.【答案】
【解析】【解答】解:∵ 抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),
∴ 关于x的方程ax2=bx+c的解 为: ;
故答案为: 。
【分析】求关于x的方程ax2=bx+c的解 就是抛物线y=ax2和直线y=bx+c的两个交点的横坐标。
19.【答案】 C
【解析】【解答】解:对于抛物线 ,
当 时, ,解得 或 ,
则 ,
的面积为3,
,即 ,解得 ,
,
将点 代入抛物线解析式得: ,解得 ,
则抛物线的解析式为 ,
将抛物线向左平移 个单位所得抛物线为 ,
当 时, 随 的增大而增大,
设直线 的函数解析式 ,
将点 代入得: ,解得 ,
则直线 的函数解析式 ,
当直线 与 没有公共点时,则只需 时,直线 的函数值大于抛物线 的函数值,
即 ,
解得 ,
故答案为:C.
【分析】先根据抛物线的解析式可得点 A,B 的坐标,从而可得 AB 长,再利用三角形的面积公式可得 OC 的长,从而可得点 C 的坐标,利用待定系数法可求出抛物线的解析式和一次函数的解析式,然后根据二次函数图象的平移规律、增减性求解即可得.
20.【答案】 A
【解析】【解答】解:∵ 抛物线与x轴交于点(-1, 0), 抛物线与直线交点的横坐标为1和
∴ 不等式mx+n <ax2+bx+c <0的解集为:1<x<2
【分析】根据已知条件: 抛物线与x轴交于点(-1, 0), 抛物线与直线交点的横坐标为1和 , 观察函数图像可得出不等式mx+n <ax2+bx+c <0的解集。
21.【答案】 (1)解:将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1,所以二次函数解析式为y=(x-2)2-1;当x=0时,y=4-1=3,所以C点坐标为(0,3),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,
所以B点坐标为(4,3),将A(1,0)、B(4,3)代入y=kx+b得 ,解得 ,
所以一次函数解析式为y=x-1;
(2)解:观察图象可得x的取值范围:x≤1或x≥4.
【解析】【分析】(1)将点A代入二次函数解析式,求出m的值,可得出二次函数解析式,求出点C的坐标,再根据C和B关于对称轴对称,可得出点B的坐标,然后利用待定系数法求出一次函数解析式。
(2)观察直线x=1和直线x=4时,写出一次函数的图像低于二次函数的图像时的x的取值范围。
22.【答案】 (1)4a
(2)解:当a = -1时,∵关于x的方程 在-3< x <1的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,∴b2 -4ac =16+4c ≥0,即c ≥ -4.
∴抛物线y= x2 +4x=(x+2)2 -4与直线y = c在-3当x= -2时,y= -4,当x=1时,y= 5.
故可得: -4≤ c< 5.
(3)解:∵抛物线y=ax2+4ax+c过点(-2,-2),∴c = 4a -2.∴抛物线解析式为: .
① 当a > 0时,抛物线开口向上.
∵抛物线对称轴为x=-2.
∴当-1≤x≤0时,y随x增大而增大.
∵抛物线上的点到x轴距离的最大值为4,
由图像可知:4a -2=4.
∴ .
② 当a < 0时,抛物线开口向下.
∵抛物线对称轴为x=-2.∴当-1≤x≤0时,y随x增大而减小.∵抛物线上的点到x轴距离的最大值为4,由图像可知:4a -2= -4.∴ . 综上所述: .
【解析】【解答】解:(1)∵抛物线 (a、b、c是常数, )的对称轴为直线 ,
∴ ,
∴b=4a ;
【分析】(1)根据抛物线的对称轴公式即可得出,故b=4a ;
(2)当a= 1 时,若关于x的方程 ax2+bx+c=0 在 3 < x < 1 的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,从函数图像的观点看,则抛物线y= x2 +4x=(x+2)2 -4与直线y = -c在-3(3)将抛物线的顶点坐标代入抛物线的顶点式得出抛物线解析式为:y=ax2+4ax+4a 2=a(x+2)2 2 . ① 当a > 0时,抛物线开口向上.又抛物线对称轴为x=-2.故当-1≤x≤0时,y随x增大而增大.又抛物线上的点到x轴距离的最大值为4,由图形得4a -2=4. 求解得出a的值;② 当a < 0时,抛物线开口向下.由抛物线对称轴为x=-2.故当-1≤x≤0时,y随x增大而减小.又抛物线上的点到x轴距离的最大值为4,由图像可知:4a -2= -4求解得出a的值,综上所述即可得出答案。
23.【答案】 (1)解: ;;
(2)解:函数y=x2-2x-3的图象如图2所示,
∵A(-1,0),B(3,0),
∴不等式x2-2x-3≥0的解集,由图象可知,x≥3或x≤-1
【解析】【解答】(1)二次函数y=x2-2x的图象如图1所示,
∵二次函数y=x2-2x与x轴交于O(0,0),A(2,0),
∴方程x2-2x=0的解为x=0或2.
由图象可知x2-2x<0的解集为0<x<2.
故答案为x=0或2,0<x<2.
【分析】(1)① 画出二次函数y= x2 2x的图像即可;②求出当y=0时的自变量x的值,用虚线画出x轴下方的抛物线;③观察x轴下方的函数图像,利用抛物线与x轴的两交点坐标,可得出不等式 x2 2x <0的解集。
(2)画出抛物线y=x2 2x -3的大致图像,再求出此抛物线与x轴的交点A、B的坐标,再观察x轴上方的函数图像,可得出答案。
21世纪教育网(www.21cnjy.com)
二次函数应用分类练习
一、二次函数应用——实际问题
1.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人
A. 56 B. 55 C. 54 D. 53
2.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( )
A. 小球的飞行高度不能达到15m B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s D. 小球飞出1s时的飞行高度为10m
3.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是y=﹣ x2+3.5 B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0) D. 篮球出手时离地面的高度是2m
4.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ 时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.
5.如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.
(1)建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;
(2)求支柱EF的长度;
(3)拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米
6.如图1是一块长为60cm的正方体薄铁片制作的一个长方体盒子,如果要做一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形(如图2),然后把四边折合起来.
(1)求做成的盒子底面积y(cm2)与截去小正方形边长x(cm2)之间的函数关系式;
(2)当做成的盒子的底面积为900cm2时,试求该盒子的容积.
7.足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.
(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
二、二次函数应用——围栏问题
8.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图8所示的三处各留1m宽的门,所有围栏的总长(不含门)为27m,则能建成的饲养室面积最大为( )
A. 75m2 B. m2 C. 48m2 D. m2
9.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m,若要使得建成的饲养室面积最大,则利用墙体的长度为( )
A. 14 B. 13 C. 9 D. 7
10.为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2 , 求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
三、二次函数应用——利润问题
11.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A. B.
C. D.
12.某商店经营皮鞋,所获利润y(元)与销售单价x(元)之间的关系为y=-x2+24x+2956,则获利最多为( ).
A. 3144 B. 3100 C. 144 D. 2956
13.某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
14.旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金是x(元).发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.当每辆车的日租金为多少元时,每天的净收入最多?(注:净收入=租车收入管理费)
15.仙游度尾文旦柚,是莆田四大名果之一,获得“国家地理标志保护产品”。近年来,在政府的指导下,该地果农大力种植文旦柚,取得了较好的经济收入。某果园有130棵柚子树,每棵树结150个柚子,现准备多种一些柚子树以提高果园产量,但如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少,根据经验估计,每多种一棵树,平均每棵树就会少结1个柚子。假设果园多种了x棵柚子树.
(1)直接写出平均每棵树结的柚子个数n(个)与x之间的关系;
(2)果园多种多少棵柚子树时,可使柚子的总产量y最大?最大值为多少?
16.某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
(1)求y关于 的函数关系式,并写出自变量 的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
17.某快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本). 若每份套餐售价不超过10元,每天可销售400份;若每份套餐售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店每天的利润.
(1)若每份套餐售价不超过10元.
①试写出y与x的函数关系式;
②若要使该店每天的利润不少于800元,则每份套餐的售价应不低于多少元?
该店把每份套餐的售价提高到10元以上,每天的利润能否达到1560元?若能,求出每份套餐的售价应定为多少元时,既能保证利润又能吸引顾客?若不能,请说明理由.
四、二次函数应用——函数之间关系
18.如图,抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1), 则关于x的方程ax2=bx+c的解为________.
19.如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )
A. h> B. 0<h≤ C. h>2 D. 0<h<2
20.已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1, 0)、(2,0),抛物线与直线交点的横坐标为1和 ,那么不等式mx+n <ax2+bx+c <0的解集是( )
A. 1< x <2 B. x < 或 x >1 C. < x <2 D. -1< x <2
21.如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≤(x-2)2+m的x的取值范围.
22.已知抛物线 (a、b、c是常数, )的对称轴为直线 .
(1)b=________;(用含a的代数式表示)
(2)当 时,若关于x的方程 在 的范围内有解,求c的取值范围;
(3)若抛物线过点( , ),当 时,抛物线上的点到x轴距离的最大值为4,求a的值.
23.根据下列要求,解答相关问题.
(1)请补全以下求不等式 的解集的过程:
① 构造函数,画出图象:根据不等式特征构造二次函数y= ;并在下面的坐标系中(图1)画出二次函数y= 的图象________(只画出大致图象即可);
② 求得界点,标示所需:当 时,求得方程 的解为________;并用虚线标示出函数y= 图象中 <0的部分;
③借助图象,写出解集:由所标示图象,可得不等式 <0的解集为________.
(2)请你利用上面求不等式解集的过程,求不等式 -3≥0的解集.
答案解析部分
一、二次函数应用——实际问题
1.【答案】 B
【解析】【解答】解:设旅行团人数为x人,此时的营业额为y元,则 ,
由题意得: ,
由二次函数的性质可知,在 内,当 时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
【分析】设旅行团人数为x人,此时的营业额为y元,由题意可列出利润与x的函数关系式,进而求得最值得出答案。
2.【答案】 C
【解析】【解答】A、当h=15时,15=20t﹣5t2 ,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项不符合题意;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项不符合题意;
C、∵h=0时,0=20t﹣5t2 ,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项符合题意;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项不符合题意;
故答案为:C.
【分析】直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
3.【答案】 A
【解析】【解答】解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得 3.05=a×1.52+3.5,
∴a=﹣ ,
∴y=﹣ x2+3.5.
符合题意;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
不符合题意;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
不符合题意;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
y=﹣0.2×(﹣2.5)2+3.5=2.25m.
∴这次跳投时,球出手处离地面2.25m.
不符合题意.
故答案为:A.
【分析】先根据函数图像,利用待定系数法求出函数的解析式,可对选项A作出判断;再求出y=3.05时,x的值,就可得出篮圈中心的坐标,可对选项B作出判断;观察图像可直接得出顶点坐标,可对选项C作出判断;根据当球运动的水平距离为2.5m时,达到最大高度3.5m,求出x=-2.5时y的值,可对选项D作出判断,继而可得出答案。
4.【答案】 (1)解:①当a= 时, ,将点P(0,1)代入,得: ×16+h=1,解得:h= ;
②把x=5代入 ,得: =1.625,∵1.625>1.55,∴此球能过网
(2)解:把(0,1)、(7, )代入 ,得: ,解得: ,∴a=
【解析】【分析】(1)由题意分别把a=-和点P(0,1)、x=5代入解析式计算即可求解;
(2)由题意知抛物线过点(0,1)和点(7,),所以用待定系数法计算即可求解析式。
5.【答案】 (1)解:根据题意,设拱桥抛物线的函数表达式为: ,
∵相邻两支柱间的距离均为5m,
∴OA=4×5m=20m,
∴(20,0),(10,6)两点都在抛物线上,
∴ ,解得
∴ .
(2)解:设点F的坐标为(15,y),
∴ .
∴EF=8m m= m=3.5m.
(3)解:当y=3+0.3=3.3(m)时,有 ,
化简,得 ,
解得 , , ,
∴ .
答:行车道最宽可以铺设13.4米.
【解析】【分析】(1)根据所建的直角坐标系表示出抛物线上的点的坐标,用待定系数法求得抛物线解析式;
(2)将F的横坐标代入抛物线解析式,即可求得点F的纵坐标,然后求EF的长度。
(3)把y=3+0.3=3.3代入抛物线的解析式,求得对应的x的值,则两个横坐标之间的距离即为行车道的最宽距离。
6.【答案】 (1)解:由题意可得y=(60﹣2x)2=4x2﹣240x+3600(0<x<30);
(2)解:当y=900时,(60﹣2x)2=900,解得x=15,x=45(不合题意舍去).
因此盒子的容积应该是900×15=13500(立方厘米).
答:该盒子的容积是13500立方厘米.
【解析】【分析】(1)由题意知盒子底面是一个边长为(60-2x)cm的正方形,根据正方形面积公式计算即得;
(2)依据题意,可列方程(60﹣2x)2=900,解出符合题意的x值即可得到剪掉的小正方形的边长,再根据正方体的体积公式即可求出盒子的容积。
7.【答案】 (1)解:设y关于x的函数关系式为y=ax2+bx.依题可知:
当x=1时,y=2.44;
当x=3时,y=0.∴ ,∴ ,
∴y=-1.22x2+3.66x.
(2)解:不能.
理由:∵y=4.88,
∴4.88=-1.22x2+3.66x,
∴x2-3x+4=0.
∵(-3)2-4×4<0,
∴方程4.88=-1.22x2+3.66x无解.
∴足球的飞行高度不能达到4.88m.
(3)解:∵y=2.44,∴2.44=-1.22x2+3.66x,∴x2-3x+2=0,
∴x1=1(不合题意,舍去),x2=2.
∴离球门左边框12m处的守门员至少要在2s内到球门的左边框.
【解析】【分析】(1)根据题意,结合图像,可得出抛物线经过点(0,0)(1,2.44),(3,0),再利用待定系数法求出抛物线的解析式。
(2)利用(1)中的函数解析式,将y=4.88代入函数解析式,可得出方程无解,即可得出答案。
(3)利用(1)中的函数解析式,将y=2.44代入函数解析式,求出x的值,再得出符合题意的x的值。
二、二次函数应用——围栏问题
8.【答案】 A
【解析】【解答】解:设垂直于墙的材料长为x米,则平行于墙的材料为27+3-3x=30-3x米,饲养室的面积为Sm2,
∴S=(30-3x)x=-3x2+30x=-3(x-5)2+75,
∴ 饲养室面积最大75平方米.
故答案为:A.
【分析】设垂直于墙的材料长为x米,则平行于墙的材料为27+3-3x=30-3x米,饲养室的面积为Sm2,利用矩形的面积公式可得S=-3x2+30x,将其化为顶点式,从而求出最大值.
9.【答案】 A
【解析】【解答】解:设建成的饲养室面积为Sm2 , 垂直于墙的一边长为xm,则平行于墙的一边长为26+2-3x=(28-3x)m.
S=x(28-3x)=-3x2+28x,
对称轴为直线 ,
∴a=-3,抛物线的开口向下,当时,S有最大值,
∴
∵一面靠足够长的墙体,
∴利用墙体的长度为14m.
故答案为:A
【分析】由题意可知设建成的饲养室面积为Sm2 , 垂直于墙的一边长为xm,则平行于墙的一边长为(28-3x)m,利用矩形的面积公式建立S与x的函数解析式,再利用二次函数的性质求出x的值及28-3x的值,然后根据一面靠足够长的墙体可得答案。
10.【答案】 (1)解:y=x(36﹣2x)=﹣2x2+36x(9≤x<18)
(2)解:由题意:﹣2x2+36x=160,
解得x=10或8.
∵x=8时,36﹣16=20>18,不符合题意,
∴x的值为10.
(3)解:∵y=﹣2x2+36x=﹣2(x﹣9)2+162,
∴x=9时,y有最大值162,
设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,
由题意:14(400﹣a﹣b)+16a+28b=8600,
∴a+7b=1500,
∴b的最大值为214,此时a=2,
需要种植的面积=0.4×(400﹣214﹣2)+1×2+0.4×214=161.2<162,
∴这批植物可以全部栽种到这块空地上.
【解析】【分析】(1)先用含x的代数式表示出BC的长为(36-2x),然后根据矩形的面积公式计算即可。最后根据各边长大于0和BC的长不超过墙长列出不等式组,解之求出x的取值范围。
(2)当y=160时得 -2x2+36x=160, 解方程求得x的值,注意检验x的值是否符合题意(在取值范围内)。
(3)先根据二次函数的性质求出面积的最大值;又设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,根据购买总费列出方程,从而求得b的最大整数值为214,此时a=2,然后求出此时的种植面积,由此时的种植面积小于空地的最大面积判断出这批植物可以全部栽种到这块空地上.
三、二次函数应用——利润问题
11.【答案】 C
【解析】【解答】设销售单价为每千克x元,此时的销售数量为 ,每千克赚的钱为
则 .
故答案为:C.
【分析】根据月销售利润为y=(每千克的售价-每千克的成本价)×此时的销售数量,列出函数解析式,可解答。
12.【答案】 B
【解析】【解答】∵ y=-x2+24x+2956 ∴y=-(x-12)2 +3100,当x=12时 y最大为3100元.
【分析】本题考查二次函数的应用和最值问题.
13.【答案】 C
【解析】【解答】设每张床位提高x个20元,每天收入为y元.
则有y=(100+20x)(100-10x)
=-200x2+1000x+10000.
当x=- 时,可使y有最大值.
又x为整数,则x=2时,y=11200;
x=3时,y=11200;
则为使租出的床位少且租金高,每张床收费=100+3×20=160元.
故答案为:C.
【分析】设每张床位提高x个20元,每天收入为y元。根据等量关系:每天的收入y=每张床的费用×每天出租的床位,列出y与x的函数解析式,再利用公式求出答案。注意x为整数。
14.【答案】 解:设每天的净收入为y元,当0<x≤100时,y1=50x-1100,∵y1随x的增大而增大,∴当x=100时,y1的最大值为50×100-1100=3900;当x>100时,y2=(50- )x-1100=- x2+70x-1100=- (x-175)2+5025,当x=175时,y2的最大值为5025,5025>3900,故当每辆车的日租金为175元时,每天的净收入最多是5025元.
【解析】【分析】先分别求出当0<x≤100时和当x>100时,y与x的函数解析式,再在每一段内求出函数的最大值,然后比较大小得出函数的最大值。
15.【答案】 (1)解:平均每棵树结的柚子个数n(个)与x之间的关系为:
n=150-x(0≤x<150).
(2)解:设果园多种x棵柚子树时,可使柚子的总产量为y,则
y=(150-x)(130+x)=-x2+20x+19500=-(x-10)2+19600,
∴当x=10时,y最大=19600.
即当果园多种10棵柚子树时,可使柚子的总产量最大,最大为19600个.
【解析】【分析】(1)根据题意,直接写出n与x的关系式。
(2)利用柚子的总产量y=平均每棵树结的柚子个数n×树的总数量,列出y与x的函数解析式,再将函数解析式转化为顶点式,利用二次函数的性质,可解答。
16.【答案】 (1)解:由图可设玩具批发价m,数量为n,则m=kn+b( ),
把 (50,80),(100,60)代入可求得 .
由题意得 ,解得 .
①当 时, ;
②当 时,
(2)解:∵甲商店数量不超过100个,∴ ,∴ .
∵ , .
∴x=70时,y最大值=9040(元).
两商店联合购买需120×60=7200(元),
∴最多可节约9040-7200=1840(元)
(3)解:单独购买不变,联合购买需120(60- a)=7200-120a(元),
∴9040-(7200-120a)=2800,解得a=8.
【解析】【分析】(1)根据题意,乙商店所需数量不超过50个,所以120-x≤50,求出x的物质范围,根据图象求出单价与数量的关系,注意这里是分段函数,付款综合y=甲商店的费用+乙商店费用=甲的单价×甲的数量+乙的单价×乙的数量。
(2)找出y关于x的函数关系式,在70≤x≤100,y的最大值,再减去甲、乙两商店联合购买的费用60×120就可得。
(3)根据题意可列一元一次方程9040=120×(60-a)=2800,可解得a的只。
17.【答案】 (1)解:①y=400(x﹣5)﹣600.(5<x≤10),
②依题意得:400(x﹣5)﹣600≥800, 解得:x≥8.5,
∵5<x≤10,且每份套餐的售价x(元)取整数, ∴每份套餐的售价应不低于9元.
(2)解:依题意可知:每份套餐售价提高到10元以上时,y=(x﹣5)[400﹣40(x﹣10)]﹣600,当y=1560时, (x﹣5)[400﹣40(x﹣10)]﹣600=1560,解得:x1=11,x2=14,为了保证净收入又能吸引顾客,应取x1=11,即x2=14不符合题意.
故该套餐售价应定为11元.
【解析】【分析】(1)①每天的利润y=每一份套餐的利润×销售量-每天固定支出费用,列出y与x的函数解析式,写出自变量的取值范围即可;②每一份套餐的利润×销售量-每天固定支出费用≥800,列不等式求解,得出符合条件的x的值。
(2)根据每天的利润能=1560,建立方程求出x的值,再根据为了保证净收入又能吸引顾客,确定符合题意的x的值。
四、二次函数应用——函数之间关系
18.【答案】
【解析】【解答】解:∵ 抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),
∴ 关于x的方程ax2=bx+c的解 为: ;
故答案为: 。
【分析】求关于x的方程ax2=bx+c的解 就是抛物线y=ax2和直线y=bx+c的两个交点的横坐标。
19.【答案】 C
【解析】【解答】解:对于抛物线 ,
当 时, ,解得 或 ,
则 ,
的面积为3,
,即 ,解得 ,
,
将点 代入抛物线解析式得: ,解得 ,
则抛物线的解析式为 ,
将抛物线向左平移 个单位所得抛物线为 ,
当 时, 随 的增大而增大,
设直线 的函数解析式 ,
将点 代入得: ,解得 ,
则直线 的函数解析式 ,
当直线 与 没有公共点时,则只需 时,直线 的函数值大于抛物线 的函数值,
即 ,
解得 ,
故答案为:C.
【分析】先根据抛物线的解析式可得点 A,B 的坐标,从而可得 AB 长,再利用三角形的面积公式可得 OC 的长,从而可得点 C 的坐标,利用待定系数法可求出抛物线的解析式和一次函数的解析式,然后根据二次函数图象的平移规律、增减性求解即可得.
20.【答案】 A
【解析】【解答】解:∵ 抛物线与x轴交于点(-1, 0), 抛物线与直线交点的横坐标为1和
∴ 不等式mx+n <ax2+bx+c <0的解集为:1<x<2
【分析】根据已知条件: 抛物线与x轴交于点(-1, 0), 抛物线与直线交点的横坐标为1和 , 观察函数图像可得出不等式mx+n <ax2+bx+c <0的解集。
21.【答案】 (1)解:将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1,所以二次函数解析式为y=(x-2)2-1;当x=0时,y=4-1=3,所以C点坐标为(0,3),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,
所以B点坐标为(4,3),将A(1,0)、B(4,3)代入y=kx+b得 ,解得 ,
所以一次函数解析式为y=x-1;
(2)解:观察图象可得x的取值范围:x≤1或x≥4.
【解析】【分析】(1)将点A代入二次函数解析式,求出m的值,可得出二次函数解析式,求出点C的坐标,再根据C和B关于对称轴对称,可得出点B的坐标,然后利用待定系数法求出一次函数解析式。
(2)观察直线x=1和直线x=4时,写出一次函数的图像低于二次函数的图像时的x的取值范围。
22.【答案】 (1)4a
(2)解:当a = -1时,∵关于x的方程 在-3< x <1的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,∴b2 -4ac =16+4c ≥0,即c ≥ -4.
∴抛物线y= x2 +4x=(x+2)2 -4与直线y = c在-3
故可得: -4≤ c< 5.
(3)解:∵抛物线y=ax2+4ax+c过点(-2,-2),∴c = 4a -2.∴抛物线解析式为: .
① 当a > 0时,抛物线开口向上.
∵抛物线对称轴为x=-2.
∴当-1≤x≤0时,y随x增大而增大.
∵抛物线上的点到x轴距离的最大值为4,
由图像可知:4a -2=4.
∴ .
② 当a < 0时,抛物线开口向下.
∵抛物线对称轴为x=-2.∴当-1≤x≤0时,y随x增大而减小.∵抛物线上的点到x轴距离的最大值为4,由图像可知:4a -2= -4.∴ . 综上所述: .
【解析】【解答】解:(1)∵抛物线 (a、b、c是常数, )的对称轴为直线 ,
∴ ,
∴b=4a ;
【分析】(1)根据抛物线的对称轴公式即可得出,故b=4a ;
(2)当a= 1 时,若关于x的方程 ax2+bx+c=0 在 3 < x < 1 的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,从函数图像的观点看,则抛物线y= x2 +4x=(x+2)2 -4与直线y = -c在-3
23.【答案】 (1)解: ;;
(2)解:函数y=x2-2x-3的图象如图2所示,
∵A(-1,0),B(3,0),
∴不等式x2-2x-3≥0的解集,由图象可知,x≥3或x≤-1
【解析】【解答】(1)二次函数y=x2-2x的图象如图1所示,
∵二次函数y=x2-2x与x轴交于O(0,0),A(2,0),
∴方程x2-2x=0的解为x=0或2.
由图象可知x2-2x<0的解集为0<x<2.
故答案为x=0或2,0<x<2.
【分析】(1)① 画出二次函数y= x2 2x的图像即可;②求出当y=0时的自变量x的值,用虚线画出x轴下方的抛物线;③观察x轴下方的函数图像,利用抛物线与x轴的两交点坐标,可得出不等式 x2 2x <0的解集。
(2)画出抛物线y=x2 2x -3的大致图像,再求出此抛物线与x轴的交点A、B的坐标,再观察x轴上方的函数图像,可得出答案。
21世纪教育网(www.21cnjy.com)
同课章节目录
