2022-2023学年浙教版八年级数学上册1.5 三角形全等的判定 解答题专题训练 (word、含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册1.5 三角形全等的判定 解答题专题训练 (word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 444.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 18:56:20 | ||
图片预览


文档简介
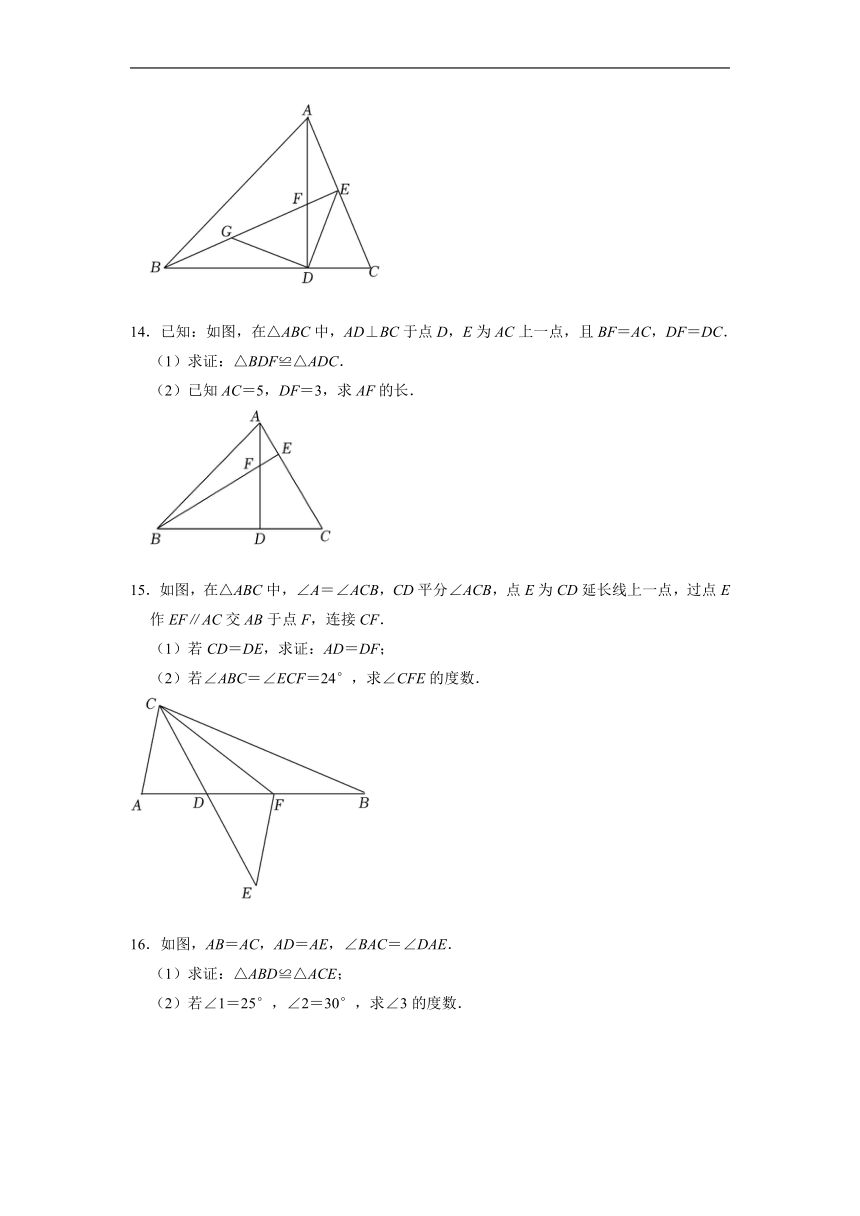
2022-2023年浙教版八年级数学上册《1.5三角形全等的判定》解答题专题训练(附答案)
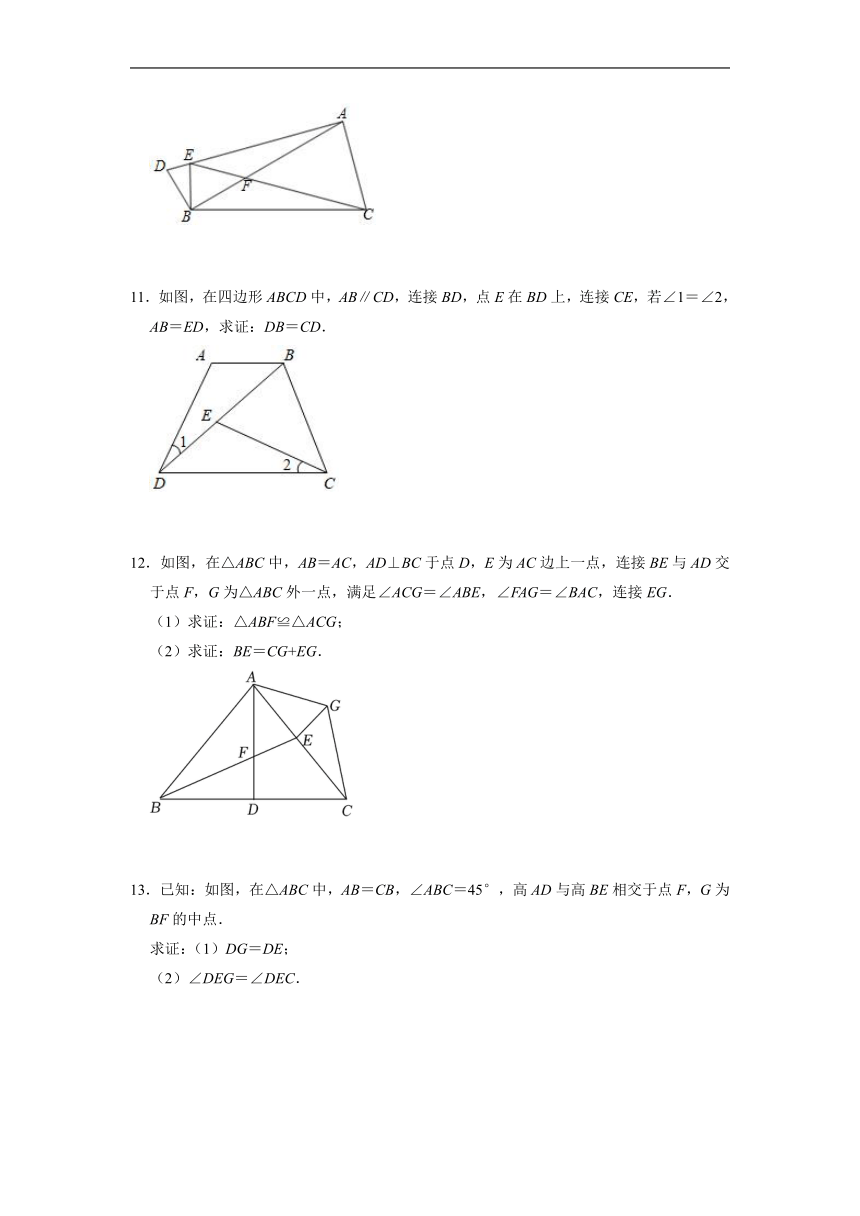
1.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
2.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
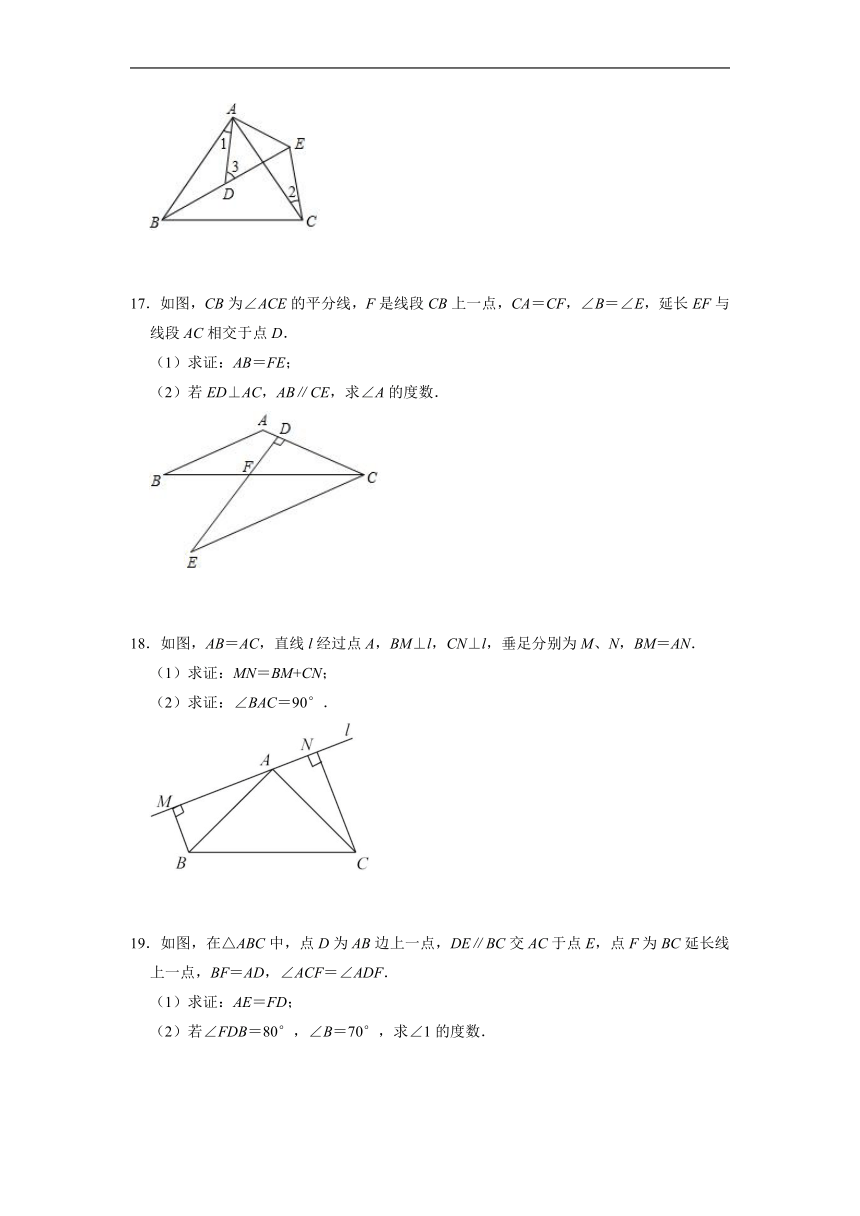
求证:BC=BE.
3.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
4.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
求证:Rt△ABE≌Rt△CBF.
5.如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
6.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.
求证:OB=OC.
7.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
8.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
9.已知:点A,D,C,B在同一条直线上,DF∥CE,DF=CE,AD=BC.
求证:(1)CF=DE;
(2)AF∥EB.
10.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
11.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
12.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
13.已知:如图,在△ABC中,AB=CB,∠ABC=45°,高AD与高BE相交于点F,G为BF的中点.
求证:(1)DG=DE;
(2)∠DEG=∠DEC.
14.已知:如图,在△ABC中,AD⊥BC于点D,E为AC上一点,且BF=AC,DF=DC.
(1)求证:△BDF≌△ADC.
(2)已知AC=5,DF=3,求AF的长.
15.如图,在△ABC中,∠A=∠ACB,CD平分∠ACB,点E为CD延长线上一点,过点E作EF∥AC交AB于点F,连接CF.
(1)若CD=DE,求证:AD=DF;
(2)若∠ABC=∠ECF=24°,求∠CFE的度数.
16.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
17.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
18.如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
19.如图,在△ABC中,点D为AB边上一点,DE∥BC交AC于点E,点F为BC延长线上一点,BF=AD,∠ACF=∠ADF.
(1)求证:AE=FD;
(2)若∠FDB=80°,∠B=70°,求∠1的度数.
20.已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
21.已知:如图,AD、BF相交于O点,OA=OD,AB∥DF,点E、C在BF上,BE=CF.
(1)求证:△ABO≌△DFO;
(2)判断线段AC、DE的关系,并说明理由.
22.如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=5,CF=7,求DB的长.
参考答案
1.证明:∵∠A=∠D=90°,AC=BD,BC=BC,
∴Rt△BAC≌Rt△CDB(HL)
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
2.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
3.证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中
,
∴Rt△ABC≌Rt△DEF(HL).
4.证明:在Rt△ABE和Rt△CBF中,
∵,
∴Rt△ABE≌Rt△CBF(HL).
5.证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.
∴∠ABD=∠DAC.
∵在△ABD和△CAE中
,
∴△ABD≌△CAE(AAS).
∴BD=AE,EC=AD.
∵AE=AD+DE,
∴BD=EC+ED.
6.证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,
∴∠1=∠2.
在△AOD和△AOE中,,
∴△AOD≌△AOE(AAS).
∴OD=OE.
在△BOD和△COE中,,
∴△BOD≌△COE(ASA).
∴OB=OC.
7.证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
8.证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
9.证明:(1)∵DF∥CE,
∴∠FDC=∠ECD,
在△FDC和△ECD中,
,
∴△FDC≌△ECD(SAS),
∴CF=DE;
(2)∵△FDC≌△ECD,
∴∠FCD=∠EDC,
∵AD=BC,
∴AD+DC=BC+DC,
∴AC=BD,
在△FAC和△EBD中,
,
∴△FAC≌△EBD(SAS),
∴∠A=∠B,
∴AF∥EB.
10.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠ABE=∠DBE+∠ABE,
∴∠ABD=∠CBE.
在△ADB和△CEB中,
,
∴△ADB≌△CEB(SAS),
∴AD=CE;
(2)解:∵BA=BC,∠ABC=30°,
∴∠BAC=∠BCA=(180°﹣30°)=75°,
∵∠AFC=45°,
∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,
∵△ADB≌△CEB,
∴∠BAD=∠BCE=15°,
∴∠EAC=∠BAD+∠BAC=15°+75°=90°.
11.证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.
12.(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAG,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
13.证明:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
,
∴△BDF≌△ACD(AAS),
∴BF=AC,
∵G为BF的中点.
∴DG=BF,
∵AB=CB,BE⊥AC,
∴E为AC的中点.
∴DE=AC,
∴DG=DE;
(2)由(1)知:∠DBG=∠DAE,BG=BF,AE=AC,BF=AC,
∴BG=AE,
在△BDG和△ADE中,
,
∴△BDG≌△ADE(SAS),
∴∠BDG=∠ADE,
∴∠DGB=∠DBG+∠BDG,
∵∠DEC=∠DAE+∠ADE,
∴∠DGB=∠DEC,
∵DG=DE,
∴∠DGE=∠DEG,
∴∠DEG=∠DEC.
14.(1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△BDF和Rt△ADC中,
,
∴Rt△BDF≌Rt△ADC(HL).
(2)解:∵Rt△BDF≌Rt△ADC,
∴DC=DF.
在Rt△ADC中,(AF+3)2+32=52,
∴AF=1或AF=7(舍)
∴AF=1.
15.(1)证明:∵EF∥AC,
∴∠A=∠EFD,∠ACD=∠E,
在△ADC和△FDE中,
,
∴△ADC≌△FDE(AAS),
∴AD=DF;
(2)解:∵∠A=∠ACB,∠ABC=∠ECF=24°,
∴∠A=∠ACB==78°,
∵CD平分∠ACB,
∴∠ACE=∠BCE=39°,
∵EF∥AC,
∴∠A=∠EFD=78°,∠ACD=∠E=39°,
∵∠ECF=24°,
∴∠CFE=180°﹣∠ECF﹣∠E=180°﹣24°﹣39°=117°.
16.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
17.证明:(1)∵CB为∠ACE的角平分线,
∴∠ACB=∠FCE,
在△ABC与△FEC中,
,
∴△ABC≌△FEC(AAS),
∴AB=FE;
(2)∵AB∥CE,
∴∠B=∠FCE,
∴∠E=∠B=∠FCE=∠ACB,
∵ED⊥AC,即∠CDE=90°,
∴∠E+∠FCE+∠ACB=90°,
即3∠ACB=90°,
∴∠ACB=30°,
∴∠B=30°,
∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.
18.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL),
∴BM=AN,CN=AM,
∴MN=AM+AN=BM+CN;
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
19.(1)证明:∵∠ACF=∠ADF,
∴∠B+∠A=∠B+∠F,
∴∠A=∠F,
∵DE∥BC,
∴∠ADE=∠B,
在△ADE和△FBD中,
,
∴△ADE≌△FBD(ASA),
∴AE=FD;
(2)解:∵∠FDB=80°,∠B=70°,
∴∠F=30°,
∴∠ACF=∠ADF=∠B+∠F=100°,
∴∠1=∠F+∠ACF=130°.
20.解:(1)∵BD⊥AC,CE⊥AB,
∴∠ADB=∠BDC=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABD和△FCD中,
,
∴△ABD≌△FCD(ASA),
∴AB=CF,
∵CE平分∠ACB,
∴∠ACE=∠BCE=22.5°,
在△ACE和△BCE中,
,
∴△ACE≌△BCE(ASA),
∴AE=BE,
∴BE=AB=CF;
(2)BN=MG,
理由如下:如图,过点M作MH∥AC,交AB于H,交BD于P,
∵BD=CD,BD⊥CD,
∴∠DBC=∠DCB=45°,
∵MH∥AC,
∴∠PMB=∠DCB=∠PBM=45°,∠BPM=∠BDC=90°,
∴BP=PM,
∵∠BHP+∠HBP=90°,∠BHP+∠HMN=90°,
∴∠HBP=∠HMN,
在△BHP和△MGP中,
,
∴△BPH≌△MPG(ASA),
∴GM=BH,
∵MN⊥AB,CE⊥AB,
∴MN∥CE,
∴∠BMN=∠BCE=∠ACB=22.5°,
∴∠BMN=∠HMN=22.5°,
在△BMN和△HMN中,
,
∴△BMN≌△HMN(ASA)
∴BN=NH,
∴BN=BH=MG.
21.(1)证明:∵AB∥DF,
∴∠B=∠F,∠BAO=∠FDO,
在△ABO和△DFO中,
,
∴△ABO≌△DFO(AAS);
(2)解:AC=DE,AC∥DE,理由如下:
∵△ABO≌△DFO,
∴BO=FO,
∵BE=CF,
∴EO=CO,
在△AOC和△DOE中,
,
∴△AOC≌△DOE(SAS),
∴AC=DE,∠DAC=∠ADE,
∴AC∥DE.
22.(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS).
(2)解:∵△ADE≌△CFE,CF=7,
∴CF=AD=7,
∵AB=AC,E是边AC的中点,CE=5,
∴AC=2CE=10.
∴AB=10,
∴DB=AB﹣AD=10﹣7=3.
1.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
2.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
3.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
4.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
求证:Rt△ABE≌Rt△CBF.
5.如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
6.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.
求证:OB=OC.
7.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
8.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
9.已知:点A,D,C,B在同一条直线上,DF∥CE,DF=CE,AD=BC.
求证:(1)CF=DE;
(2)AF∥EB.
10.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
11.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
12.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.
(1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
13.已知:如图,在△ABC中,AB=CB,∠ABC=45°,高AD与高BE相交于点F,G为BF的中点.
求证:(1)DG=DE;
(2)∠DEG=∠DEC.
14.已知:如图,在△ABC中,AD⊥BC于点D,E为AC上一点,且BF=AC,DF=DC.
(1)求证:△BDF≌△ADC.
(2)已知AC=5,DF=3,求AF的长.
15.如图,在△ABC中,∠A=∠ACB,CD平分∠ACB,点E为CD延长线上一点,过点E作EF∥AC交AB于点F,连接CF.
(1)若CD=DE,求证:AD=DF;
(2)若∠ABC=∠ECF=24°,求∠CFE的度数.
16.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
17.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
18.如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
19.如图,在△ABC中,点D为AB边上一点,DE∥BC交AC于点E,点F为BC延长线上一点,BF=AD,∠ACF=∠ADF.
(1)求证:AE=FD;
(2)若∠FDB=80°,∠B=70°,求∠1的度数.
20.已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
21.已知:如图,AD、BF相交于O点,OA=OD,AB∥DF,点E、C在BF上,BE=CF.
(1)求证:△ABO≌△DFO;
(2)判断线段AC、DE的关系,并说明理由.
22.如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,CE=5,CF=7,求DB的长.
参考答案
1.证明:∵∠A=∠D=90°,AC=BD,BC=BC,
∴Rt△BAC≌Rt△CDB(HL)
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
2.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
3.证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中
,
∴Rt△ABC≌Rt△DEF(HL).
4.证明:在Rt△ABE和Rt△CBF中,
∵,
∴Rt△ABE≌Rt△CBF(HL).
5.证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.
∴∠ABD=∠DAC.
∵在△ABD和△CAE中
,
∴△ABD≌△CAE(AAS).
∴BD=AE,EC=AD.
∵AE=AD+DE,
∴BD=EC+ED.
6.证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,
∴∠1=∠2.
在△AOD和△AOE中,,
∴△AOD≌△AOE(AAS).
∴OD=OE.
在△BOD和△COE中,,
∴△BOD≌△COE(ASA).
∴OB=OC.
7.证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
8.证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
9.证明:(1)∵DF∥CE,
∴∠FDC=∠ECD,
在△FDC和△ECD中,
,
∴△FDC≌△ECD(SAS),
∴CF=DE;
(2)∵△FDC≌△ECD,
∴∠FCD=∠EDC,
∵AD=BC,
∴AD+DC=BC+DC,
∴AC=BD,
在△FAC和△EBD中,
,
∴△FAC≌△EBD(SAS),
∴∠A=∠B,
∴AF∥EB.
10.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠ABE=∠DBE+∠ABE,
∴∠ABD=∠CBE.
在△ADB和△CEB中,
,
∴△ADB≌△CEB(SAS),
∴AD=CE;
(2)解:∵BA=BC,∠ABC=30°,
∴∠BAC=∠BCA=(180°﹣30°)=75°,
∵∠AFC=45°,
∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,
∵△ADB≌△CEB,
∴∠BAD=∠BCE=15°,
∴∠EAC=∠BAD+∠BAC=15°+75°=90°.
11.证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.
12.(1)证明:∵∠BAC=∠FAG,
∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,
∴∠BAD=∠CAG,
在△ABF和△ACG中,
,
∴△ABF≌△ACG(ASA);
(2)证明:∵△ABF≌△ACG,
∴AF=AG,BF=CG,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAG,
∵∠BAD=∠CAG,
∴∠CAD=∠CAG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS).
∴EF=EG,
∴BE=BF+FE=CG+EG.
13.证明:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
,
∴△BDF≌△ACD(AAS),
∴BF=AC,
∵G为BF的中点.
∴DG=BF,
∵AB=CB,BE⊥AC,
∴E为AC的中点.
∴DE=AC,
∴DG=DE;
(2)由(1)知:∠DBG=∠DAE,BG=BF,AE=AC,BF=AC,
∴BG=AE,
在△BDG和△ADE中,
,
∴△BDG≌△ADE(SAS),
∴∠BDG=∠ADE,
∴∠DGB=∠DBG+∠BDG,
∵∠DEC=∠DAE+∠ADE,
∴∠DGB=∠DEC,
∵DG=DE,
∴∠DGE=∠DEG,
∴∠DEG=∠DEC.
14.(1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△BDF和Rt△ADC中,
,
∴Rt△BDF≌Rt△ADC(HL).
(2)解:∵Rt△BDF≌Rt△ADC,
∴DC=DF.
在Rt△ADC中,(AF+3)2+32=52,
∴AF=1或AF=7(舍)
∴AF=1.
15.(1)证明:∵EF∥AC,
∴∠A=∠EFD,∠ACD=∠E,
在△ADC和△FDE中,
,
∴△ADC≌△FDE(AAS),
∴AD=DF;
(2)解:∵∠A=∠ACB,∠ABC=∠ECF=24°,
∴∠A=∠ACB==78°,
∵CD平分∠ACB,
∴∠ACE=∠BCE=39°,
∵EF∥AC,
∴∠A=∠EFD=78°,∠ACD=∠E=39°,
∵∠ECF=24°,
∴∠CFE=180°﹣∠ECF﹣∠E=180°﹣24°﹣39°=117°.
16.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
17.证明:(1)∵CB为∠ACE的角平分线,
∴∠ACB=∠FCE,
在△ABC与△FEC中,
,
∴△ABC≌△FEC(AAS),
∴AB=FE;
(2)∵AB∥CE,
∴∠B=∠FCE,
∴∠E=∠B=∠FCE=∠ACB,
∵ED⊥AC,即∠CDE=90°,
∴∠E+∠FCE+∠ACB=90°,
即3∠ACB=90°,
∴∠ACB=30°,
∴∠B=30°,
∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.
18.证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL),
∴BM=AN,CN=AM,
∴MN=AM+AN=BM+CN;
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
19.(1)证明:∵∠ACF=∠ADF,
∴∠B+∠A=∠B+∠F,
∴∠A=∠F,
∵DE∥BC,
∴∠ADE=∠B,
在△ADE和△FBD中,
,
∴△ADE≌△FBD(ASA),
∴AE=FD;
(2)解:∵∠FDB=80°,∠B=70°,
∴∠F=30°,
∴∠ACF=∠ADF=∠B+∠F=100°,
∴∠1=∠F+∠ACF=130°.
20.解:(1)∵BD⊥AC,CE⊥AB,
∴∠ADB=∠BDC=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABD和△FCD中,
,
∴△ABD≌△FCD(ASA),
∴AB=CF,
∵CE平分∠ACB,
∴∠ACE=∠BCE=22.5°,
在△ACE和△BCE中,
,
∴△ACE≌△BCE(ASA),
∴AE=BE,
∴BE=AB=CF;
(2)BN=MG,
理由如下:如图,过点M作MH∥AC,交AB于H,交BD于P,
∵BD=CD,BD⊥CD,
∴∠DBC=∠DCB=45°,
∵MH∥AC,
∴∠PMB=∠DCB=∠PBM=45°,∠BPM=∠BDC=90°,
∴BP=PM,
∵∠BHP+∠HBP=90°,∠BHP+∠HMN=90°,
∴∠HBP=∠HMN,
在△BHP和△MGP中,
,
∴△BPH≌△MPG(ASA),
∴GM=BH,
∵MN⊥AB,CE⊥AB,
∴MN∥CE,
∴∠BMN=∠BCE=∠ACB=22.5°,
∴∠BMN=∠HMN=22.5°,
在△BMN和△HMN中,
,
∴△BMN≌△HMN(ASA)
∴BN=NH,
∴BN=BH=MG.
21.(1)证明:∵AB∥DF,
∴∠B=∠F,∠BAO=∠FDO,
在△ABO和△DFO中,
,
∴△ABO≌△DFO(AAS);
(2)解:AC=DE,AC∥DE,理由如下:
∵△ABO≌△DFO,
∴BO=FO,
∵BE=CF,
∴EO=CO,
在△AOC和△DOE中,
,
∴△AOC≌△DOE(SAS),
∴AC=DE,∠DAC=∠ADE,
∴AC∥DE.
22.(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS).
(2)解:∵△ADE≌△CFE,CF=7,
∴CF=AD=7,
∵AB=AC,E是边AC的中点,CE=5,
∴AC=2CE=10.
∴AB=10,
∴DB=AB﹣AD=10﹣7=3.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
