全等三角形

1．4 全等三角形
【知识提要】
1．会说出怎样的两个图形是全等图形，并会用符号语言表示两个三角形全等．
2．知道全等三角形的有关概念，会在全等三角形中正确找出对应顶点、对应边、对应角．
3．会说出对应边、对应角相等的性质．
【学法指导】
1．两个三角形的全等是指两个图形之间的一种对应关系，对应关系是按一定标准的一对一的关系，“互相重合”是判断其对应部分的标准．
2．实际遇到的图形，两个全等三角形并不重合在一起，但其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法得到的．
范例积累
【例1】 如图，△ABD≌△CDB，且AB、CD是对应边，下面四个结论中不正确的是（ ）
A．△ABD和△CDB的面积相等
B．△ABD和△CDB的周长相等
C．∠A+∠ABD=∠C+∠CBD
D．AD∥BC且AD=BC
【分析】 由于两个三角形完全重合，故面积周长相等，对应角对应边相等，而∠ABD与∠CBD不是对应角，所以C符号题意．
【解】 选C．
如图，已知△ABC≌△ADE，试找出对应边、对应角．
【分析】 连结AO，将△ABC沿AO翻折180°，即可得到△ADE，对应元素易找，找对应元素常利用“运动法”来找．
a．翻折法：找到中心线，经此翻折后能互相重合的两个三角形，易发现其对应元素．
b．旋转法：两个三角形绕某一点旋转一定角度能够重合时，易于找到对应元素．
c．平移法：将两个三角形沿某一直线推移重合时也可找到对应元素．
【解】 对应角：∠A=∠A、∠B=∠D、∠ACB=∠AED
对应边：AB=AD、BC=DE、AC=AE．
如图，已知△ACF≌△DBE，∠E=∠F，AD=9cm，BC=5cm，求AB的长．
【分析】 AB不是全等三角形的对应边，但它通过对应边转化为AB=CD而AB+CD=AD-BC，可利用已知的AD与BC求得．
【解】 ∵△ACF≌△DBE，∴∠E=∠F
∴AC-BC=DB-BC，即AB=CD
∴AB+CD=2AB=AD-BC=9-5=4（cm）
∴AB=2（cm）
基础训练
1．下列说法正确的是（ ）
A．全等三角形是指形状相同的两个三角形；
B．全等三角形是指面积相等的两个三角形
C．全等三角形的周长和面积分别相等；
D．所有等边三角形都是全等三角形
2．已知△ABC与△DEF全等，∠B与∠F，∠C与∠E是对应角，那么①BC=EF；②∠C的平分线与∠E的平分线相等；③AC边上的高与DE边上的高相等；④AB边上的中线与DE边上的中线相等．其中正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
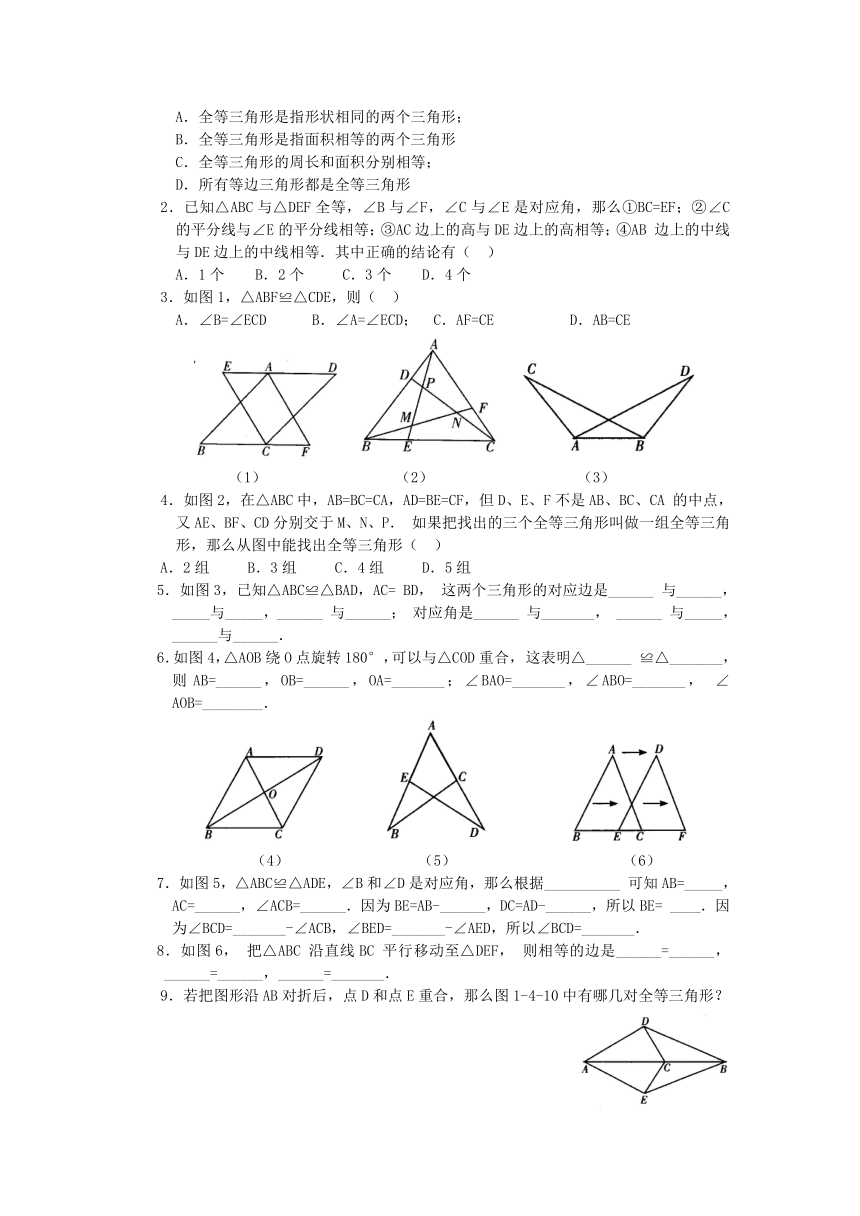
3．如图1，△ABF≌△CDE，则（ ）
A．∠B=∠ECD B．∠A=∠ECD； C．AF=CE D．AB=CE
（1） （2） （3）
4．如图2，在△ABC中，AB=BC=CA，AD=BE=CF，但D、E、F不是AB、BC、CA的中点，又AE、BF、CD分别交于M、N、P．如果把找出的三个全等三角形叫做一组全等三角形，那么从图中能找出全等三角形（ ）
A．2组 B．3组 C．4组 D．5组
5．如图3，已知△ABC≌△BAD，AC=BD，这两个三角形的对应边是______与______，_____与_____，______与______；对应角是______与_______，______与_____，______与______．
6．如图4，△AOB绕O点旋转180°，可以与△COD重合，这表明△______≌△_______，则AB=______，OB=______，OA=_______；∠BAO=_______，∠ABO=_______，∠AOB=________．
（4） （5） （6）
7．如图5，△ABC≌△ADE，∠B和∠D是对应角，那么根据__________可知AB=_____，AC=______，∠ACB=______．因为BE=AB-______，DC=AD-______，所以BE=____．因为∠BCD=_______-∠ACB，∠BED=_______-∠AED，所以∠BCD=_______．
8．如图6，把△ABC沿直线BC平行移动至△DEF，则相等的边是______=______，______=______，______=_______．
9．若把图形沿AB对折后，点D和点E重合，那么图1-4-10中有哪几对全等三角形？
10．如图，△ABC≌△DEF，AB和DE是对应边，∠A和∠D是对应角，找出图中所有相等的线段和角．
提高训练
11．如图，把大小为4×4的正方形方格图分割成两个全等图形，例如图1，请在下图中沿着虚线画出四种不同的方法，把4×4的正方形方格图分割成两个全等图形．
12．如图，已知四边形纸片ABCD中，AD∥BC，将△ABC、∠DAB分别对折．如果两条折痕恰好相交于DC上一点E，且C和D均落在F点，你能获得哪些结论？
应用拓展
13．如图，把△ABC绕点C顺时针旋转35°，得到△A′B′C′，A′B′交AC于D，已知∠A′DC=90°，求∠A的度数．
答案：
1．C 2．C 3．C 4．D
5．AB BA AC BD AD BC ∠C ∠D ∠CAB  ∠DBA ∠CBA ∠DAB
6．AOB COD CD OD OC ∠DCO ∠CDO ∠COD
7．全等三角形性质 AD AE ∠AED AE AC CD 180° 180° ∠BED
8．AB=DE  AC=DF BC=EF
9．△DCB与△ECB △ADB与△AEB △ADC与△AEC
10．AB=DE AC=DF BC=EF AF=CD ∠A=∠D ∠B=∠E ∠ACB=∠DFE ∠BCD=∠AFE 11．略 12．△BCE≌△BFE △AED≌△AEF BF=CB CE=EF=DE AD=AF
∠1=∠2 ∠3=∠4 ∠D=∠EFA ∠CEB=∠BEF ∠C=∠EFB ∠DEA=∠FEA
13．△ABC≌△A′B′C′ ∠A′C′B=∠ACB，
而∠BCB′=35°，得∠A′CD=35°，
又∠A′+∠A′CD=90°，则∠A′=∠A=55°