1.5三角形全等的条件（一）

1．5 三角形全等的条件（一）
【知识提要】
1．掌握已知三边画三角形的方法．
2．掌握边边边公理，能用边边边公理说明两个三角形全等．
3．了解三角形的稳定性．
【学法指导】
1．在公理形成过程中学会实验、观察、归纳．
2．通过几何说明养成尊重客观事实、形成质疑的习惯．
范例积累
【例1】 下列判断，其中正确的是（ ）
A．三个角对应相等的两个三角形全等
B．周长相等的两个三角形全等
C．周长相等的两个等边三角形全等
D．有两边和第三边上的高对应相等的两个三角形全等
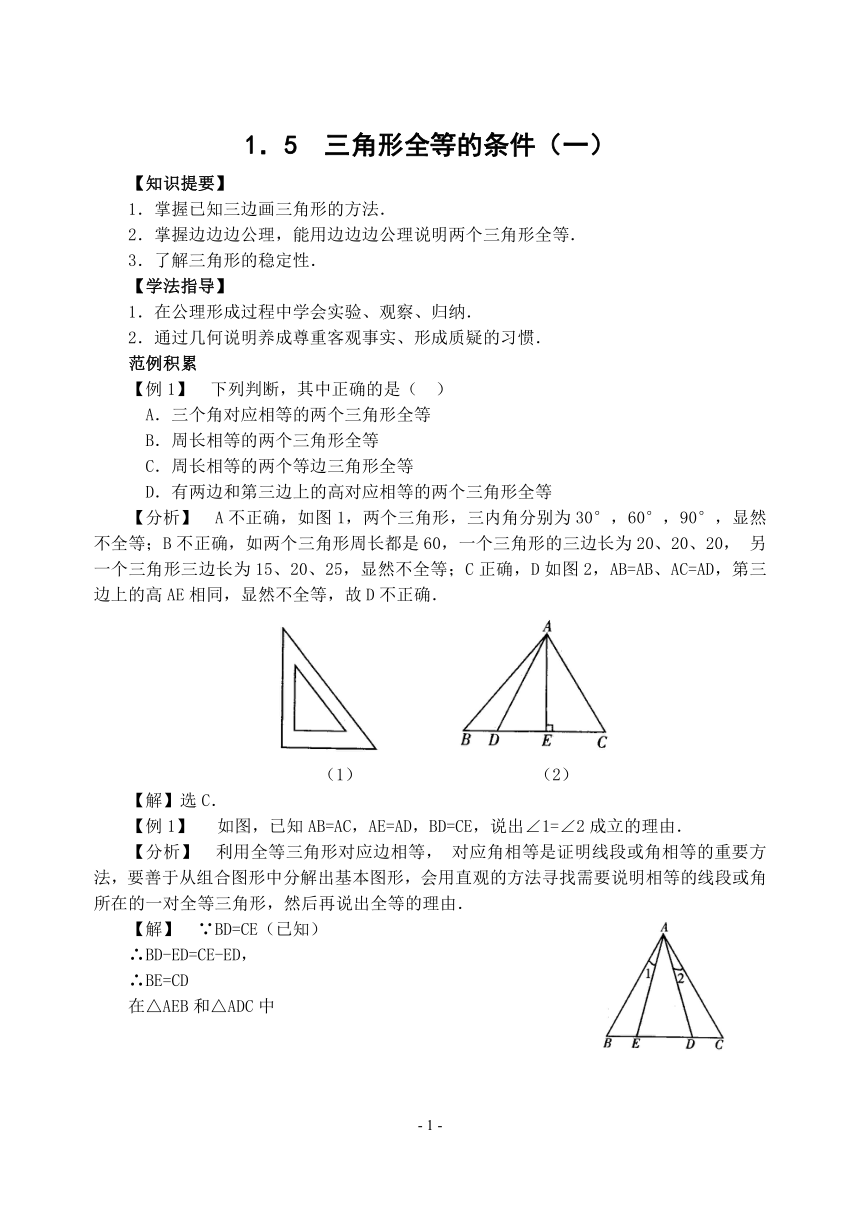
【分析】 A不正确，如图1，两个三角形，三内角分别为30°，60°，90°，显然不全等；B不正确，如两个三角形周长都是60，一个三角形的三边长为20、20、20，另一个三角形三边长为15、20、25，显然不全等；C正确，D如图2，AB=AB、AC=AD，第三边上的高AE相同，显然不全等，故D不正确．
（1） （2）
【解】选C．
如图，已知AB=AC，AE=AD，BD=CE，说出∠1=∠2成立的理由．
【分析】 利用全等三角形对应边相等，对应角相等是证明线段或角相等的重要方法，要善于从组合图形中分解出基本图形，会用直观的方法寻找需要说明相等的线段或角所在的一对全等三角形，然后再说出全等的理由．
【解】 ∵BD=CE（已知）
∴BD-ED=CE-ED，
∴BE=CD
在△AEB和△ADC中
∴△AEB≌△ADC（SSS）
∴∠1=∠2（全等三角形对应角相等）．
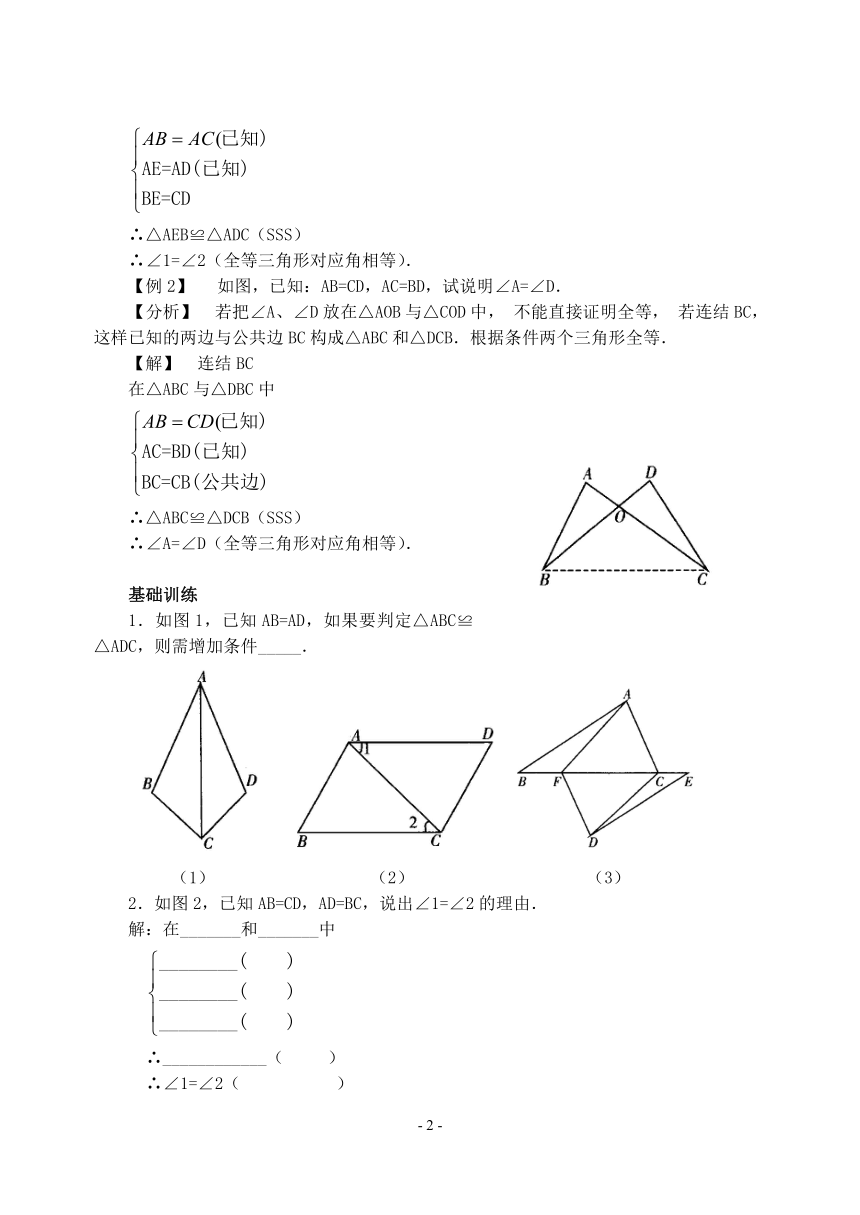
如图，已知：AB=CD，AC=BD，试说明∠A=∠D．
【分析】 若把∠A、∠D放在△AOB与△COD中，不能直接证明全等，若连结BC，这样已知的两边与公共边BC构成△ABC和△DCB．根据条件两个三角形全等．
【解】 连结BC
在△ABC与△DBC中
∴△ABC≌△DCB（SSS）
∴∠A=∠D（全等三角形对应角相等）．
基础训练
1．如图1，已知AB=AD，如果要判定△ABC≌△ADC，则需增加条件_____．
（1） （2） （3）
2．如图2，已知AB=CD，AD=BC，说出∠1=∠2的理由．
解：在_______和_______中
∴____________（ ）
∴∠1=∠2（ ）
3．如图3，已知△ABF≌△DEC，且AC=DF，说明△ABC≌△DEF的理由．
解：∵△ABF≌△DEC
∴AB=________ BF=________
又∵BC=BF+_________，EF=CE+________．
∴BC=_________．
在△ABC与△DEF中
∴△ABC≌△DEF（ ）
4．如图4，已知AB=CD，AE=CF，若再满足________，或_______，或△______≌△______就可证明△ABE≌△CDF．
5．如图1-5-9，已知AD=BC，OD=OC，O为AB中点，说出△AOD≌△BOC的理由．
6．如图，△ABC和△DBC中，AB=CD，AC=BD，AC和DB相交于O，说出∠1=∠2的理由．
7．如图，AE=BF，CE=DF，AB=CD，说出CE∥DF的理由．
提高训练
8．如图，AB=DB，AC=DC，DH⊥BC于H，若∠ABC=65°，求∠BDH的度数．
9．如图，已知AB=CD，AD=CB，E、F分别是AB、CD的中点，且AF=CE，找出图中的全等三角形，并说明理由．
应用拓展
10．如图，AC=AD，BC=BD，试说明∠C=∠D．
11．如图，四边形ABCD中，AB=CD，AD=CB，你能通过添画线段，把它分成两个全等三角形吗？有几种添法？
答案：
1．BC=CD
2．△ABC △CDA AB=CD（已知） AD=BC（已知） AC=CA（公共边）
△ABC≌△CDA（SSS） 全等三角形对应角相等
3．DE CE CF
4．BE=DF BF=DE △AED≌△CFB
5．∵AO=BO AD=BC OD=OC
∴△AOD≌△BOC（SSS）
6．∵AB=CD AC=BD BC=CB
∴△ABC≌△DCB（SSS）
∴∠ABC=∠DCB ∠DBC=∠ACB
∴∠1=∠2 
7．∵AB=CD ∴AC=BD
又∵AE=BF CE=DF ∴△AEC≌△BFD
∴∠ECB=∠D ∴EC∥DF
8．AB=DB AC=DC BC=BC
∴△ABC≌△DBC
∴∠ABC=∠CBD=65°
∵DH⊥BC
∴∠DHB=90°
∴∠BDH=25°
9．△AFD≌△CEB ≌ △FAE≌△ECF
10．连结AB ∵AC=AD BC=BD AB=AB
∴△ABC≌△ABD ∴∠C=∠D
11．连结BD则△ADB≌△CBD，连结AC，则△ADC≌△CBA。
（4）
- 1 -