1.5三角形全等的条件（二）

1．5 三角形全等的条件（二）
【知识提要】
1．掌握边角边公理的内容．
2．能应用边角边公理证明两个三角形全等．
3．掌握线段垂直平分线的性质定理，并能应用它证明线段相等．
【学法指导】
1．边角边公理中相等的角必须是夹角，要注意两边及其中一边的对角对应相等的两个三角形不一定全等．
2．由边角边公理得出线段中垂线的性质定理，通过知识的纵横迁移感受数学的辩证特征．
范例积累
【例1】 如图1-5-16，BD、AC交于O，若OA=OD，用“SAS”证△AOB≌△DOC还需（ ）
A．AB=DC B．OB=OC
C．∠A=∠D D．∠AOB=∠DOC
【分析】 用“SAS”证全等有三个独立条件，已知OA=OD，显然还差两个，由AC、BD相交可得∠AOB与∠DOC是一对对顶角，第三个条件应该围绕夹角∠AOB、∠DOC找，显然OB与OC应是另一组夹边．
【解】 选B．
【例2】 如图，已知AB、CD相交于O，△ACO≌△BDO，AE=BF，试说明CE=FD．
【分析】 本题考查SAS公理的应用，要证CE=FD，只要证△OCE≌△ODF．显然∠EOC=∠FOD．需证OE=OF，OC=OD．因AE=BF，故需证OA=OB，由已知△ACO≌△BDO，可得OC=OD，OA=OB．
【解】 ∵△ACO≌△BDO
∴CO=DO，AO=BO
∵AE=BF，∴EO=FO
在△EOC与△FOD中

∴△EOC≌△FOD，∴EC=FD
【例3】 如图，在△ABC中，AD为BC边上中线．试说明AD<（AB+AC）．
【分析】 证明边之间的关系一般是在一个三角形中利用“三角形边的关系推论”，所以考虑把线段AB、AD、AC的等价线段放在一个三角形中．因此需添加辅助线，而涉及到一边的中线问题需要引辅助线，常用方法：延长中线使之延长后的线段与中线相等并连结，构造成两个三角形全等．
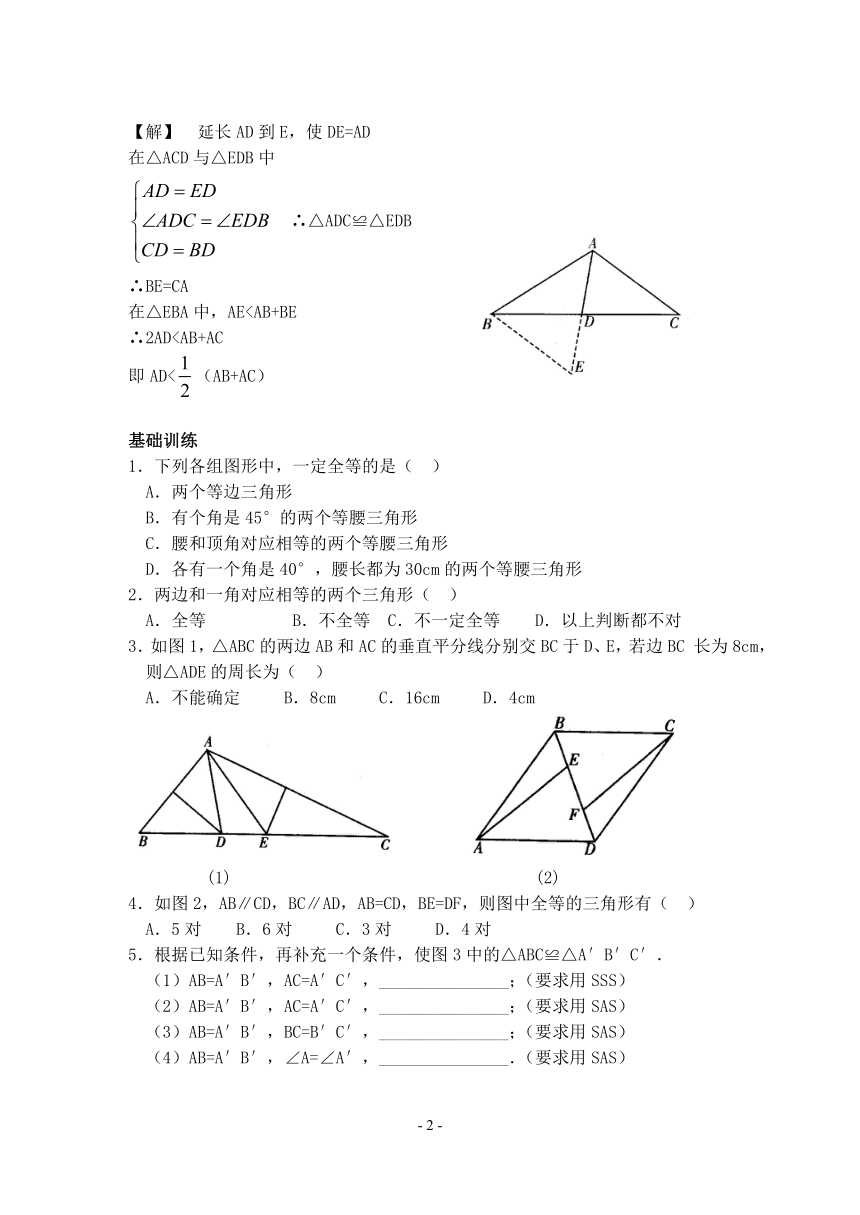
【解】 延长AD到E，使DE=AD
在△ACD与△EDB中
∴△ADC≌△EDB
∴BE=CA
在△EBA中，AE ∴2AD 即AD<（AB+AC）
基础训练
1．下列各组图形中，一定全等的是（ ）
A．两个等边三角形
B．有个角是45°的两个等腰三角形
C．腰和顶角对应相等的两个等腰三角形
D．各有一个角是40°，腰长都为30cm的两个等腰三角形
2．两边和一角对应相等的两个三角形（ ）
A．全等 B．不全等 C．不一定全等 D．以上判断都不对
3．如图1，△ABC的两边AB和AC的垂直平分线分别交BC于D、E，若边BC长为8cm，则△ADE的周长为（ ）
A．不能确定 B．8cm C．16cm D．4cm

(1) (2)
4．如图2，AB∥CD，BC∥AD，AB=CD，BE=DF，则图中全等的三角形有（ ）
A．5对 B．6对 C．3对 D．4对
5．根据已知条件，再补充一个条件，使图3中的△ABC≌△A′B′C′．
（1）AB=A′B′，AC=A′C′，_______________；（要求用SSS）
（2）AB=A′B′，AC=A′C′，_______________；（要求用SAS）
（3）AB=A′B′，BC=B′C′，_______________；（要求用SAS）
（4）AB=A′B′，∠A=∠A′，_______________．（要求用SAS）

(3) (4)
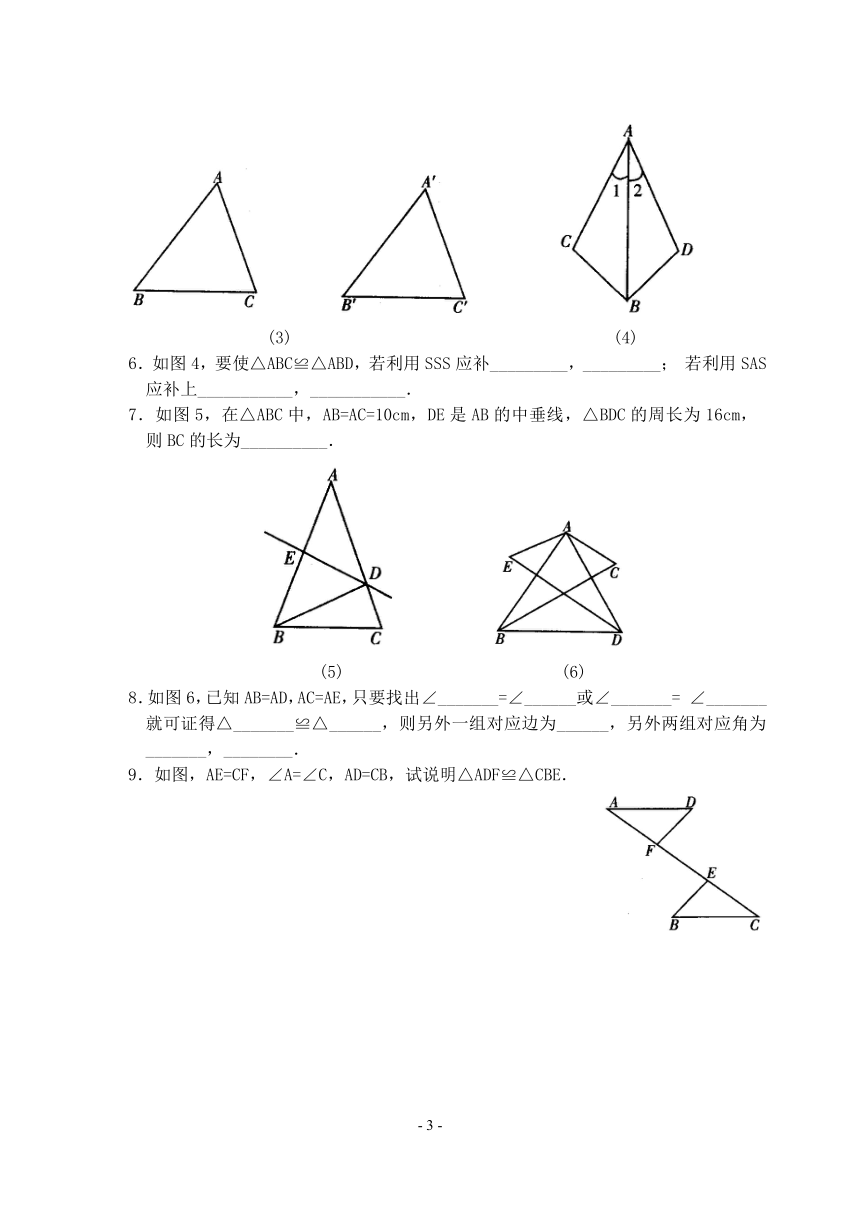
6．如图4，要使△ABC≌△ABD，若利用SSS应补_________，_________；若利用SAS应补上___________，___________．
7．如图5，在△ABC中，AB=AC=10cm，DE是AB的中垂线，△BDC的周长为16cm，则BC的长为__________．

(5) (6)
8．如图6，已知AB=AD，AC=AE，只要找出∠_______=∠______或∠_______=∠_______就可证得△_______≌△______，则另外一组对应边为______，另外两组对应角为_______，________．
9．如图，AE=CF，∠A=∠C，AD=CB，试说明△ADF≌△CBE．
10．如图，已知CE⊥AB，DF⊥AB，垂足分别为E、F，CE=DF，AB=EF．试说明：AC∥BD．
提高训练
11．如图，△ABC≌△A′B′C′．AD、A′D′为△ABC与△A′B′C′的中线，试说明AD=A′D′．
12．如图，在△ABC中，AB=5，AC=3，则BC上的中线AD的取值范围是多少？
应用拓展
13．如图，在△ABC中，D是BC的中点，DE⊥DF，延长ED至P，使ED=DP，连接FP与CP，试判断BE+CF与EF的大小关系．
14．如图，已知AB=CD=AE=BC+DE=2．∠ABC=∠AED=90°，求五边形ABCDE的面积．
答案:
1．C 2．C 3．B 4．C
5．（1）BC=B′C′ （2）∠A=∠A′ （3）∠B=∠B′ （4）AC=A′C′
6．AC=AD BC=BD AC=AD ∠1=∠2
7．6cm
8．∠CAD=∠EAB ∠CAB=∠EAD △ABC △ADE
BC与ED ∠ABC与∠ADE ∠C与∠E
9．∵AE=CF ∴AF=CE
又∵∠A=∠C AD=CB
∴△ADF≌△CBE（SAS）
10．∵CE⊥AB，DF⊥AB ∴∠CEA=∠DFB=90°
由AB=EF得AE=BF，在△ACE和△BDF中，AE=BF ∠CEA=∠DFB CE=DF 
∴△ACE≌△BDF ∴∠A=∠DBF ∴AC∥BD
11．△ABC≌△A′B′C′ ∴AB=A′B′ ∠B=∠B′ BC=B′C′
又∵AD为△ABC的中线，A′D′为△A′B′C′的中线
∴BD=BC B′D′=B′C′
∴BD=B′D′
∴△ABD≌△A′B′D′（SAS）
∴AD=A′D′
12．延长AD至E，使AD=DE，并连接BE，则△ACD≌△EBD（SAS）
∴AC=BE，在△AEB中，AB+BE>2AD>AB-BE 即4>AD>1
13．由△BDE≌△CDP，得BE=CP，
由△EDF≌△PDF，得EF=FP，在△CFP中，CP+CF=BE+CF>FP=EF
14．延长DE至F，使EF=BC，连AC、AD、AF可证明△ABC≌△AEF，△ACD≌△AFD，
∴S五边形ABCDE=2S△ADF=4