1.6 尺规作图

1．6 作三角形
【知识提要】
1．会用直尺和圆规作角平分线和线段的垂直平分线．
2．会用直尺和圆规作一个角等于已知角．
3．会用直尺和圆规作三角形：已知三边作三角形，已知两边及其夹角作三角形；已知两角及其一边作三角形．
【学法指导】
用圆规和直尺画三角形是尺规作图的重要基础，在日常生活和生产实际中也有较多应用，已知两边及其夹角；已知两角及其一边；已知三边能且只能作一个三角形，这里的“一个三角形”的含义是：当三角形的大小、形状完全相同时无论位置如何，都视作同一个三角形．
范例积累
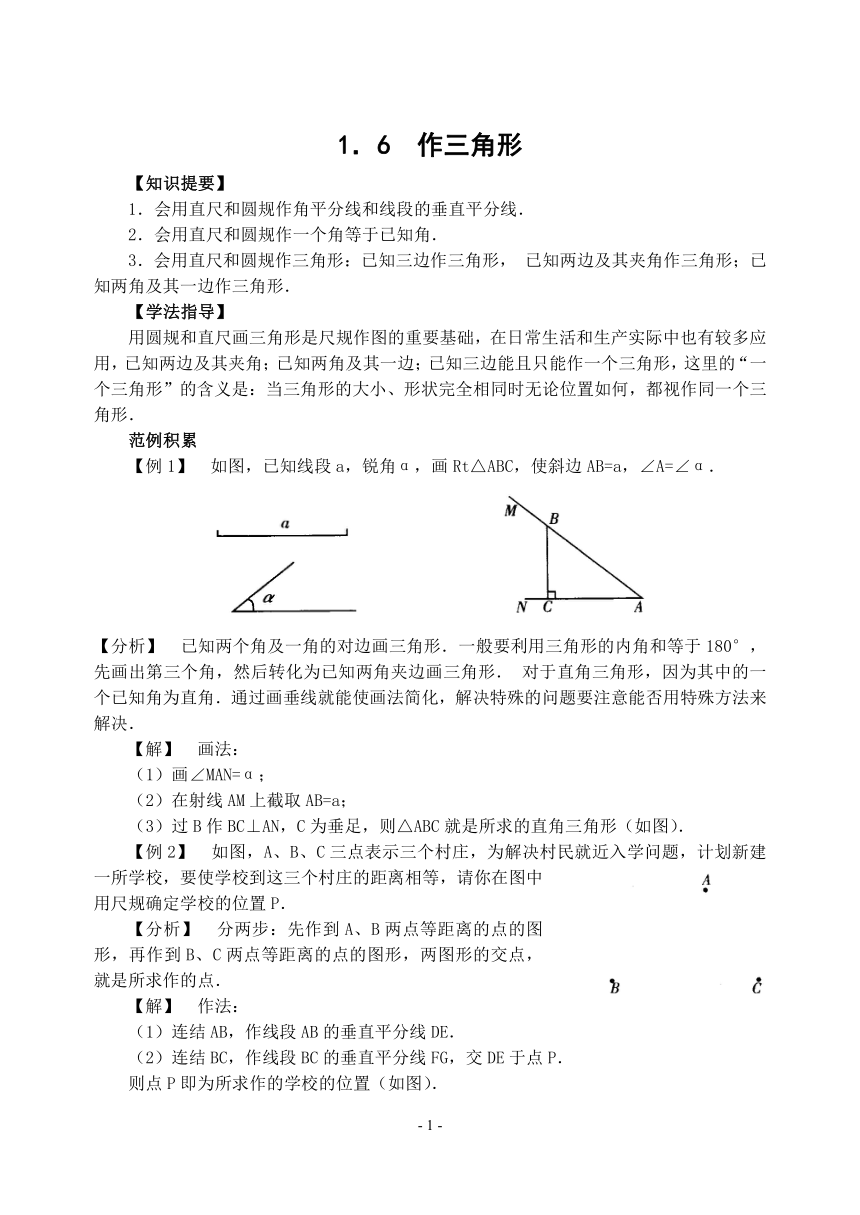
【例1】 如图，已知线段a，锐角α，画Rt△ABC，使斜边AB=a，∠A=∠α．

【分析】 已知两个角及一角的对边画三角形．一般要利用三角形的内角和等于180°，先画出第三个角，然后转化为已知两角夹边画三角形．对于直角三角形，因为其中的一个已知角为直角．通过画垂线就能使画法简化，解决特殊的问题要注意能否用特殊方法来解决．
【解】 画法：
（1）画∠MAN=α；
（2）在射线AM上截取AB=a；
（3）过B作BC⊥AN，C为垂足，则△ABC就是所求的直角三角形（如图）．
【例2】 如图，A、B、C三点表示三个村庄，为解决村民就近入学问题，计划新建一所学校，要使学校到这三个村庄的距离相等，请你在图中用尺规确定学校的位置P．
【分析】 分两步：先作到A、B两点等距离的点的图形，再作到B、C两点等距离的点的图形，两图形的交点，就是所求作的点．
【解】 作法：
（1）连结AB，作线段AB的垂直平分线DE．
（2）连结BC，作线段BC的垂直平分线FG，交DE于点P．
则点P即为所求作的学校的位置（如图）．
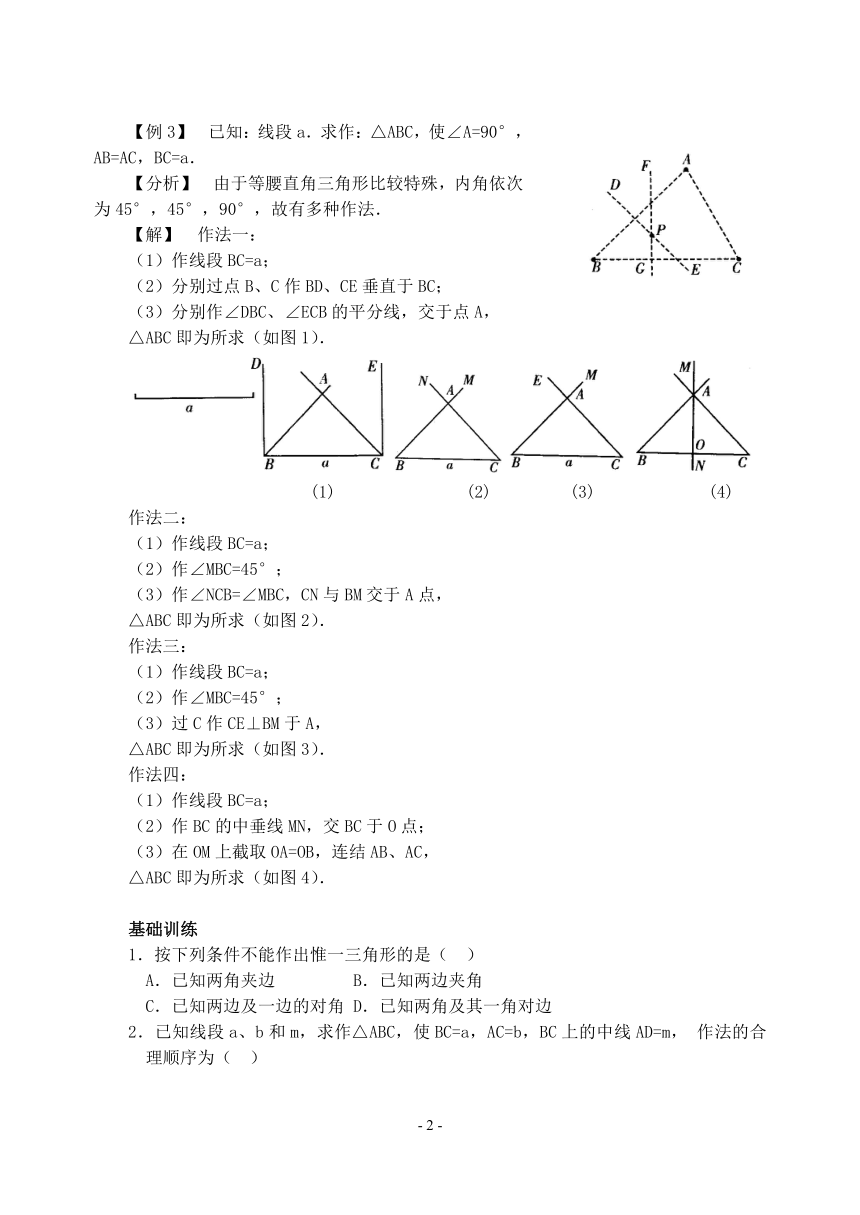
【例3】 已知：线段a．求作：△ABC，使∠A=90°，AB=AC，BC=a．
【分析】 由于等腰直角三角形比较特殊，内角依次为45°，45°，90°，故有多种作法．
【解】 作法一：
（1）作线段BC=a；
（2）分别过点B、C作BD、CE垂直于BC；
（3）分别作∠DBC、∠ECB的平分线，交于点A，
△ABC即为所求（如图1）．
(1) (2) (3) (4)
作法二：
（1）作线段BC=a；
（2）作∠MBC=45°；
（3）作∠NCB=∠MBC，CN与BM交于A点，
△ABC即为所求（如图2）．
作法三：
（1）作线段BC=a；
（2）作∠MBC=45°；
（3）过C作CE⊥BM于A，
△ABC即为所求（如图3）．
作法四：
（1）作线段BC=a；
（2）作BC的中垂线MN，交BC于O点；
（3）在OM上截取OA=OB，连结AB、AC，
△ABC即为所求（如图4）．
基础训练
1．按下列条件不能作出惟一三角形的是（ ）
A．已知两角夹边 B．已知两边夹角
C．已知两边及一边的对角 D．已知两角及其一角对边
2．已知线段a、b和m，求作△ABC，使BC=a，AC=b，BC上的中线AD=m，作法的合理顺序为（ ）
①延长CD到B，使BD=CD；②连结AB；③作△ADC，使DC=a，AC=b，AD=m
A．③①② B．①②③ C．②③① D．③②①
3．已知三边作三角形，用到的基本作图是（ ）
A．作一个角等于已知角 B．平分一个已知角
C．在射线上截取一线段等于已知线段 D．作一条直线的垂线
4．已知线段a、b（a>2b），以a、b为边作等腰三角形，则（ ）
A．只能作以a为底边的等腰三角形 B．只能作以b为底边的等腰三角形
C．可以作分别以a、b为底边的等腰三角形 D．不能作符合条件的等腰三角形
5．看图填空：
（1）过点________和点_______作直线；
（2）延长线段________到_________，且使________=_________．
（3）过点_________作直线_______的垂线；
（4）作射线_______，使_____平分∠________．
6．根据下列要求，判断是否一定能作出图形：
①过已知三点作一条直线；②作直线OP的垂直平分线MN；
③过点A作线段MN的垂线AB；④过点A作线段MN的垂直平分线；
⑤过已知线段外一点作其平行线； ⑥作△ABC的边BC的高AD且平分BC；
⑦以O为圆心作弧；⑧以O为圆心任意长为半径作弧．
能作出图形的是_________，不能作出图形的是__________．
7．如图，已知△ABC，求作△A1B1C1，使△ABC≌△A1B1C1．
8．已知：线段a、m、h（m>h），求作：
一个三角形△ABC，使BC=a，BC边上的高线AH=h，中线AM=m．
提高训练
9．已知两角α与β和其中一角的对边a．求作：
三角形ABC，使∠B=∠α，∠A=β，BC=a．
10．如图，在△ABC中找一点P，使P到AB和AC的距离相等，并且到B、C两点的距离也相等．
应用拓展
11．已知线段a和c（a答案:
1．C 2．A 3．C 4．B
5．（1）A B （2）AC B BC AC （3）M b （4）OC OC AOB
6．③⑤⑧ ①②④⑥⑦ 7～11．略。