1.1认识三角形1

赤溪中心学校电子备课纸
主备老师：凌媛 二次备课老师： 学 科： 数学
教学内容 1.1认识三角形 总课时数2 第（ 1 ）课时
设计人 凌媛 备课日期 2013 年 9月 1 日
教学目标 进一步认识三角形的概念会用符号、字母表示三角形了解三角形的按角分类理解“三角形任何两边的和大于第三边”
教学重点 三角形任何两边的和大于第三边
难点 判断三条线段能否组成三角形
课前准备
教学过程 二次备课
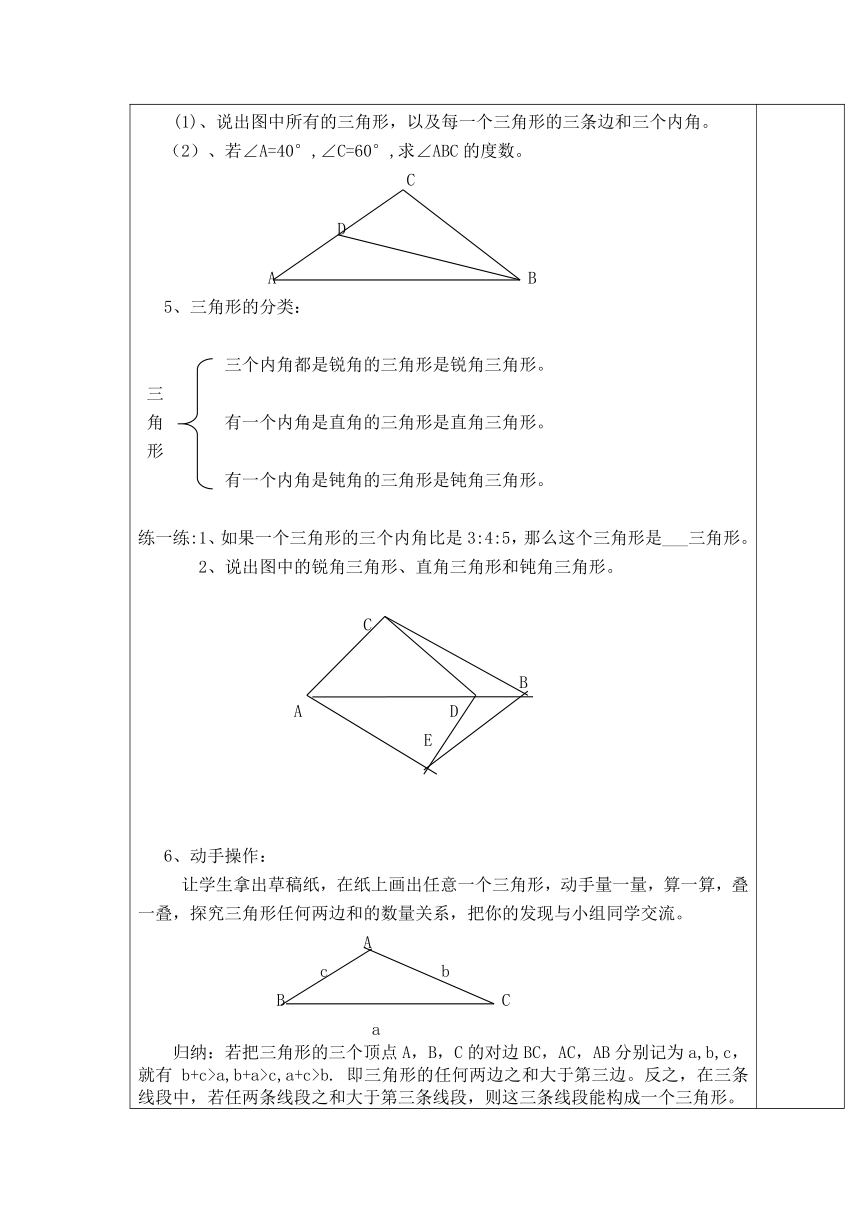
巧设情境 生活中的三角形（图片） A你能举出在生活中看到的三角形的例子吗？那么，怎样的图形叫做三角形呢？探究新知1、三角形的定义： B C由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。 2、三角形的表示方法：“三角形”用符号“△”表示，如图，顶点是A，B，C的三角形记做“△ABC”， 读作“三角形ABC”。三角形的三要素：角：∠A，∠B，∠C是在三角形的内部，由相邻两边组成的角，称为三角形的内角，简称三角形的角。顶点：三角形中有三个顶点，顶点A，顶点B，顶点C。边：AB、BC和AC是三角形的三条边。三角形的内角性质：三角形三个内角的和等于180°. 做一做:(1)、说出图中所有的三角形，以及每一个三角形的三条边和三个内角。 （2）、若∠A=40°,∠C=60°,求∠ABC的度数。C D A B 5、三角形的分类： 三个内角都是锐角的三角形是锐角三角形。三角 有一个内角是直角的三角形是直角三角形。形 有一个内角是钝角的三角形是钝角三角形。 练一练:1、如果一个三角形的三个内角比是3:4:5，那么这个三角形是___三角形。2、说出图中的锐角三角形、直角三角形和钝角三角形。 CBA DE 6、动手操作： 让学生拿出草稿纸，在纸上画出任意一个三角形，动手量一量，算一算，叠一叠，探究三角形任何两边和的数量关系，把你的发现与小组同学交流。Ac bB Ca归纳：若把三角形的三个顶点A，B，C的对边BC，AC，AB分别记为a,b,c，就有 b+c>a,b+a>c,a+c>b. 即三角形的任何两边之和大于第三边。反之，在三条线段中，若任两条线段之和大于第三条线段，则这三条线段能构成一个三角形。 思考：为什么有人喜欢斜穿人行横道？(两点之间线段最短)CB A 练一练：如图，在△ABC中，D是AB上一点，且AD=AC，连结CD。在下面各空格中填入“>”或“<”,并说明理由。 A（1）AB______AC+BC (2)AD_____CD D B C——————————————7、想一想：长度为6cm, 4cm, 3cm三条线段能否组成三角形？你有更好的判断方法吗？(1)找出最长线段。(2)比较大小：较短两边之和与最长线段的大小(3)判断能否组成三角形。8、例1：判断下列各组线段中，哪些能组成三角形，哪些不能组成三角形，并说明理由。(1)a=2.5cm, b=3cm, c=5cm (2)e=6cm, f=6cm, g=12cm.练一练: 由下列长度的三条线段能组成三角形吗 为什么 (1) a=1cm, b=2cm, c=3.5cm（2）a=4 cm, b=5cm, c=9cm;（3） a=7cm, b=7cm, c=4cm（4）a+1, a+1, 2a(a>0)拓展：刚刚我们探究了三角形任意两边之和的问题，下面请同学们自己画一画，量一量，算一算，探究三角形任何两边的差的问题。结论：三角形任何两边之差小于第三边。问题：你是如何理解三角形任何两边的和大于第三边，三角形任何两边的差小于第三边的？ （ ︳两边之差︳ 第三边 两边之和 ）填空：若三角形的两边长分别为a和b,(设ab)则第三边c的范围是____。 若在△ABC中，AB=9，BC=4，则AC的取值范围是__________.巩固练习1、如图，图中共有___个三角形，分别是_____________,以AC为一边的三角形分别是_________,∠BFE是______的内角，以∠A为内角的三角形有________.AE DB F C2、三角形的两边长分别为18cm和8cm，第三边与其中一边长相等，则第三边长为_____cm,若周长为偶数，则第三边的长度为_______. 3、在△ABC中，AB=7，BC=3，并且AC为奇数，那么△ABC的周长为________。4、现有木棒4根,长度分别为12, 8, 5, 6, 选其中3根组成三角形,则能组成三角形的个数是( ) A.1 B.2 C.3 D.4 5、在四边形ABCD中，∠B=90°.问：BC教学反思