第6章 图形的初步知识【挑战满分】2022-2023学年七年级数学上册 精选精练(浙教版)
文档属性
| 名称 | 第6章 图形的初步知识【挑战满分】2022-2023学年七年级数学上册 精选精练(浙教版) |  | |
| 格式 | doc | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 09:07:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 图形的初步知识
一、单选题
1.下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
2.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
3.若,则的补角是( )
A. B. C. D.
4.将如图所示的图形剪去两个小正方形,使余下的部分图形恰好能折成一个正方体,应剪去的两个小正方形可以是( )
A.②③ B.①⑥ C.①⑦ D.②⑥
5.下列四个图中,是三棱锥的表面展开图的是( )
A. B. C. D.
6.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4 B.3 C.2 D.1
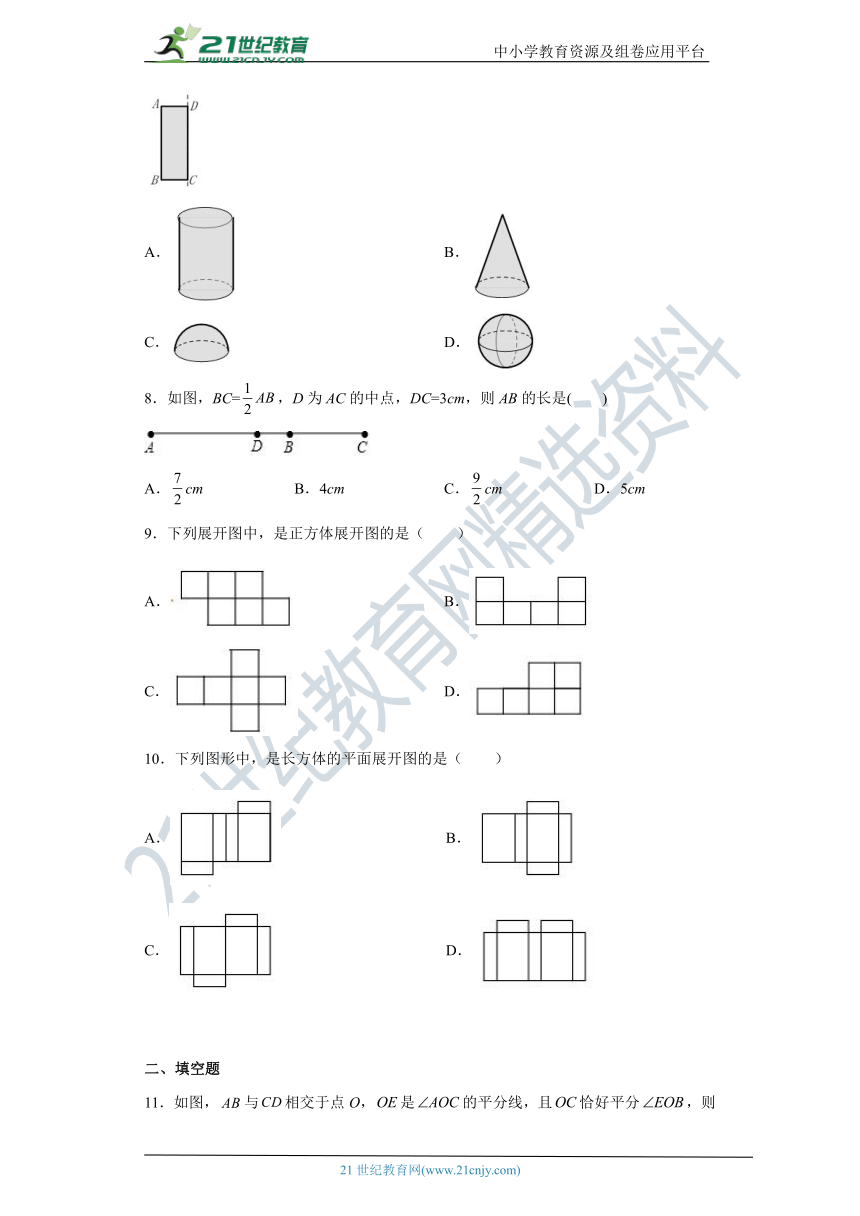
7.如图,将矩形纸片绕边所在的直线旋转一周,得到的立体图形是( )
A. B.
C. D.
8.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
9.下列展开图中,是正方体展开图的是( )
A. B.
C. D.
10.下列图形中,是长方体的平面展开图的是( )
A. B.
C. D.
二、填空题
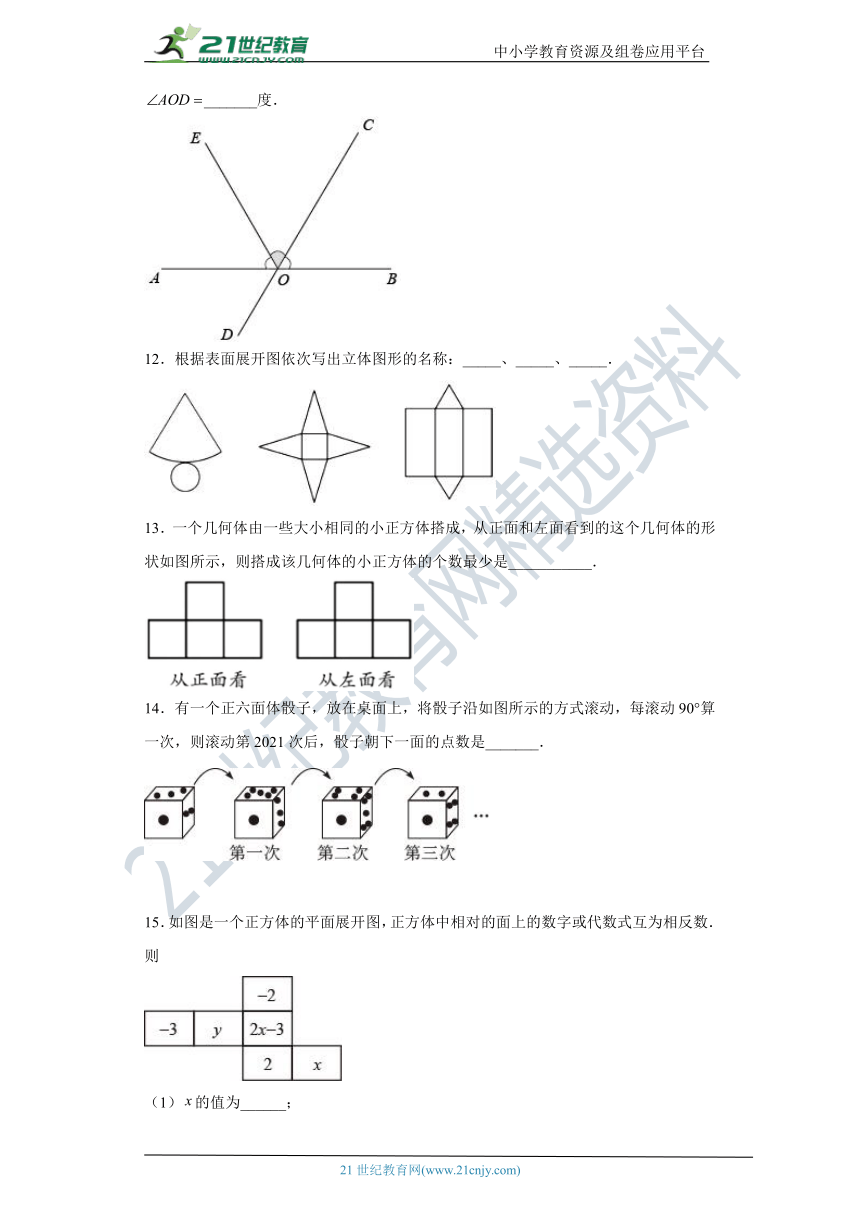
11.如图,与相交于点O,是的平分线,且恰好平分,则_______度.
12.根据表面展开图依次写出立体图形的名称:_____、_____、_____.
13.一个几何体由一些大小相同的小正方体搭成,从正面和左面看到的这个几何体的形状如图所示,则搭成该几何体的小正方体的个数最少是___________.
14.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是_______.
15.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
(1)的值为______;
(2)的值为______.
16.如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.
17.将一根长4m的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60dm2,这根木料的体积是______m3.
三、解答题
18.如图,已知线段a,b,其中a>b
(1)用圆规和直尺作线段AB,使AB=2a+b(不写作法,保留作图痕迹);
(2)如图2,点A、B、C在同一条直线上,AB=6cm,BC=2cm,若点D是线段AC的中点,求线段BD的长.
19.按照下列要求完成画图及相应的问题解答.
(1)画直线;
(2)画;
(3)画线段;
(4)过点画直线的垂线,垂足为点;
(5)点到直线的距离是线段 的长度﹒
20.如图,点在线段的延长线上,,是的中点,若,求的长.
21.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
参考答案:
1.C
【分析】根据正方体的展开图的特征,11种不同情况进行判断即可.
【详解】解:根据正方体的展开图的特征,只有第2个图不是正方体的展开图,故四个图中有3个图是正方体的展开图.
故选:C.
【点睛】考查正方体的展开图的特征,“一线不过四,田凹应弃之”应用比较广泛简洁.
2.C
【分析】根据棱柱有两个底面求出侧面数,即可选择.
【详解】棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
3.C
【分析】根据补角的定义,即若两个角的和等于 ,就称这两个角互补,即可解答.
【详解】解:∵,
∴的补角等于 ,
故选:C
【点睛】本题主要考查了补角的定义,解题的关键是熟练掌握若两个角的和等于 ,就称这两个角互补.
4.A
【分析】利用正方体及其表面展开图的特点解题.
【详解】A. 剪去②③后,恰好能折成一个正方体,符合题意;
B. 剪去①⑥后,不能折成一个正方体,不符合题意;
C. 剪去 ①⑦后,不能折成一个正方体,不符合题意;
D. 剪去 ②⑥后,不能折成一个正方体,不符合题意.
故选:A
【点睛】本题考查了正方体的展开图及学生的空间想象能力,正方体展开图规律:十一种类看仔细,中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃.
5.B
【分析】根据三棱锥是由四个三角形组成,即可求解
【详解】解:A是四棱柱,故该选项不正确,不符合题意;
B是三棱锥,故该选项正确,符合题意;
C是四棱锥,故该选项不正确,不符合题意;
D是三棱柱,故该选项不正确,不符合题意;
故选B.
【点睛】.本题考查了三棱锥的侧面展开图,解题的关键是掌握三棱锥是由四个三角形组成.
6.C
【分析】由AB=10cm,BC=4cm.于是得到AC=AB+BC=14cm,根据线段中点的定义由D是AC的中点,得到AD,根据线段的和差得到MD=AD﹣AM,于是得到结论.
【详解】解:∵AB=10cm,BC=4cm,
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
【点睛】此题主要考查了两点之间的距离,线段的和差、线段的中点的定义,利用线段差及中点性质是解题的关键.
7.A
【分析】根据矩形绕一边旋转一周得到圆柱体示来解答.
【详解】解:矩形纸片绕边所在的直线旋转一周,得到的立体图形是圆柱体.
故选:A.
【点睛】本题考查了点、线、面、体,熟练掌握“面动成体”得到的几何体的形状是解题的关键.
8.B
【分析】先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
9.C
【分析】根据正方体的表面展开图共有11种情况,A,D是“田”型,对折不能折成正方体,B是“凹”型,不能围成正方体,由此可进行选择.
【详解】解:根据正方体展开图特点可得C答案可以围成正方体,
故选:C.
【点睛】此题考查了正方体的平面展开图.关键是掌握正方体展开图特点.
10.B
【分析】根据长方体有六个面,展开后长方体相对的两个面不可能相邻进行判断.
【详解】A.中间两个细长方形相邻,错误;
B.各个相对的面没有相邻,正确;
C.中间两个大长方形相邻,错误;
D.图中有七个面,错误;
故选 B.
【点睛】本题考查几何体的展开,关键在于理解长方体有六个面,展开后长方体相对的两个面不可能相邻.
11.60
【分析】先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
【点睛】本题考查了角平分线的定义、平角的定义、对顶角相等,熟练掌握角平分线的定义是解题关键.
12. 圆锥 四棱锥 三棱柱
【分析】根据表面展开图的形状判断即可.
【详解】解:圆锥的表面展开图是一个扇形和圆,四棱锥的表面展开是一个四边形和四个三角形,三棱柱的表面展开是三个长方形和两个三角形.
故答案为:圆锥,四棱锥,三棱柱.
【点睛】本题考查立体图形的表面展开,熟悉各几何体表面展开的形状是求解本题的关键.
13.4
【分析】由主视图和左视图确定俯视图的形状,再判断最少的正方体的个数.
【详解】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共3行,
所以小正方体的个数最少的几何体为:
第一列第一行1个小正方体,第二列第二行2个小正方体,第三列第三行1个小正方体,其余位置没有小正方体.
即组成这个几何体的小正方体的个数最少为:1+2+1=4个.
故答案为:4.
【点睛】本题考查了学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
14.2
【分析】观察图形知道第一次点数五和点二数相对,第二次点数四和点数三相对,第三次点数二和点数五相对,第四次点数三和点数四相对,第五次点数五和点二数相对,且四次一循环,从而确定答案.
【详解】观察图形知道:
第一次点数五和点二数相对,
第二次点数四和点数三相对,
第三次点数二和点数五相对,
第四次点数三和点数四相对,
第五次点数五和点二数相对,
且四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故答案为:2.
【点睛】本题考查了正方体相对两个面上的文字及图形类的变化规律问题,解题的关键是发现规律.
15. 3 12
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数列式,即可求出x、y的值,
(2)把x,y的值代入代数式进行计算即可得解.
【详解】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”与“2x 3”是相对面,“y”与“x”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x 3+(-3)=0,x+y=0,
解得x=3,y=-3,
故答案是:3;
(2)当x=3,y=-3时,=,
故答案是:12.
【点睛】本题主要考查了正方体相对两个面上的文字,二元一次方程组以及代数式求值,注意正方体的空间图形,从相对面入手,分析及解答问题.
16.月
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:由正方体的展开图特点可得:“神”字对面的字是“月”.
故答案为:月.
【点睛】此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.
17.1.2
【分析】将一根长4m的圆柱体木料锯成2段,增加两个底面,又知表面积增加60dm2,由此求出这根木料的底面积,根据圆柱的体积公式即可计算.
【详解】解:60dm2=0.6m2
0.6÷2=0.3(m2)
0.3×4=1.2(m3),
故这根木料的体积是1.2m3.
故答案为:1.2.
【点睛】本题考查了计算圆柱的体积.解题的关键是掌握圆柱的体积公式.
18.(1)见解析;(2)DB=2cm.
【分析】(1)作射线AP,在射线AP上依次截取AM=MN=a,NB=b,据此可得;
(2)先求出线段AC的长,再由中点得出DC的长,依据DB=DC﹣BC可得.
【详解】解:(1)如图所示,线段AB即为所求.
(2)∵AB=6cm,BC=2cm,
∴AC=AB+BC=8cm,
∵点D是线段AC的中点,
∴DC=AC=4cm,
∴DB=DC﹣BC=2cm.
【点睛】考查作图﹣复杂作图,解题的关键是掌握作一线段等于已知线段的尺规作图和线段的和差计算.
19.(1)见解析;(2)见解析;(3)见解析;(4)见解析;(5)CD
【分析】(1)画直线AB即可;
(2)画∠BAC即可;
(3)画线段BC即可;
(4)过C点画直线AB的垂线,交直线AB于点D即可;
(5)根据点到直线的距离即可得点C到直线AB的距离.
【详解】解:
如图所示:
(1)直线AB即为所求作的图形;
(2)∠BAC即为所求作的图形;
(3)线段BC即为所求作的图形;
(4)过C点画直线AB的垂线,交直线AB于点D,CD即为所求作的图形;
(5)点C到直线AB的距离为线段CD的长.
【点睛】本题考查了作图,作直线、射线、线段、垂线、点到直线的距离,解决本题的关键是根据语句准确画出图形.
20.7.5
【分析】根据AC与AB的关系,可得AC的长,根据线段的中点分线段相等,可得AD与AC的关系,根据线段的和差,可得答案.
【详解】解:,,
∴AC=3×15=45.
又是的中点,
,
【点睛】本题考查了两点间的距离,线段的中点,解题的关键是根据AC与AB关系,先求出AC的长,再根据线段的中点分线段相等求得答案.
21.(1)面会在上面;(2)面会在上面;(3)面会在前面
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
试卷第1页,共3页
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第六章 图形的初步知识
一、单选题
1.下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
2.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
3.若,则的补角是( )
A. B. C. D.
4.将如图所示的图形剪去两个小正方形,使余下的部分图形恰好能折成一个正方体,应剪去的两个小正方形可以是( )
A.②③ B.①⑥ C.①⑦ D.②⑥
5.下列四个图中,是三棱锥的表面展开图的是( )
A. B. C. D.
6.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4 B.3 C.2 D.1
7.如图,将矩形纸片绕边所在的直线旋转一周,得到的立体图形是( )
A. B.
C. D.
8.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
9.下列展开图中,是正方体展开图的是( )
A. B.
C. D.
10.下列图形中,是长方体的平面展开图的是( )
A. B.
C. D.
二、填空题
11.如图,与相交于点O,是的平分线,且恰好平分,则_______度.
12.根据表面展开图依次写出立体图形的名称:_____、_____、_____.
13.一个几何体由一些大小相同的小正方体搭成,从正面和左面看到的这个几何体的形状如图所示,则搭成该几何体的小正方体的个数最少是___________.
14.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是_______.
15.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
(1)的值为______;
(2)的值为______.
16.如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.
17.将一根长4m的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60dm2,这根木料的体积是______m3.
三、解答题
18.如图,已知线段a,b,其中a>b
(1)用圆规和直尺作线段AB,使AB=2a+b(不写作法,保留作图痕迹);
(2)如图2,点A、B、C在同一条直线上,AB=6cm,BC=2cm,若点D是线段AC的中点,求线段BD的长.
19.按照下列要求完成画图及相应的问题解答.
(1)画直线;
(2)画;
(3)画线段;
(4)过点画直线的垂线,垂足为点;
(5)点到直线的距离是线段 的长度﹒
20.如图,点在线段的延长线上,,是的中点,若,求的长.
21.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
参考答案:
1.C
【分析】根据正方体的展开图的特征,11种不同情况进行判断即可.
【详解】解:根据正方体的展开图的特征,只有第2个图不是正方体的展开图,故四个图中有3个图是正方体的展开图.
故选:C.
【点睛】考查正方体的展开图的特征,“一线不过四,田凹应弃之”应用比较广泛简洁.
2.C
【分析】根据棱柱有两个底面求出侧面数,即可选择.
【详解】棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
3.C
【分析】根据补角的定义,即若两个角的和等于 ,就称这两个角互补,即可解答.
【详解】解:∵,
∴的补角等于 ,
故选:C
【点睛】本题主要考查了补角的定义,解题的关键是熟练掌握若两个角的和等于 ,就称这两个角互补.
4.A
【分析】利用正方体及其表面展开图的特点解题.
【详解】A. 剪去②③后,恰好能折成一个正方体,符合题意;
B. 剪去①⑥后,不能折成一个正方体,不符合题意;
C. 剪去 ①⑦后,不能折成一个正方体,不符合题意;
D. 剪去 ②⑥后,不能折成一个正方体,不符合题意.
故选:A
【点睛】本题考查了正方体的展开图及学生的空间想象能力,正方体展开图规律:十一种类看仔细,中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃.
5.B
【分析】根据三棱锥是由四个三角形组成,即可求解
【详解】解:A是四棱柱,故该选项不正确,不符合题意;
B是三棱锥,故该选项正确,符合题意;
C是四棱锥,故该选项不正确,不符合题意;
D是三棱柱,故该选项不正确,不符合题意;
故选B.
【点睛】.本题考查了三棱锥的侧面展开图,解题的关键是掌握三棱锥是由四个三角形组成.
6.C
【分析】由AB=10cm,BC=4cm.于是得到AC=AB+BC=14cm,根据线段中点的定义由D是AC的中点,得到AD,根据线段的和差得到MD=AD﹣AM,于是得到结论.
【详解】解:∵AB=10cm,BC=4cm,
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
【点睛】此题主要考查了两点之间的距离,线段的和差、线段的中点的定义,利用线段差及中点性质是解题的关键.
7.A
【分析】根据矩形绕一边旋转一周得到圆柱体示来解答.
【详解】解:矩形纸片绕边所在的直线旋转一周,得到的立体图形是圆柱体.
故选:A.
【点睛】本题考查了点、线、面、体,熟练掌握“面动成体”得到的几何体的形状是解题的关键.
8.B
【分析】先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
9.C
【分析】根据正方体的表面展开图共有11种情况,A,D是“田”型,对折不能折成正方体,B是“凹”型,不能围成正方体,由此可进行选择.
【详解】解:根据正方体展开图特点可得C答案可以围成正方体,
故选:C.
【点睛】此题考查了正方体的平面展开图.关键是掌握正方体展开图特点.
10.B
【分析】根据长方体有六个面,展开后长方体相对的两个面不可能相邻进行判断.
【详解】A.中间两个细长方形相邻,错误;
B.各个相对的面没有相邻,正确;
C.中间两个大长方形相邻,错误;
D.图中有七个面,错误;
故选 B.
【点睛】本题考查几何体的展开,关键在于理解长方体有六个面,展开后长方体相对的两个面不可能相邻.
11.60
【分析】先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
【点睛】本题考查了角平分线的定义、平角的定义、对顶角相等,熟练掌握角平分线的定义是解题关键.
12. 圆锥 四棱锥 三棱柱
【分析】根据表面展开图的形状判断即可.
【详解】解:圆锥的表面展开图是一个扇形和圆,四棱锥的表面展开是一个四边形和四个三角形,三棱柱的表面展开是三个长方形和两个三角形.
故答案为:圆锥,四棱锥,三棱柱.
【点睛】本题考查立体图形的表面展开,熟悉各几何体表面展开的形状是求解本题的关键.
13.4
【分析】由主视图和左视图确定俯视图的形状,再判断最少的正方体的个数.
【详解】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共3行,
所以小正方体的个数最少的几何体为:
第一列第一行1个小正方体,第二列第二行2个小正方体,第三列第三行1个小正方体,其余位置没有小正方体.
即组成这个几何体的小正方体的个数最少为:1+2+1=4个.
故答案为:4.
【点睛】本题考查了学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
14.2
【分析】观察图形知道第一次点数五和点二数相对,第二次点数四和点数三相对,第三次点数二和点数五相对,第四次点数三和点数四相对,第五次点数五和点二数相对,且四次一循环,从而确定答案.
【详解】观察图形知道:
第一次点数五和点二数相对,
第二次点数四和点数三相对,
第三次点数二和点数五相对,
第四次点数三和点数四相对,
第五次点数五和点二数相对,
且四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故答案为:2.
【点睛】本题考查了正方体相对两个面上的文字及图形类的变化规律问题,解题的关键是发现规律.
15. 3 12
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数列式,即可求出x、y的值,
(2)把x,y的值代入代数式进行计算即可得解.
【详解】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”与“2x 3”是相对面,“y”与“x”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x 3+(-3)=0,x+y=0,
解得x=3,y=-3,
故答案是:3;
(2)当x=3,y=-3时,=,
故答案是:12.
【点睛】本题主要考查了正方体相对两个面上的文字,二元一次方程组以及代数式求值,注意正方体的空间图形,从相对面入手,分析及解答问题.
16.月
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:由正方体的展开图特点可得:“神”字对面的字是“月”.
故答案为:月.
【点睛】此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.
17.1.2
【分析】将一根长4m的圆柱体木料锯成2段,增加两个底面,又知表面积增加60dm2,由此求出这根木料的底面积,根据圆柱的体积公式即可计算.
【详解】解:60dm2=0.6m2
0.6÷2=0.3(m2)
0.3×4=1.2(m3),
故这根木料的体积是1.2m3.
故答案为:1.2.
【点睛】本题考查了计算圆柱的体积.解题的关键是掌握圆柱的体积公式.
18.(1)见解析;(2)DB=2cm.
【分析】(1)作射线AP,在射线AP上依次截取AM=MN=a,NB=b,据此可得;
(2)先求出线段AC的长,再由中点得出DC的长,依据DB=DC﹣BC可得.
【详解】解:(1)如图所示,线段AB即为所求.
(2)∵AB=6cm,BC=2cm,
∴AC=AB+BC=8cm,
∵点D是线段AC的中点,
∴DC=AC=4cm,
∴DB=DC﹣BC=2cm.
【点睛】考查作图﹣复杂作图,解题的关键是掌握作一线段等于已知线段的尺规作图和线段的和差计算.
19.(1)见解析;(2)见解析;(3)见解析;(4)见解析;(5)CD
【分析】(1)画直线AB即可;
(2)画∠BAC即可;
(3)画线段BC即可;
(4)过C点画直线AB的垂线,交直线AB于点D即可;
(5)根据点到直线的距离即可得点C到直线AB的距离.
【详解】解:
如图所示:
(1)直线AB即为所求作的图形;
(2)∠BAC即为所求作的图形;
(3)线段BC即为所求作的图形;
(4)过C点画直线AB的垂线,交直线AB于点D,CD即为所求作的图形;
(5)点C到直线AB的距离为线段CD的长.
【点睛】本题考查了作图,作直线、射线、线段、垂线、点到直线的距离,解决本题的关键是根据语句准确画出图形.
20.7.5
【分析】根据AC与AB的关系,可得AC的长,根据线段的中点分线段相等,可得AD与AC的关系,根据线段的和差,可得答案.
【详解】解:,,
∴AC=3×15=45.
又是的中点,
,
【点睛】本题考查了两点间的距离,线段的中点,解题的关键是根据AC与AB关系,先求出AC的长,再根据线段的中点分线段相等求得答案.
21.(1)面会在上面;(2)面会在上面;(3)面会在前面
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
试卷第1页,共3页
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
