第2章 简单事件的概率【挑战满分】2022-2023学年九年级数学上册 精选精练(浙教版)
文档属性
| 名称 | 第2章 简单事件的概率【挑战满分】2022-2023学年九年级数学上册 精选精练(浙教版) |

|
|
| 格式 | doc | ||
| 文件大小 | 823.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第2章 简单事件的概率
一、单选题
1.若气象部门预报明天下雨的概率是70%,下列说法正确的是( )
A.明天下雨的可能性比较大
B.明天一定不会下雨
C.明天一定会下雨
D.明天下雨的可能性比较小
2.如图,两个转盘分别自由转动一次(当指针恰好指在分界线上时重转),当停止转动时,两个转盘的指针都指向3的概率为( )
A. B. C. D.
3.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有个,若随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则的值为( )
A.3 B.4 C.5 D.6
4.下列判断正确的是( )
A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B.天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨
C.“篮球队员在罚球线上投篮一次,投中”为随机事件 D.“a是实数,|a|≥0”是不可能事件
5.七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( )
A. B. C. D.
6.把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )
A. B. C. D.
7.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
8.一名运动员连续打靶次,其中次命中环,次命中环,次命中环.根据这几次打靶记录,如果再让他打靶次,那么下列说法正确的是( )
A.命中环的可能性最大 B.命中环的可能性最大
C.命中环的可能性最大 D.以上种可能性一样大
9.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是( )
实验次数 100 200 300 500 800 1000 2000
频率 0.365 0.328 0.330 0.334 0.336 0.332 0.333
A.抛一枚硬币,出现正面
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.抛一个质地均匀的正六面体骰子(六个面上分别标1,2,3,4,5,6),向上的面点数是5
D.从一个装有2个白球和1个红球的袋子中任取一球,取到红球
10.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
二、填空题
11.布袋中有红、黄、蓝三个球,它们除颜色不同以外,其他都相同,从袋中随机取出一个球后再放回袋中,这样取出球的顺序依次是“红—黄—蓝”的概率是__________.
12.一个质地均匀的骰子,其六面上分别标有数字1,2,3,4,5,6,投掷一次,朝上的面的数字小于3的概率为 ______.
13.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) 200 500 800 2000 12000
成活数(m) 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
根据表中数据,估计这种幼树移植成活率的概率为___(精确到0.1).
14.从,,,0,3这五个数中随机抽取一个数,恰好是无理数的概率是__.
15.(1)明天是晴天;(2)黑暗中从一串不同的钥匙中随意摸出一把,用它打开了门;(3)某小组有13名同学,至少有2名同学的生日在同一个月;(4)在标准大气压下,温度低于0℃时冰融化,在这些事件中属于随机事件的有__________;属于必然事件的有_______.(只填序号)
16.五张背面完全相同的卡片上分别写有、、-31、、0.101001001…(相邻两个1间依次多1个0)五个实数,如果将卡片字面朝下随意放在桌子上,任意取一张,抽到有理数的概率是______.
17.对一批口罩进行抽检,统计合格口罩的只数,得到合格口罩的频率如下:
抽取只数(只) 50 100 150 500 1000 2000 10000 50000
合格频率 0.82 0.83 0.82 0.83 0.84 0.84 0.84 0.84
估计从该批次口罩中任抽一只口罩是合格品的概率为_____.
三、解答题
18.学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 、、 三张扑克牌,乙手中有 、、 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
19.圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,随着小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从的小数部分随机取出一个数字,估计数字是6的概率为________;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
20.从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
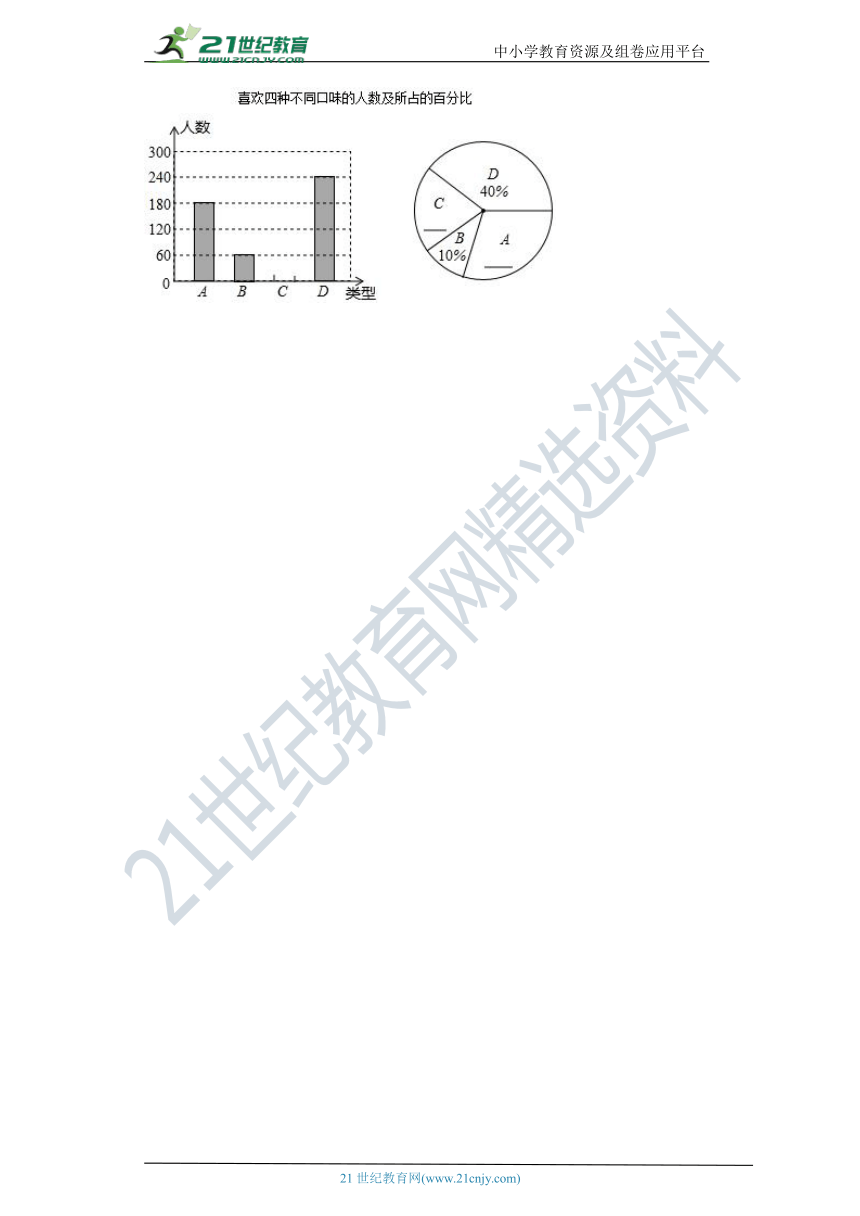
21.端午节是我国的传统节日,益民食品厂为了解市民对去年销量较好的花生粽子、水果粽子、豆沙粽子、红枣粽子(分别用A、B、C、D表示)这四种不同口味的粽子的喜爱情况,对某居民区的市民进行了抽样调查,并根据调查结果绘制了如下两幅不完整的统计图.
(1)本次参加抽样调查的居民有多少人?
(2)将两幅统计图补充完整;
(3)小明喜欢吃花生粽子和红枣粽子,妈妈为他准备了四种粽子各一个,请用“列表法”或“画树形图”的方法,求出小明同时选中花生粽子和红枣粽子的概率.
参考答案:
1.A
【分析】根据“概率”的意义进行判断即可.
【详解】解:A. 明天下雨的概率是70%,即明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项A符合题意,
B. 明天下雨的可能性比较大,与明天一定不会下雨是矛盾的,因此选项B不符合题意;
C. 明天下雨的可能性是70%,并不代表明天一定会下雨,因此选项C不符合题意;
D. 明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项D不符合题意,
故选:A.
【点睛】本题考查了概率与可能性的关系,正确理解概率的意义是解题的关键.
2.A
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与都指向3的情况数,继而求得答案.
【详解】解:列表如下:
1 2 3 4
1
2
3
4
共有16种等可能的结果,两个转盘的指针都指向3的只有1种结果,
两个转盘的指针都指向3的概率为,
故选:A.
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率所求情况数与总情况数之比.
3.A
【分析】根据题意可得,然后进行求解即可.
【详解】解:由题意得:
,
解得:,
经检验是原方程的解;
故选A.
【点睛】本题主要考查分式方程的解法及概率,熟练掌握分式方程的解法及概率是解题的关键.
4.C
【分析】直接利用概率的意义以及随机事件的定义分别分析得出答案.
【详解】A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上,错误,不符合题意;
B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨,错误,不符合题意;
C、“篮球队员在罚球线上投篮一次,投中”为随机事件,正确,符合题意;
D、“a是实数,|a|≥0”是必然事件,故此选项错误,不符合题意.
故选C.
【点睛】此题主要考查了概率的意义以及随机事件的定义,正确把握相关定义是解题关键.
5.C
【分析】首先设正方形的面积,再表示出阴影部分面积,然后可得概率.
【详解】解:设“东方模板”的面积为4,则阴影部分三角形面积为1,平行四边形面积为,
则点取自黑色部分的概率为:,
故选C.
【点睛】此题主要考查了概率,关键是表示图形的面积和阴影部分面积.
6.D
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号和大于3的情况,再利用概率公式即可求得答案.
【详解】解:根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和大于3的有6种,
∴两次摸出的小球标号的和大于3的概率是,
故选:D
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.C
【分析】利用列表法或树状图即可解决.
【详解】分别用r、b代表红色帽子、黑色帽子,用R、B、W分别代表红色围巾、黑色围巾、白色围巾,列表如下:
R B W
r rR rB rW
b bR bB bW
则所有可能的结果数为6种,其中恰好为红色帽子和红色围巾的结果数为1种,根据概率公式,恰好为红色帽子和红色围巾的概率是.
故选:C.
【点睛】本题考查了简单事件的概率,常用列表法或画树状图来求解.
8.D
【分析】根据随机事件发生的独立性,可得某次射击的结果与连续射靶100次的结果无关,所以针对某次射击,命中10环、9环、8环的可能性均等,据此解答即可.
【详解】根据随机事件发生的独立性,可得某次射击的结果与连续射靶100次的结果无关,所以针对某次射击,命中10环、9环、8环的可能性均等.如果再让他打靶次,都有可能.
故选:D.
【点睛】此题主要考查了随机事件发生的独立性问题的应用.
9.D
【分析】根据利用频率估计概率得到实验的概率在0.33左右,再分别计算出四个选项中的概率,再进行判断.
【详解】A、抛一枚硬币,出现正面的概率是,不符合题意;
B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是,不符合题意;
C、抛一个质地均匀的正六面体骰子(六个面上分别标1,2,3,4,5,6),向上的面点数是5的概率是,不符合题意;
D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率是,符合题意,
故选:D.
【点睛】此题考查频率估计概率,计算简单事件的概率,正确理解题意计算出各事件的概率是解题的关键.
10.D
【分析】根据事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,在一定条件下,可能发生也可能不发生的事件,称为随机事件进行分析即可.
【详解】A、两枚骰子向上一面的点数之和大于1,是必然事件,故此选项错误;
B、两枚骰子向上一面的点数之和等于1,是不可能事件,故此选项错误;
C、两枚骰子向上一面的点数之和大于12,是不可能事件,故此选项错误;
D、两枚骰子向上一面的点数之和等于12,是随机事件,故此选项正确;
故选:D.
【点睛】此题主要考查了随机事件的判断,关键是掌握随机事件,确定性事件的定义.
11.
【分析】列举出所有情况,看球的顺序依次是“红黄蓝”的情况数占所有情况数的多少即可.
【详解】解:画出树形图:
共有27种情况,球的顺序依次是“红黄蓝”的情况数有1种,所以概率为.
故答案为:.
【点睛】考查用列树状图的方法解决概率问题;得到球的顺序依次是“红黄蓝”的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.
12.
【分析】根据概率公式直接求解即可.
【详解】共6个数字,其中小于3的数有2个
投掷一次,朝上的面的数字小于3的概率为.
故答案为:
【点睛】本题考查了简单概率公式的计算,熟悉概率公式是解题的关键.
13.0.9
【分析】由题意根据概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率进行分析即可.
【详解】解:概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率,
∴这种幼树移植成活率的概率约为0.9.
故答案为:0.9.
【点睛】本题主要考查利用频率估计概率,大量反复试验下频率稳定值即概率.注意掌握频率=所求情况数与总情况数之比.
14.##0.4
【分析】先确定无理数的个数,再除以总个数.
【详解】解:,是无理数,
(恰好是无理数).
故答案为:.
【点睛】本题主要考查了概率公式及无理数,熟练掌握概率公式及无理数的定义进行计算是解决本题的关键.
15. (1),(2) (3)
【分析】根据事件的分类判断,随机事件就是可能发生也可能不发生的事件,必然事件就是一定发生的事件,根据定义即可解决.
【详解】(1)明天是晴天,无法确定是随机事件;
(2)黑暗中从一串不同的钥匙中随意摸出一把,用它打开了门,无法确定是随机事件;
(3)某小组有13名同学,至少有2名同学的生日在同一个月,是确定事件是必然事件;
(4)在标准大气压下,温度低于0℃时冰融化,是不可能事件,在这些事件中属于随机事件的有(1),(2);属于必然事件的有(3).
故答案为(1),(2);(3).
【点睛】本题考查了必然事件、不可能事件、随机事件的概念,必然事件指在一定条件下一定发生的事件,不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,难度适中.
16.##0.4
【分析】根据题意可知有理数有-31、,共2个,根据概率公式即可求解
【详解】解:在、、-31、、0.101001001…(相邻两个1间依次多1个0)五个实数中,-31、是有理数,
∴任意取一张,抽到有理数的概率是
故答案为:
【点睛】本题考查了实数的分类,根据概率公式求概率,理解题意是解题的关键.
17.0.84
【分析】观察表格合格的频率趋近于0.84,从而由此得到口罩合格的概率即可.
【详解】解:∵随着抽样的增大,合格的频率趋近于0.84,
∴估计从该批次口罩中任抽一只口罩是合格品的概率为0.84.
故答案为:0.84.
【点睛】本题考查了用频率估计概率,解题关键是熟练运用频率估计概率解决问题.
18.(1)详见解析;(2).
【分析】(1)根据题意可以写出所有的可能性;
(2)根据(1)中的结果可以得到乙本局获胜的可能性,从而可以解答本题.
【详解】解:(1)由题意可得,每人随机取出手中的一张牌进行比较的所有情况是:
,,,,,,,,.
(2)由()知共有9种等可能的情况,学生乙获胜的情况有:,,,
所以学生乙一局比赛获胜的概率是:.
故答案为(1)见解析;(2).
【点睛】本题考查了列表法与树状图法,概率=所求情况数与总情况数之比.
19.(1);(2)见解析,
【分析】(1)这个事件中有10种等可能性,其中是6的有一种可能性,根据概率公式计算即可;
(2)画出树状图计算即可.
【详解】(1)∵这个事件中有10种等可能性,其中是6的有一种可能性,
∴数字是6的概率为,
故答案为:;
(2)解:画树状图如图所示:
∵共有12种等可能的结果,其中有一幅是祖冲之的画像有6种情况.
∴(其中有一幅是祖冲之).
【点睛】本题考查了概率公式计算,画树状图或列表法计算概率,熟练掌握概率计算公式,准确画出树状图或列表是解题的关键.
20.(1)
(2)
【分析】(1)利用例举法例举所有的等可能的情况数,再利用概率公式进行计算即可;
(2)先列表得到所有的等可能的情况数以及符合条件的情况数,再利用概率公式进行计算即可.
(1)
解:由甲一定参加比赛,再从其余3名学生中任意选取1名,共有甲、乙,甲、丙,甲、丁三种等可能,符合条件的情况数有1种,
∴甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是
(2)
列表如下:
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
所有所有的等可能的情况数有12种,符合条件的情况数有6种,
所以一定有乙的概率为:
【点睛】本题考查的是利用例举法,列表的方法求解简单随机事件的概率,概率公式的应用,掌握“例举法与列表法求解概率”是解本题的关键.
21.(1)本次参加抽样调查的居民有600人;(2)见解析;(3).
【分析】(1)用喜欢B类的人数除以它所占的百分比得到调查的总人数;
(2)先计算出喜欢C类的人数,再计算出喜欢A类的人数的百分比和喜欢C类的人数的百分比,然后补全条形统计图和扇形统计图;
(3)画树状图展示所有12种等可能的结果数,找出小明同时选中花生粽子和红枣粽子的结果数,然后根据概率公式求解.
【详解】(1)60÷10%=600,
所以本次参加抽样调查的居民有600人;
(2)喜欢C类的人数为600﹣180﹣60﹣240=120(人),
喜欢A类的人数的百分比为×100%=30%;
喜欢C类的人数的百分比为×100%=20%;
两幅统计图补充为:
(3)画树状图为:
共有12种等可能的结果数,其中小明同时选中花生粽子和红枣粽子的结果数为2,
所以小明同时选中花生粽子和红枣粽子的概率==.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
试卷第1页,共3页
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2章 简单事件的概率
一、单选题
1.若气象部门预报明天下雨的概率是70%,下列说法正确的是( )
A.明天下雨的可能性比较大
B.明天一定不会下雨
C.明天一定会下雨
D.明天下雨的可能性比较小
2.如图,两个转盘分别自由转动一次(当指针恰好指在分界线上时重转),当停止转动时,两个转盘的指针都指向3的概率为( )
A. B. C. D.
3.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有个,若随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则的值为( )
A.3 B.4 C.5 D.6
4.下列判断正确的是( )
A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B.天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨
C.“篮球队员在罚球线上投篮一次,投中”为随机事件 D.“a是实数,|a|≥0”是不可能事件
5.七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( )
A. B. C. D.
6.把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )
A. B. C. D.
7.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
8.一名运动员连续打靶次,其中次命中环,次命中环,次命中环.根据这几次打靶记录,如果再让他打靶次,那么下列说法正确的是( )
A.命中环的可能性最大 B.命中环的可能性最大
C.命中环的可能性最大 D.以上种可能性一样大
9.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是( )
实验次数 100 200 300 500 800 1000 2000
频率 0.365 0.328 0.330 0.334 0.336 0.332 0.333
A.抛一枚硬币,出现正面
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.抛一个质地均匀的正六面体骰子(六个面上分别标1,2,3,4,5,6),向上的面点数是5
D.从一个装有2个白球和1个红球的袋子中任取一球,取到红球
10.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
二、填空题
11.布袋中有红、黄、蓝三个球,它们除颜色不同以外,其他都相同,从袋中随机取出一个球后再放回袋中,这样取出球的顺序依次是“红—黄—蓝”的概率是__________.
12.一个质地均匀的骰子,其六面上分别标有数字1,2,3,4,5,6,投掷一次,朝上的面的数字小于3的概率为 ______.
13.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) 200 500 800 2000 12000
成活数(m) 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
根据表中数据,估计这种幼树移植成活率的概率为___(精确到0.1).
14.从,,,0,3这五个数中随机抽取一个数,恰好是无理数的概率是__.
15.(1)明天是晴天;(2)黑暗中从一串不同的钥匙中随意摸出一把,用它打开了门;(3)某小组有13名同学,至少有2名同学的生日在同一个月;(4)在标准大气压下,温度低于0℃时冰融化,在这些事件中属于随机事件的有__________;属于必然事件的有_______.(只填序号)
16.五张背面完全相同的卡片上分别写有、、-31、、0.101001001…(相邻两个1间依次多1个0)五个实数,如果将卡片字面朝下随意放在桌子上,任意取一张,抽到有理数的概率是______.
17.对一批口罩进行抽检,统计合格口罩的只数,得到合格口罩的频率如下:
抽取只数(只) 50 100 150 500 1000 2000 10000 50000
合格频率 0.82 0.83 0.82 0.83 0.84 0.84 0.84 0.84
估计从该批次口罩中任抽一只口罩是合格品的概率为_____.
三、解答题
18.学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 、、 三张扑克牌,乙手中有 、、 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
19.圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,随着小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从的小数部分随机取出一个数字,估计数字是6的概率为________;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
20.从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
21.端午节是我国的传统节日,益民食品厂为了解市民对去年销量较好的花生粽子、水果粽子、豆沙粽子、红枣粽子(分别用A、B、C、D表示)这四种不同口味的粽子的喜爱情况,对某居民区的市民进行了抽样调查,并根据调查结果绘制了如下两幅不完整的统计图.
(1)本次参加抽样调查的居民有多少人?
(2)将两幅统计图补充完整;
(3)小明喜欢吃花生粽子和红枣粽子,妈妈为他准备了四种粽子各一个,请用“列表法”或“画树形图”的方法,求出小明同时选中花生粽子和红枣粽子的概率.
参考答案:
1.A
【分析】根据“概率”的意义进行判断即可.
【详解】解:A. 明天下雨的概率是70%,即明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项A符合题意,
B. 明天下雨的可能性比较大,与明天一定不会下雨是矛盾的,因此选项B不符合题意;
C. 明天下雨的可能性是70%,并不代表明天一定会下雨,因此选项C不符合题意;
D. 明天下雨的可能性是70%,也就是说明天下雨的可能性比较大,因此选项D不符合题意,
故选:A.
【点睛】本题考查了概率与可能性的关系,正确理解概率的意义是解题的关键.
2.A
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与都指向3的情况数,继而求得答案.
【详解】解:列表如下:
1 2 3 4
1
2
3
4
共有16种等可能的结果,两个转盘的指针都指向3的只有1种结果,
两个转盘的指针都指向3的概率为,
故选:A.
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率所求情况数与总情况数之比.
3.A
【分析】根据题意可得,然后进行求解即可.
【详解】解:由题意得:
,
解得:,
经检验是原方程的解;
故选A.
【点睛】本题主要考查分式方程的解法及概率,熟练掌握分式方程的解法及概率是解题的关键.
4.C
【分析】直接利用概率的意义以及随机事件的定义分别分析得出答案.
【详解】A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上,错误,不符合题意;
B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨,错误,不符合题意;
C、“篮球队员在罚球线上投篮一次,投中”为随机事件,正确,符合题意;
D、“a是实数,|a|≥0”是必然事件,故此选项错误,不符合题意.
故选C.
【点睛】此题主要考查了概率的意义以及随机事件的定义,正确把握相关定义是解题关键.
5.C
【分析】首先设正方形的面积,再表示出阴影部分面积,然后可得概率.
【详解】解:设“东方模板”的面积为4,则阴影部分三角形面积为1,平行四边形面积为,
则点取自黑色部分的概率为:,
故选C.
【点睛】此题主要考查了概率,关键是表示图形的面积和阴影部分面积.
6.D
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号和大于3的情况,再利用概率公式即可求得答案.
【详解】解:根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和大于3的有6种,
∴两次摸出的小球标号的和大于3的概率是,
故选:D
【点睛】此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.C
【分析】利用列表法或树状图即可解决.
【详解】分别用r、b代表红色帽子、黑色帽子,用R、B、W分别代表红色围巾、黑色围巾、白色围巾,列表如下:
R B W
r rR rB rW
b bR bB bW
则所有可能的结果数为6种,其中恰好为红色帽子和红色围巾的结果数为1种,根据概率公式,恰好为红色帽子和红色围巾的概率是.
故选:C.
【点睛】本题考查了简单事件的概率,常用列表法或画树状图来求解.
8.D
【分析】根据随机事件发生的独立性,可得某次射击的结果与连续射靶100次的结果无关,所以针对某次射击,命中10环、9环、8环的可能性均等,据此解答即可.
【详解】根据随机事件发生的独立性,可得某次射击的结果与连续射靶100次的结果无关,所以针对某次射击,命中10环、9环、8环的可能性均等.如果再让他打靶次,都有可能.
故选:D.
【点睛】此题主要考查了随机事件发生的独立性问题的应用.
9.D
【分析】根据利用频率估计概率得到实验的概率在0.33左右,再分别计算出四个选项中的概率,再进行判断.
【详解】A、抛一枚硬币,出现正面的概率是,不符合题意;
B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是,不符合题意;
C、抛一个质地均匀的正六面体骰子(六个面上分别标1,2,3,4,5,6),向上的面点数是5的概率是,不符合题意;
D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率是,符合题意,
故选:D.
【点睛】此题考查频率估计概率,计算简单事件的概率,正确理解题意计算出各事件的概率是解题的关键.
10.D
【分析】根据事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,在一定条件下,可能发生也可能不发生的事件,称为随机事件进行分析即可.
【详解】A、两枚骰子向上一面的点数之和大于1,是必然事件,故此选项错误;
B、两枚骰子向上一面的点数之和等于1,是不可能事件,故此选项错误;
C、两枚骰子向上一面的点数之和大于12,是不可能事件,故此选项错误;
D、两枚骰子向上一面的点数之和等于12,是随机事件,故此选项正确;
故选:D.
【点睛】此题主要考查了随机事件的判断,关键是掌握随机事件,确定性事件的定义.
11.
【分析】列举出所有情况,看球的顺序依次是“红黄蓝”的情况数占所有情况数的多少即可.
【详解】解:画出树形图:
共有27种情况,球的顺序依次是“红黄蓝”的情况数有1种,所以概率为.
故答案为:.
【点睛】考查用列树状图的方法解决概率问题;得到球的顺序依次是“红黄蓝”的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.
12.
【分析】根据概率公式直接求解即可.
【详解】共6个数字,其中小于3的数有2个
投掷一次,朝上的面的数字小于3的概率为.
故答案为:
【点睛】本题考查了简单概率公式的计算,熟悉概率公式是解题的关键.
13.0.9
【分析】由题意根据概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率进行分析即可.
【详解】解:概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率,
∴这种幼树移植成活率的概率约为0.9.
故答案为:0.9.
【点睛】本题主要考查利用频率估计概率,大量反复试验下频率稳定值即概率.注意掌握频率=所求情况数与总情况数之比.
14.##0.4
【分析】先确定无理数的个数,再除以总个数.
【详解】解:,是无理数,
(恰好是无理数).
故答案为:.
【点睛】本题主要考查了概率公式及无理数,熟练掌握概率公式及无理数的定义进行计算是解决本题的关键.
15. (1),(2) (3)
【分析】根据事件的分类判断,随机事件就是可能发生也可能不发生的事件,必然事件就是一定发生的事件,根据定义即可解决.
【详解】(1)明天是晴天,无法确定是随机事件;
(2)黑暗中从一串不同的钥匙中随意摸出一把,用它打开了门,无法确定是随机事件;
(3)某小组有13名同学,至少有2名同学的生日在同一个月,是确定事件是必然事件;
(4)在标准大气压下,温度低于0℃时冰融化,是不可能事件,在这些事件中属于随机事件的有(1),(2);属于必然事件的有(3).
故答案为(1),(2);(3).
【点睛】本题考查了必然事件、不可能事件、随机事件的概念,必然事件指在一定条件下一定发生的事件,不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,难度适中.
16.##0.4
【分析】根据题意可知有理数有-31、,共2个,根据概率公式即可求解
【详解】解:在、、-31、、0.101001001…(相邻两个1间依次多1个0)五个实数中,-31、是有理数,
∴任意取一张,抽到有理数的概率是
故答案为:
【点睛】本题考查了实数的分类,根据概率公式求概率,理解题意是解题的关键.
17.0.84
【分析】观察表格合格的频率趋近于0.84,从而由此得到口罩合格的概率即可.
【详解】解:∵随着抽样的增大,合格的频率趋近于0.84,
∴估计从该批次口罩中任抽一只口罩是合格品的概率为0.84.
故答案为:0.84.
【点睛】本题考查了用频率估计概率,解题关键是熟练运用频率估计概率解决问题.
18.(1)详见解析;(2).
【分析】(1)根据题意可以写出所有的可能性;
(2)根据(1)中的结果可以得到乙本局获胜的可能性,从而可以解答本题.
【详解】解:(1)由题意可得,每人随机取出手中的一张牌进行比较的所有情况是:
,,,,,,,,.
(2)由()知共有9种等可能的情况,学生乙获胜的情况有:,,,
所以学生乙一局比赛获胜的概率是:.
故答案为(1)见解析;(2).
【点睛】本题考查了列表法与树状图法,概率=所求情况数与总情况数之比.
19.(1);(2)见解析,
【分析】(1)这个事件中有10种等可能性,其中是6的有一种可能性,根据概率公式计算即可;
(2)画出树状图计算即可.
【详解】(1)∵这个事件中有10种等可能性,其中是6的有一种可能性,
∴数字是6的概率为,
故答案为:;
(2)解:画树状图如图所示:
∵共有12种等可能的结果,其中有一幅是祖冲之的画像有6种情况.
∴(其中有一幅是祖冲之).
【点睛】本题考查了概率公式计算,画树状图或列表法计算概率,熟练掌握概率计算公式,准确画出树状图或列表是解题的关键.
20.(1)
(2)
【分析】(1)利用例举法例举所有的等可能的情况数,再利用概率公式进行计算即可;
(2)先列表得到所有的等可能的情况数以及符合条件的情况数,再利用概率公式进行计算即可.
(1)
解:由甲一定参加比赛,再从其余3名学生中任意选取1名,共有甲、乙,甲、丙,甲、丁三种等可能,符合条件的情况数有1种,
∴甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是
(2)
列表如下:
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
所有所有的等可能的情况数有12种,符合条件的情况数有6种,
所以一定有乙的概率为:
【点睛】本题考查的是利用例举法,列表的方法求解简单随机事件的概率,概率公式的应用,掌握“例举法与列表法求解概率”是解本题的关键.
21.(1)本次参加抽样调查的居民有600人;(2)见解析;(3).
【分析】(1)用喜欢B类的人数除以它所占的百分比得到调查的总人数;
(2)先计算出喜欢C类的人数,再计算出喜欢A类的人数的百分比和喜欢C类的人数的百分比,然后补全条形统计图和扇形统计图;
(3)画树状图展示所有12种等可能的结果数,找出小明同时选中花生粽子和红枣粽子的结果数,然后根据概率公式求解.
【详解】(1)60÷10%=600,
所以本次参加抽样调查的居民有600人;
(2)喜欢C类的人数为600﹣180﹣60﹣240=120(人),
喜欢A类的人数的百分比为×100%=30%;
喜欢C类的人数的百分比为×100%=20%;
两幅统计图补充为:
(3)画树状图为:
共有12种等可能的结果数,其中小明同时选中花生粽子和红枣粽子的结果数为2,
所以小明同时选中花生粽子和红枣粽子的概率==.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
试卷第1页,共3页
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
