1.3 绝对值.ppt

课件18张PPT。绝对值 动手试一试
把公路看成一条直线,家作为原点, 规定向东为正,
1公里记作一个单位长度,请建立一条数轴并标出叶子
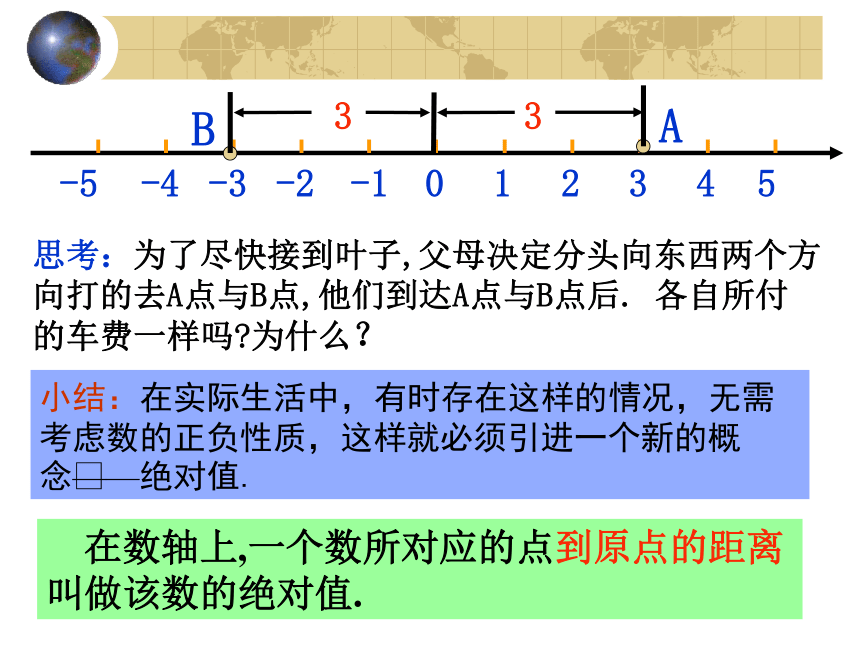
可能所在的位置 0 1 2 3 4 5 -1 -2 -3 -4 -5 叶子去同学家参加生日聚会 :妈妈,我是叶子, 九点钟回家,你和爸爸到解放路上离我们家3公里的站点来接我。 (注:叶子家就在解放路上，公路是东西朝向的) 叶子父母走出家门正准备打的时 他们犹豫了… AB思考：为了尽快接到叶子,父母决定分头向东西两个方向打的去A点与B点,他们到达A点与B点后. 各自所付
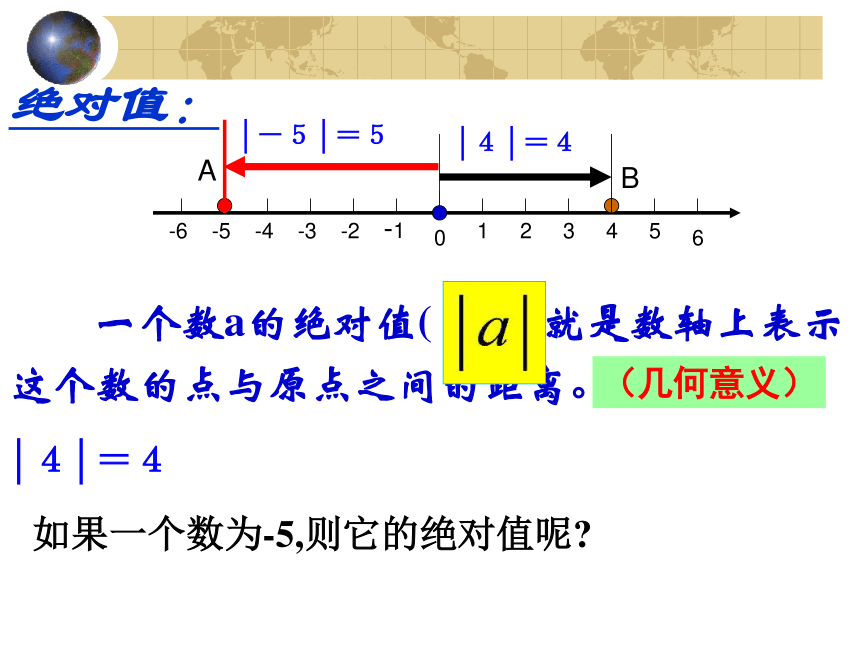
的车费一样吗?为什么？ 小结：在实际生活中，有时存在这样的情况，无需考虑数的正负性质，这样就必须引进一个新的概念——绝对值. 在数轴上,一个数所对应的点到原点的距离叫做该数的绝对值.AB3306 一个数a的绝对值( )就是数轴上表示这个数的点与原点之间的距离。-1-2-3-4-5-612345B
A│－５│＝５│４│＝４绝对值：│４│＝４如果一个数为-5,则它的绝对值呢?（几何意义） 1.表示+2.8的点与原点的距离是　　，
即+2.8的绝对值是　　,记作　　；
2.表示0的点与原点的距离是　 　，
即0的绝对值是　 　,记作　　；
3. 表示-7的点与原点的距离是　　，
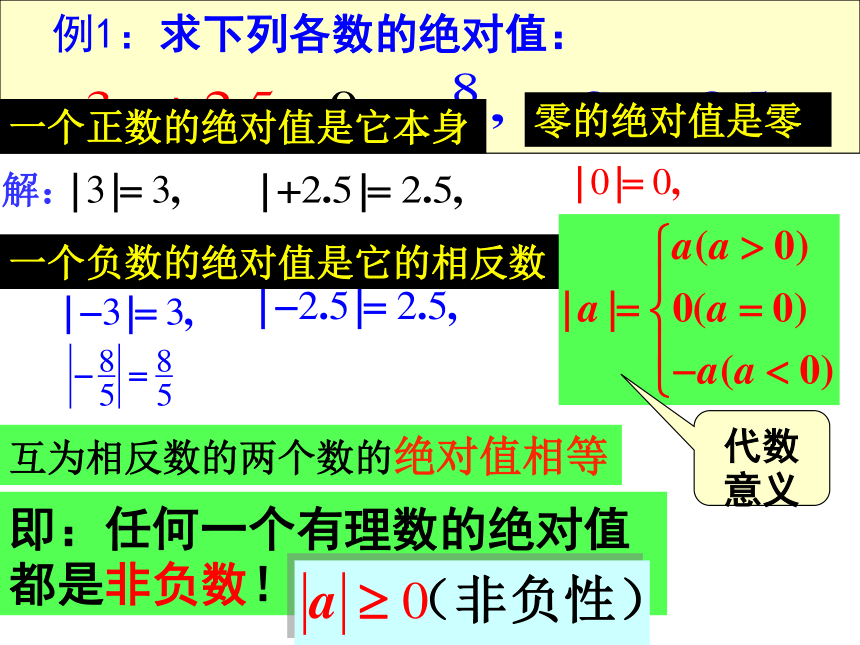
即-5的绝对值是　 　,记作　　； 口答2.82.8 例1：求下列各数的绝对值：解：一个正数的绝对值是它本身零的绝对值是零一个负数的绝对值是它的相反数互为相反数的两个数的绝对值相等即：任何一个有理数的绝对值都是非负数！代数意义1。若一个有理数的绝对值等于它的相反数，
那么这个数是（ ）
A 正数 B 负数 C 0 D 0或者负数(非正数)巩固加深2。绝对值最小的有理数是________计算下列各式：例 21.说出下列各数的绝对值：练习1练习2(2)绝对值小于 5 的整数有（ ）个。(3)绝对值不大于 7 的负整数是（ ）。9-1,-2,-3,-4,-5,-6,-7(4)若│a-4│+ │b│=0，那么a=___,b=___(1)若│m│=3，那么m=_______变一变+3和 -3 4和 -2 40练习3判断（1）一个数的绝对值一定是正数。 （ ）（2）一个数的绝对值不可能是负数。 （ ）（3）互为相反数的两个数，它们的绝对值
一定相等。 （ ）（4）绝对值是同一个正数的数有两个，且
它们是互为相反数。 （ ）×√√√0P17 T3文字叙述 ? 表达式叙述一个数的绝对值是它本身,这个数是( ).正数或零一个数的绝对值是它的相反数,这个数是( )负数或零如果 | a | = a , a ? 0 .如果 | a | = -a , a ? 0 .P17 T4 小结：1、绝对值的定义2、去绝对值的方法： 在数轴上，一个数所对应的点到原点的距离正数的绝对值是它本身; 负数的绝对值是它的相反数; 0 的绝对值是 0.3、任何数的绝对值都是______绝对值等于它本身的数是______绝对值等于它的相反数是______非负数非负数非正数议一议下列判断，正确的个数有 个。
(1)如果两个数相等,那么这两个数的绝对值一定相等；
(2)如果两个数不相等,那么这两个数的绝对值一定不相等；
(3)如果两个数的绝对值相等,那么这两个数一定相等；
(4)如果两个数的绝对值不相等,那么这两个数一定不相等拓展练习考一考：下面的说法是否正确？
（1）有理数的绝对值一定比0大
（2）有理数的相反数一定比0小
（3）如果两个数的绝对值相等,那么这两个数相等。
（4）互为相反数的两个数的绝对值相等。拓展练习拓展练习3.选择（1） m 是有理数时,下列说法中正确的是
(A) -m 是负数 (B) |m|是正数
(C) |-m|是非负数 (D) -|m|是负数（2）若 |a| > a , 则 a 是
(A) 正数 (B) 负数
(C) 非正数 (D) 非负数（3）一个数的相反数的绝对值是正数,这个数一定是
(A) 非正数 (B) 非负数
(C) 非零数 (D)不能确定拓展练习