2022-2023学年浙教版八年级数学下册5.1 矩形同步练习(含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学下册5.1 矩形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 578.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 17:59:57 | ||
图片预览


文档简介
浙教版 八下(浙教版)第5章 特殊平行四边形5.1 矩形
一、选择题(共9小题)
1. 下列说法中,正确的是
A. 两组对角分别相等的四边形是矩形
B. 两个角是直角的四边形是矩形
C. 一个角是直角的平行四边形是矩形
D. 一个角是直角,一组对边相等的四边形是矩形
2. 如图所示,四边形 的对角线 , 相交于点 ,给出下列条件:① ;② ;③ ;④ ;⑤ ;⑥ .不能使四边形 成为矩形的是
A. ①②③ B. ②③④ C. ②⑤⑥ D. ④⑤⑥
3. 已知四边形 的两条对角线 , 互相垂直,,,, 分别是四边形 各边的中点.若 ,,则四边形 的面积为
A. B.
C. D. 条件不足,无法计算
4. 如图所示,在 中, 的中垂线交 , 于点 ,, 交 延长线于点 ,若 ,,,则四边形 的面积是
A. B. C. D.
5. 在平行四边形 中,, 是两条对角线,如果添加一个条件,即可推出平行四边形 是矩形,那么这个条件可以是
A. B. C. D.
6. 在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是
A. 测量对角线是否相互平分 B. 测量两组对边是否分别相等
C. 测量对角线是否相等 D. 测量其中三个角是否都为直角
7. 平行四边形内角平分线能够围成的四边形是
A. 梯形 B. 矩形
C. 正方形 D. 不是平行四边形
8. 如图,四边形 为平行四边形,延长 到点 ,使 ,连接 ,,.添加一个条件,不能使四边形 成为矩形的是
A. B. C. D.
9. 如图,在 中,,,, 是 上一动点,过点 作 于点 , 于点 ,连接 ,则线段 的最小值是
A. B. C. D.
二、填空题(共6小题)
10. 如图所示,在平行四边形 中,对角线 , 相交于点 ,且 ,.则 .
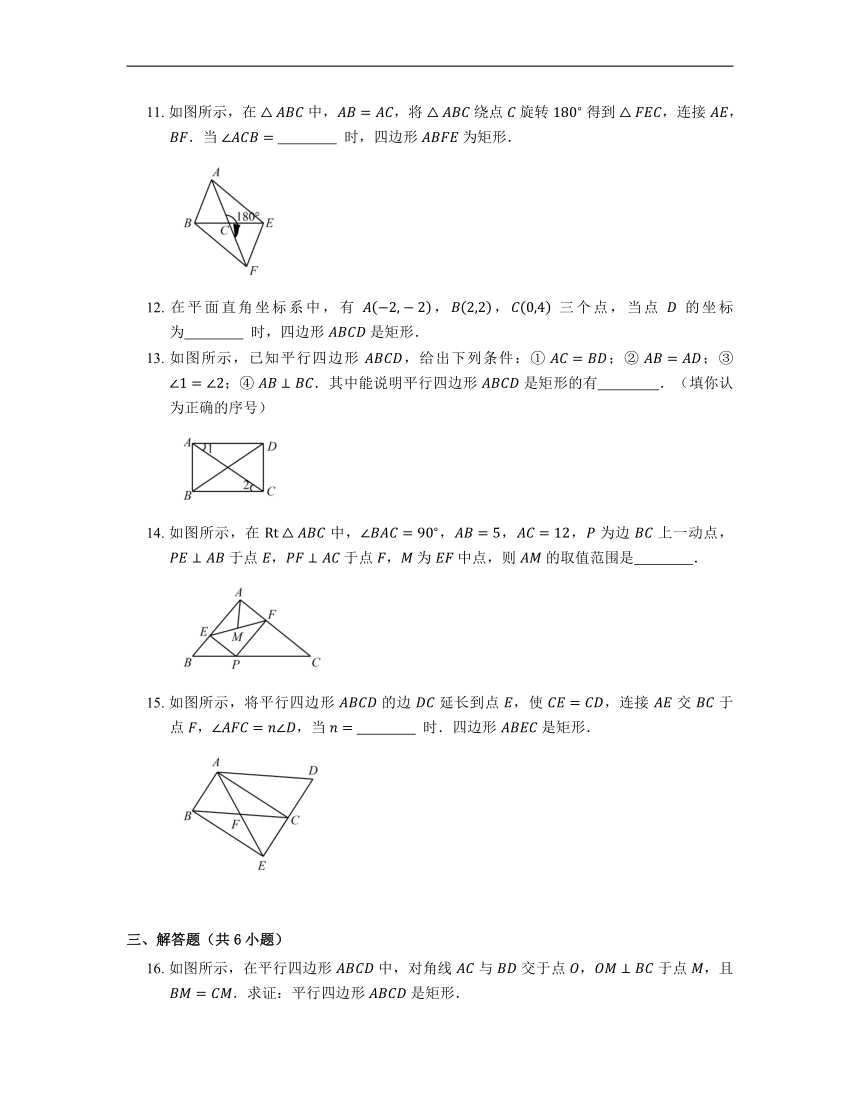
11. 如图所示,在 中,,将 绕点 旋转 得到 ,连接 ,.当 时,四边形 为矩形.
12. 在平面直角坐标系中,有 ,, 三个点,当点 的坐标为 时,四边形 是矩形.
13. 如图所示,已知平行四边形 ,给出下列条件:① ;② ;③ ;④ .其中能说明平行四边形 是矩形的有 .(填你认为正确的序号)
14. 如图所示,在 中,,,, 为边 上一动点, 于点 , 于点 , 为 中点,则 的取值范围是 .
15. 如图所示,将平行四边形 的边 延长到点 ,使 ,连接 交 于点 ,,当 时.四边形 是矩形.
三、解答题(共6小题)
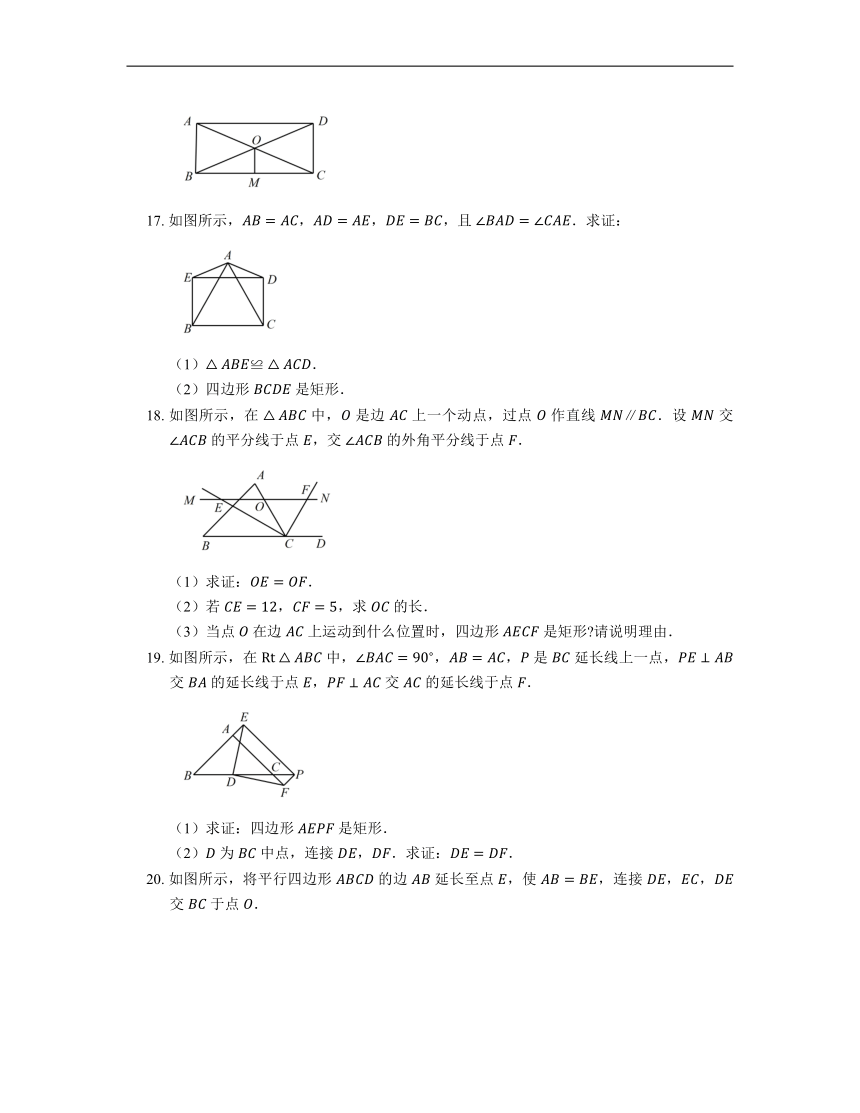
16. 如图所示,在平行四边形 中,对角线 与 交于点 , 于点 ,且 .求证:平行四边形 是矩形.
17. 如图所示,,,,且 .求证:
(1).
(2)四边形 是矩形.
18. 如图所示,在 中, 是边 上一个动点,过点 作直线 .设 交 的平分线于点 ,交 的外角平分线于点 .
(1)求证:.
(2)若 ,,求 的长.
(3)当点 在边 上运动到什么位置时,四边形 是矩形 请说明理由.
19. 如图所示,在 中,,, 是 延长线上一点, 交 的延长线于点 , 交 的延长线于点 .
(1)求证:四边形 是矩形.
(2) 为 中点,连接 ,.求证:.
20. 如图所示,将平行四边形 的边 延长至点 ,使 ,连接 ,, 交 于点 .
(1)求证:;
(2)连接 ,若 ,求证:四边形 是矩形.
21. 已知矩形 和点 ,当点 在 上任一位置(如图 1所示)时,易证得结论 .请你探究:当点 分别在图 2 、图 3中的位置时,,, 和 又有怎样的数量关系 请你写出对上述两种情况的探究结论,并利用图 2证明你的结论.
对图 2的探究结论为 ;对图 3的探究结论为 .
答案
1. C
2. C
3. C
4. A
5. B
6. D
7. B
8. B
9. B
10.
11.
12.
13. ①④
14.
15.
16. 四边形 是平行四边形,
,.
又 ,,
.
.
平行四边形 是矩形.
17. (1) ,
,
在 和 中,
.
(2) ,
,
,
四边形 为平行四边形.
,
.
,
.
.
四边形 为平行四边形,
.
.
.
四边形 是矩形.
18. (1) 交 的平分线于点 ,交 的外角平分线于点 ,
,.
,
,.
,.
,.
.
(2) 如图所示,
,,
.
,,
.
.
(3) 当点 在边 上运动到 中点时,四边形 是矩形.理由如下:
当 为 的中点时,.
,
四边形 是平行四边形,
,
平行四边形 是矩形.
19. (1) ,,,
四边形 是矩形.
(2) 连接 .
,, 为 中点,
,.
又由(1)知 , 是等腰直角三角形,
.
.
.
20. (1) 在平行四边形 中,,,,则 .
又因为 ,
所以 .
所以四边形 为平行四边形.
所以 .
在 与 中,
所以 .
(2) 由(1)知,四边形 为平行四边形,
则 ,.
因为四边形 为平行四边形,
所以 ,
即 .
又因为 ,,
所以 .
所以 .
所以 ,即 ,
所以平行四边形 为矩形.
21. 结论均是 ;
证明:如图所示,过点 作 ,交 于点 ,交 于点 .
所以四边形 和四边形 均为矩形,
根据(1)中的结论可得,在矩形 中有 ,在矩形 中有 ,两式相加得 ,
所以 .
一、选择题(共9小题)
1. 下列说法中,正确的是
A. 两组对角分别相等的四边形是矩形
B. 两个角是直角的四边形是矩形
C. 一个角是直角的平行四边形是矩形
D. 一个角是直角,一组对边相等的四边形是矩形
2. 如图所示,四边形 的对角线 , 相交于点 ,给出下列条件:① ;② ;③ ;④ ;⑤ ;⑥ .不能使四边形 成为矩形的是
A. ①②③ B. ②③④ C. ②⑤⑥ D. ④⑤⑥
3. 已知四边形 的两条对角线 , 互相垂直,,,, 分别是四边形 各边的中点.若 ,,则四边形 的面积为
A. B.
C. D. 条件不足,无法计算
4. 如图所示,在 中, 的中垂线交 , 于点 ,, 交 延长线于点 ,若 ,,,则四边形 的面积是
A. B. C. D.
5. 在平行四边形 中,, 是两条对角线,如果添加一个条件,即可推出平行四边形 是矩形,那么这个条件可以是
A. B. C. D.
6. 在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是
A. 测量对角线是否相互平分 B. 测量两组对边是否分别相等
C. 测量对角线是否相等 D. 测量其中三个角是否都为直角
7. 平行四边形内角平分线能够围成的四边形是
A. 梯形 B. 矩形
C. 正方形 D. 不是平行四边形
8. 如图,四边形 为平行四边形,延长 到点 ,使 ,连接 ,,.添加一个条件,不能使四边形 成为矩形的是
A. B. C. D.
9. 如图,在 中,,,, 是 上一动点,过点 作 于点 , 于点 ,连接 ,则线段 的最小值是
A. B. C. D.
二、填空题(共6小题)
10. 如图所示,在平行四边形 中,对角线 , 相交于点 ,且 ,.则 .
11. 如图所示,在 中,,将 绕点 旋转 得到 ,连接 ,.当 时,四边形 为矩形.
12. 在平面直角坐标系中,有 ,, 三个点,当点 的坐标为 时,四边形 是矩形.
13. 如图所示,已知平行四边形 ,给出下列条件:① ;② ;③ ;④ .其中能说明平行四边形 是矩形的有 .(填你认为正确的序号)
14. 如图所示,在 中,,,, 为边 上一动点, 于点 , 于点 , 为 中点,则 的取值范围是 .
15. 如图所示,将平行四边形 的边 延长到点 ,使 ,连接 交 于点 ,,当 时.四边形 是矩形.
三、解答题(共6小题)
16. 如图所示,在平行四边形 中,对角线 与 交于点 , 于点 ,且 .求证:平行四边形 是矩形.
17. 如图所示,,,,且 .求证:
(1).
(2)四边形 是矩形.
18. 如图所示,在 中, 是边 上一个动点,过点 作直线 .设 交 的平分线于点 ,交 的外角平分线于点 .
(1)求证:.
(2)若 ,,求 的长.
(3)当点 在边 上运动到什么位置时,四边形 是矩形 请说明理由.
19. 如图所示,在 中,,, 是 延长线上一点, 交 的延长线于点 , 交 的延长线于点 .
(1)求证:四边形 是矩形.
(2) 为 中点,连接 ,.求证:.
20. 如图所示,将平行四边形 的边 延长至点 ,使 ,连接 ,, 交 于点 .
(1)求证:;
(2)连接 ,若 ,求证:四边形 是矩形.
21. 已知矩形 和点 ,当点 在 上任一位置(如图 1所示)时,易证得结论 .请你探究:当点 分别在图 2 、图 3中的位置时,,, 和 又有怎样的数量关系 请你写出对上述两种情况的探究结论,并利用图 2证明你的结论.
对图 2的探究结论为 ;对图 3的探究结论为 .
答案
1. C
2. C
3. C
4. A
5. B
6. D
7. B
8. B
9. B
10.
11.
12.
13. ①④
14.
15.
16. 四边形 是平行四边形,
,.
又 ,,
.
.
平行四边形 是矩形.
17. (1) ,
,
在 和 中,
.
(2) ,
,
,
四边形 为平行四边形.
,
.
,
.
.
四边形 为平行四边形,
.
.
.
四边形 是矩形.
18. (1) 交 的平分线于点 ,交 的外角平分线于点 ,
,.
,
,.
,.
,.
.
(2) 如图所示,
,,
.
,,
.
.
(3) 当点 在边 上运动到 中点时,四边形 是矩形.理由如下:
当 为 的中点时,.
,
四边形 是平行四边形,
,
平行四边形 是矩形.
19. (1) ,,,
四边形 是矩形.
(2) 连接 .
,, 为 中点,
,.
又由(1)知 , 是等腰直角三角形,
.
.
.
20. (1) 在平行四边形 中,,,,则 .
又因为 ,
所以 .
所以四边形 为平行四边形.
所以 .
在 与 中,
所以 .
(2) 由(1)知,四边形 为平行四边形,
则 ,.
因为四边形 为平行四边形,
所以 ,
即 .
又因为 ,,
所以 .
所以 .
所以 ,即 ,
所以平行四边形 为矩形.
21. 结论均是 ;
证明:如图所示,过点 作 ,交 于点 ,交 于点 .
所以四边形 和四边形 均为矩形,
根据(1)中的结论可得,在矩形 中有 ,在矩形 中有 ,两式相加得 ,
所以 .
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
