第一章三角形初步知识

每周一练：第二周（第一章三角形初步知识）
一、选择题
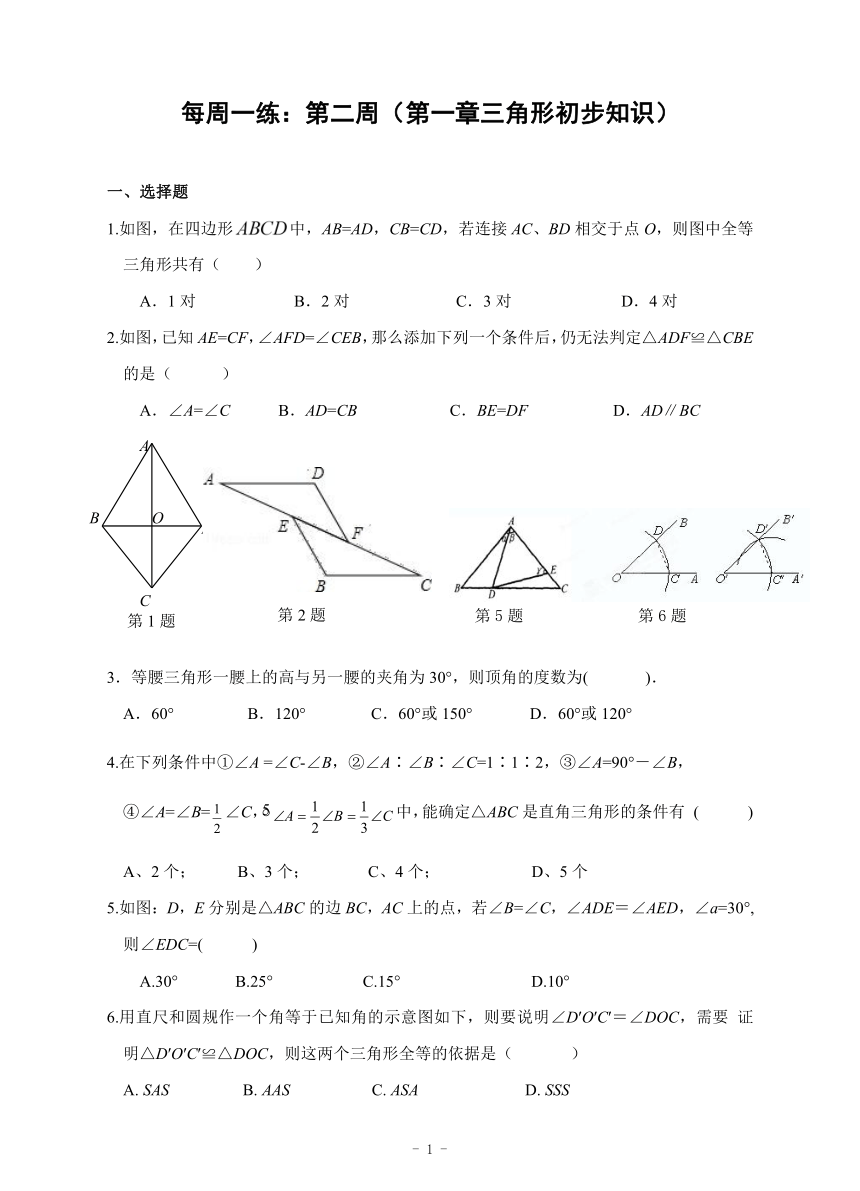
1.如图，在四边形中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）
A．1对 B．2对 C．3对 D．4对
2.如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　 　）
A．∠A=∠C B．AD=CB C．BE=DF D．AD∥BC
3．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为( )．
A．60°　　　 B．120°　　　 C．60°或150°　　　 D．60°或120°
4.在下列条件中①∠A =∠C-∠B，②∠A∶∠B∶∠C=1∶1∶2，③∠A=90°－∠B，
④∠A=∠B=∠C，中，能确定△ABC是直角三角形的条件有 ( )
A、2个； B、3个； C、4个； D、5个
5.如图：D，E分别是△ABC的边BC，AC上的点，若∠B=∠C，∠ADE＝∠AED，∠a=30,则∠EDC=( )
A.30 B.25 C.15 D.10
6.用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠D′O′C′＝∠DOC，需要 证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（ ）
A. SAS B. AAS C. ASA D. SSS
7.对于三角形的内角,下列判断中不正确的是( )；
A.至少有两个锐角 B.最多有一个直角
C.必有一个角大于600 D.至少有一个角不小于600
8.下列四组中一定是全等三角形的是( )；
A．两条边对应相等的两个锐角三角形 B．面积相等的两个钝角三角形
C．斜边相等的两个直角三角形 D．周长相等的两个等边三角形
9. 如图,在ΔABC中,BC边上的垂直平分线交AC于点D,
已知AB=3,AC=7,BC=8,则ΔABD的周长为( )
A.10 B.11 C.15 D.12
10．在△ABC中，∠A=2∠B=4∠C，则△ABC为（ ）
A.锐角三角形 B.钝角三角形 C.直角三角形 D.都有可能
二．填空题
11．已知三角形的三边长分别是3、x、9，则化简=
12．如图，在 ABC中，AD是BC边上的中线，已知AB=7 cm ，AC=5cm，则 ABD和 ACD
的周长差为 cm．
如图，∠A=50°，∠ABO=28°，∠ACO=32°，则∠BDC= ，∠BOC=
14.如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为　____　（答案不唯一，只需填一个）
15．在△ABC中，AB＝3，BC＝7，则AC边上中线BD的取值范围是________
16.已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：
①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；其中结论正确是_____________(填序号）
三、解答题
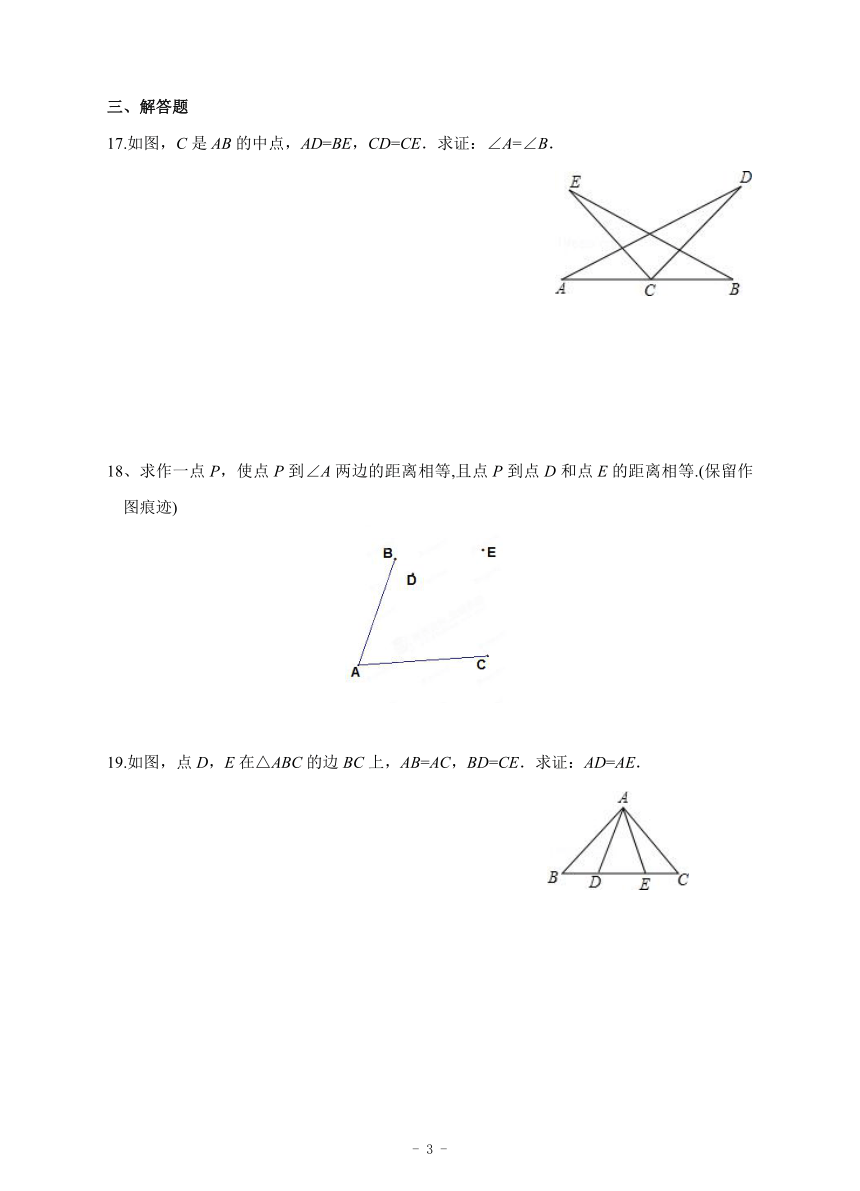
17.如图，C是AB的中点，AD=BE，CD=CE．求证：∠A=∠B．
( http: / / )
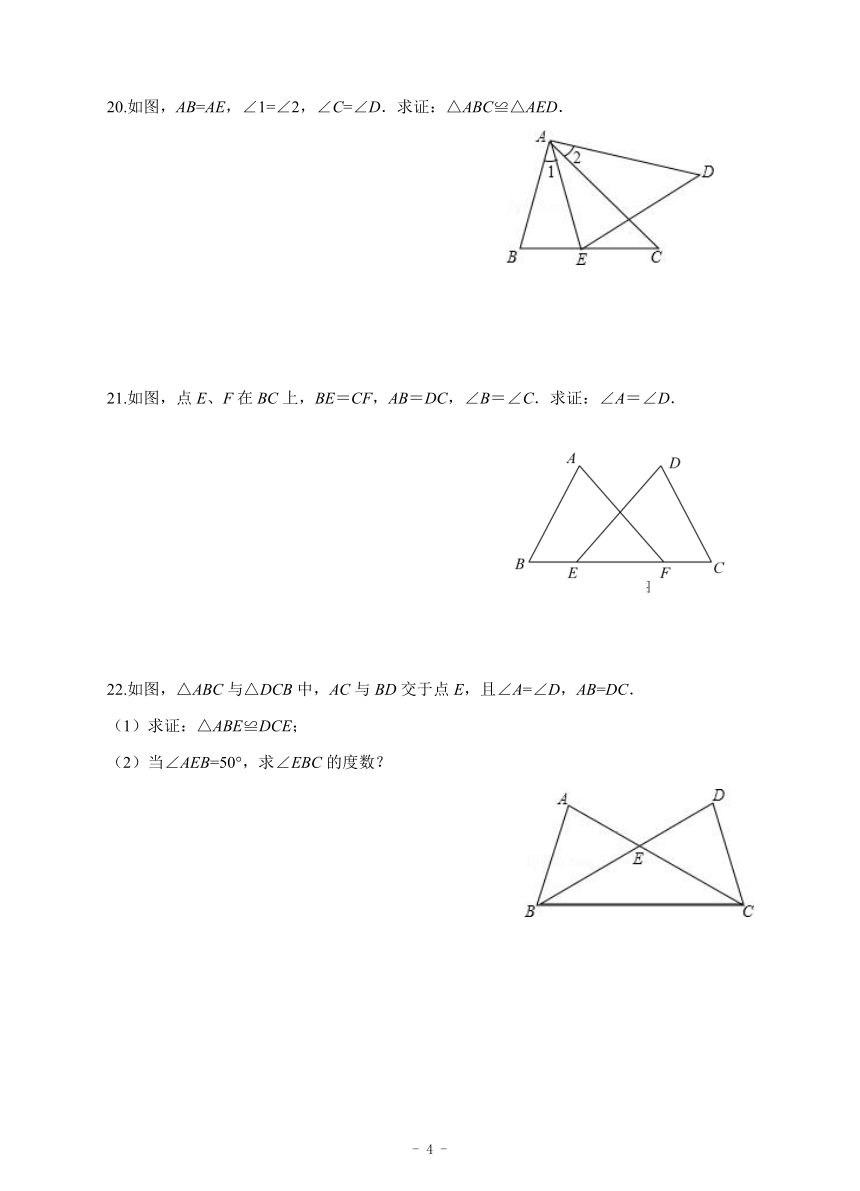
求作一点P，使点P到∠A两边的距离相等,且点P到点D和点E的距离相等.(保留作 图痕迹)
19.如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．
( http: / / )
20.如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．
( http: / / )
21.如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．
22.如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．
（1）求证：△ABE≌DCE；
（2）当∠AEB=50°，求∠EBC的度数？
( http: / / )
23..课本指出：公认的真命题称为公理，除了公理外，其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实．
（1）叙述三角形全等的判定方法中的推论AAS；
（2）证明推论AAS．
要求：叙述推论用文字表达；用图形中的符号表达已知、求证，并证明，证明对各步骤要注明依据．
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D C D C D A B
二．填空题
11. 8 12. 2 13. 14. AC=CD(答案不唯一）
15. 16. ①②③
解答题
17.证明：∵C是AB的中点，∴AC=BC，
∴△ACD≌△BCE（SSS），
∴∠A=∠B（全等三角形对应角相等）．
19.证明：∵AB=AC（已知）
∴∠B=∠C
在△ABD与△ACE中，
∴△ABD≌△ACE（SAS），
∴AD=AE（全等三角形对应边相等）
20. 证明：∵∠1=∠2（已知）
∴∠1+∠EAC=∠2+∠EAC，
即∠BAC=∠EAD，
∵在△ABC和△AED中，
∴△ABC≌△AED（AAS）．
21.证明：∵BE＝CF（已知），∴BE+EF＝CF+EF，即BF＝CE．
在△ABF和△DCE中，
∴△ABF≌△DCE（SAS)，
∴∠A＝∠D（全等三角形对应角相等）
22.（1）证明：∵在△ABE和△DCE中
∴△ABE≌△DCE（AAS）；
（2）解：∵△ABE≌△DCE，
∴BE=EC，
∴∠EBC=∠ECB，
∵∠EBC+∠ECB=∠AEB=50°，
∴∠EBC=25°．
23.解：（1）三角形全等的判定方法中的推论AAS指的是：两边及其夹角分别对应相等的两个三角形全等．
（2）已知：在△ABC与△DEF中，∠A=∠D，∠C=∠F，BC=EF．
求证：△ABC≌△DEF．
证明：如图，在△ABC与△DEF中，∠A=∠D，∠C=∠F（已知），
∴∠A+∠C=∠D+∠F（等量代换）．
又∵∠A+∠B+∠C=180°，∠D+∠E+∠F=180°（三角形内角和定理），
∴∠B=∠E．
∴在△ABC与△DEF中，，
∴△ABC≌△DEF（ASA）．
第2题
B
C
D
A
O
第1题
第5题 第6题
第16题
第14题
A
B
C
D
第12题
第13题
A
B
C
D
E
F
第23题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
- 4 -