第一章三角形初步知识综合

每周一练：第三周（第一章三角形初步知识综合）
选择题
一个三角形的两边长分别是2cm和9cm，第三边的长是一个奇数，则第三边长为（ )
A、5cm B、7cm C、9cm D、11cm
2..有下列关于两个三角形全等的说法: （1）三个角对应相等的两个三角形全等;
（2）三条边对应相等的两个三角形全等;（3）两角与一边对应相等的两个三角形全等;
（4）两边和一角对应相等的两个三角形全等.其中正确的个数是：（　　）
A． 1 B. 2 C. 3 D. 4
3．三角形的高( )．
A. 一定在三角形的内部 B. 至少有两条在三角形的内部
C. 或者都在三角形的内部，或者有两条在三角形的外部；D. 以上都不对
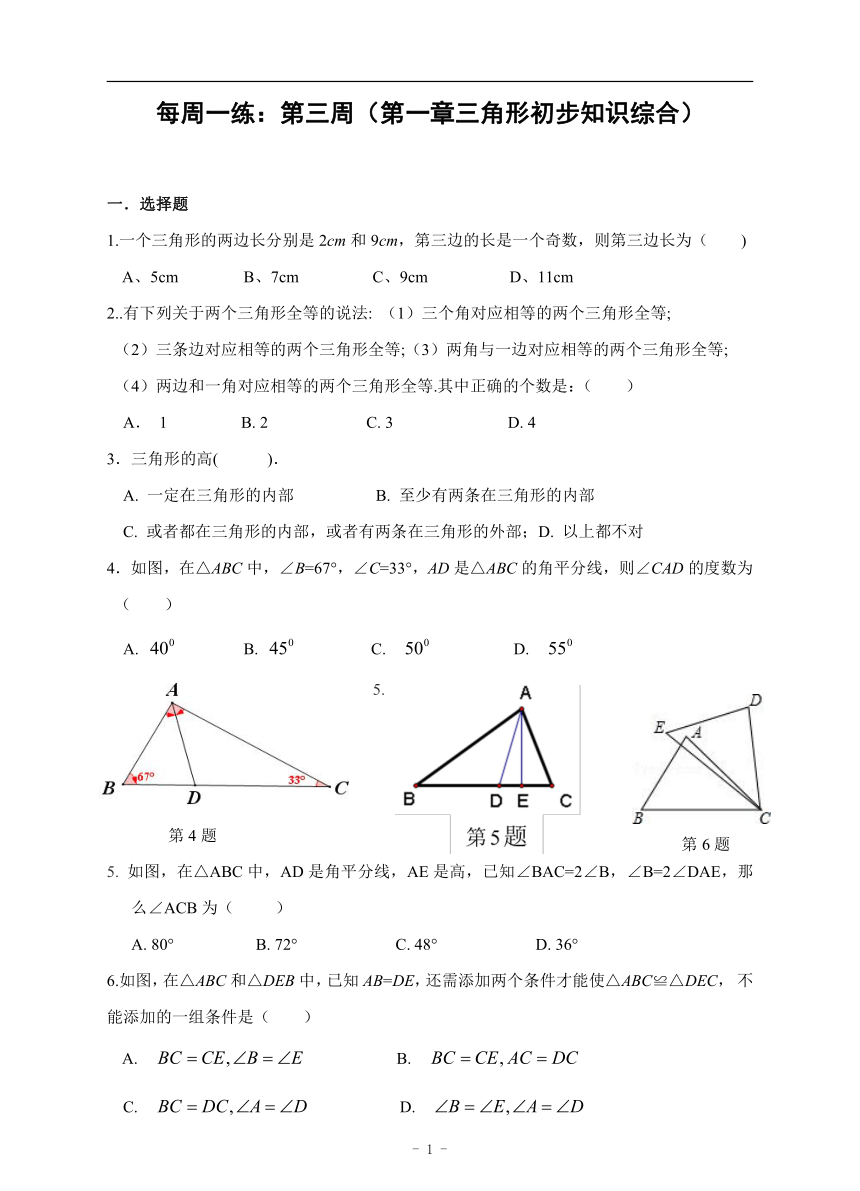
4．如图，在△ABC中，∠B=67°，∠C=33°，AD是△ABC的角平分线，则∠CAD的度数为（　　）
A. B. C. D.
5. 如图，在△ABC中，AD是角平分线，AE是高，已知∠BAC=2∠B，∠B=2∠DAE，那么∠ACB为（ ）
A. 80° B. 72° C. 48° D. 36°
如图，在△ABC和△DEB中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC， 不能添加的一组条件是（　　）
A. B.
C. D.
7. 如图，∠1=∠2，∠C=∠B，结论中不正确的是（ ）
A. △DAB≌△DAC B. △DEA≌△DFA C. CD=DE D. ∠AED=∠AFD
如图，PD⊥AB, PE⊥AC, 垂足分别为D , E，且AP平分∠BAC，则△APD与△APE全
等的理由是（ ）
A、SAS B、ASA C、SSS D、AAS
9.如图，在△ABC中，AB=AC，AB的中垂线DE交AC于点D，交AB于E点，如果BC=10，△BDC的周长为22，那么△ABC的周长是（ ）
A、24 B、30 C、32 D、34
如图，在△ABC中，∠ABC与∠ACB的角平分线交于点O，且∠A＝α，则∠BOC
的度数是（ ）
A. B. C. D.
二、填空题
11.如图，A，B，C三点在同一条直线上，∠A=∠C=90°，AB=CD，请添加一个适当的条件　 　，使得△EAB≌△BCD．
12.设△ABC的三边为a、b、c，化简
13.命题：对顶角相等，改写成“如果......那么......”的形式为_______________
14．已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角为70°，则∠BAC＝________°
15..如图，D是△ABC内任意一点，连接DA、DB、DC.试说明：DA+DB+DC> (AB+BC+CA)
理由_________________________________________________________________.
16.如图，把矩形ABCD沿AM折叠，使D点落在BC上的N点处，如果AD=cm，
DM=5cm，∠DAM=30°，则AN=_____cm，NM=______cm，∠BNA=_________度；
三、解答题
17.已知四边形ABCD是平行四边形（如图），把△ABD沿对角线BD翻折180°得到△AˊBD.
利用尺规作出△AˊBD.（要求保留作图痕迹，不写作法）；
（2）设D Aˊ 与BC交于点E，求证：△BAˊE≌△DCE.
18.如图，在中， ，点是边上的一点，，且， 过点作交于点。
求证：
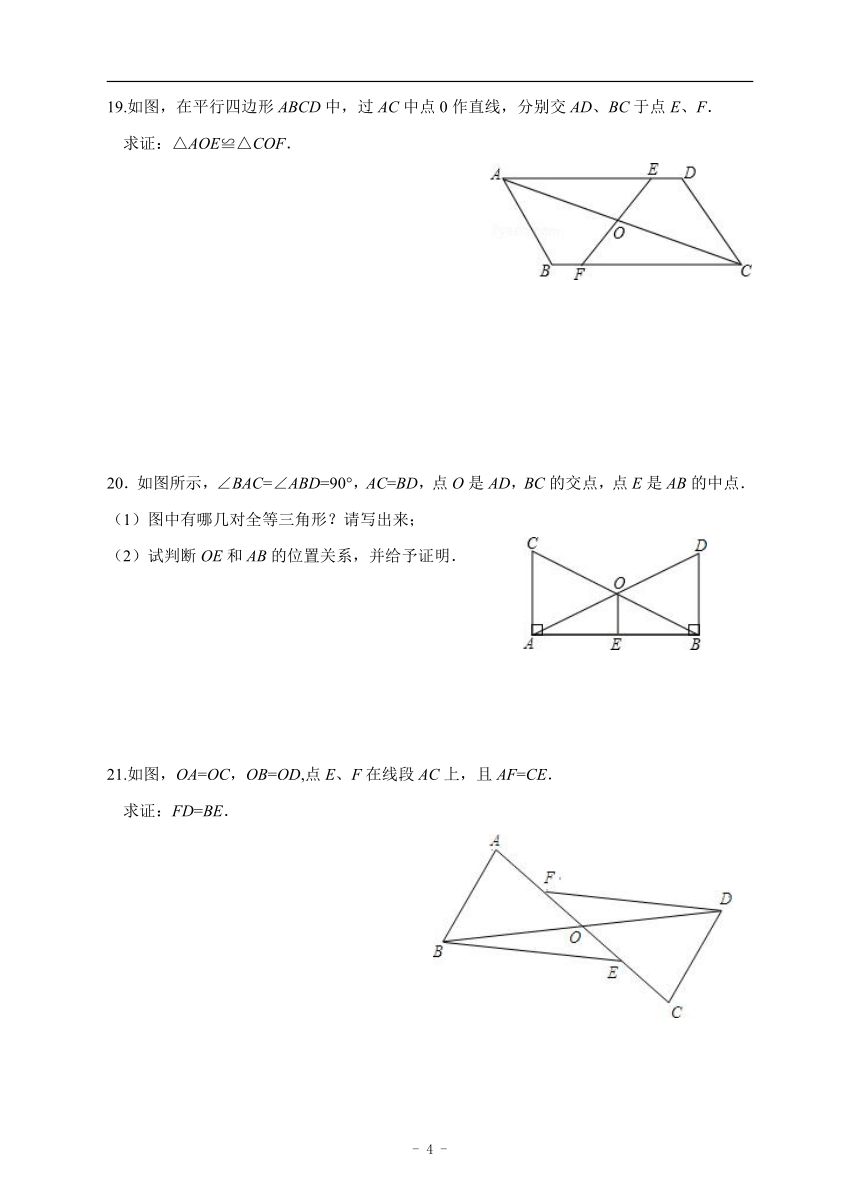
19.如图，在平行四边形ABCD中，过AC中点0作直线，分别交AD、BC于点E、F．
求证：△AOE≌△COF．
20．如图所示，∠BAC=∠ABD=90°，AC=BD，点O是AD，BC的交点，点E是AB的中点．]
（1）图中有哪几对全等三角形？请写出来；
（2）试判断OE和AB的位置关系，并给予证明．
21.如图，OA=OC，OB=OD,点E、F在线段AC上，且AF=CE．
求证：FD=BE．
22.如图正方形ABCD的边长为4，E、F分别为DC、BC中点．
（1）求证：△ADE≌△ABF．（2）求△AEF的面积．
23.如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
（1）求证：CE=CF；
（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D A A C C D D B
二、填空题
AE=CB 12. a+b+c 13.如果两个角是对顶角那么这两个角相等
14. .
16. 5 60
三、解答题
17.解：（1）如图：①作∠A′BD=∠ABD，
②以B为圆心，AB长为半径画弧，交BA′于点A′，
③连接BA′，DA′，
则△A′BD即为所求；
（2）∵四边形ABCD是平行四边形，
∴AB=CD，∠BAD=∠C，
由折叠的性质可得：∠BA′D=∠BAD，A′B=AB，
∴∠BA′D=∠C，A′B=CD，
在△BA′E和△DCE中，
，
∴△BA′E≌△DCE（AAS）．
18.证明：如图，
(两直线平行，同位角相等)
又，
在中
19.证明：∵AD∥BC，
∴∠EAO=∠FCO．
又∵∠AOE=∠COF，OA=OC，
在△AOE和△COF中，
，
∴△AOE≌△COF．
解：（1）△ABC≌△BAD，△AOE≌△BOE，△AOC≌△BOD；
（2）OE⊥AB．理由如下：
∵在Rt△ABC和Rt△BAD中，AC=BD，∠BAC=∠ABD，AB=BA，
∴△ABC≌△BAD，
∴∠DAB=∠CBA，
∴OA=OB，
∵点E是AB的中点，
∴OE⊥AB．
21.证明：∵OB=OD，OA=OC，
∵AF=CE，
∴OF=OE，
∵在△DOF和△BOE中
∴△DOF≌△BOE（SAS），
∴FD=BE(全等三角形对应边相等）．
22.（1）证明：∵四边形ABCD为正方形，
∴AB=AD，∠=90°，DC=CB，
∵E、F为DC、BC中点，
∴DE=DC，BF=BC，
∴DE=BF，
∵在△ADE和△ABF中，
，
∴△ADE≌△ABF（SAS）；
（2）解：由题知△ABF、△ADE、△CEF均为直角三角形，
且AB=AD=4，DE=BF=×4=2，CE=CF=×4=2，
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF
=4×4﹣×4×2﹣×4×2﹣×2×2=6．
23.（1）证明：在正方形ABCD中，
∵BC=CD，∠B=∠CDF，BE=DF，
∴△CBE≌△CDF（SAS）．
∴CE=CF．
（2）解：GE=BE+GD成立．
理由是：∵由（1）得：△CBE≌△CDF，
∴∠BCE=∠DCF，
∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，
又∠GCE=45°，∴∠GCF=∠GCE=45°．
∵CE=CF，∠GCE=∠GCF，GC=GC，
∴△ECG≌△FCG（SAS）．
∴GE=GF．
∴GE=DF+GD=BE+GD．
第6题
第4题
第4题
第8题
第9题
第10题
第7题
A
B
C
D
N
M
A
B
C
D
第11题
第15题
第16题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
- 1 -