1.3证明（1）

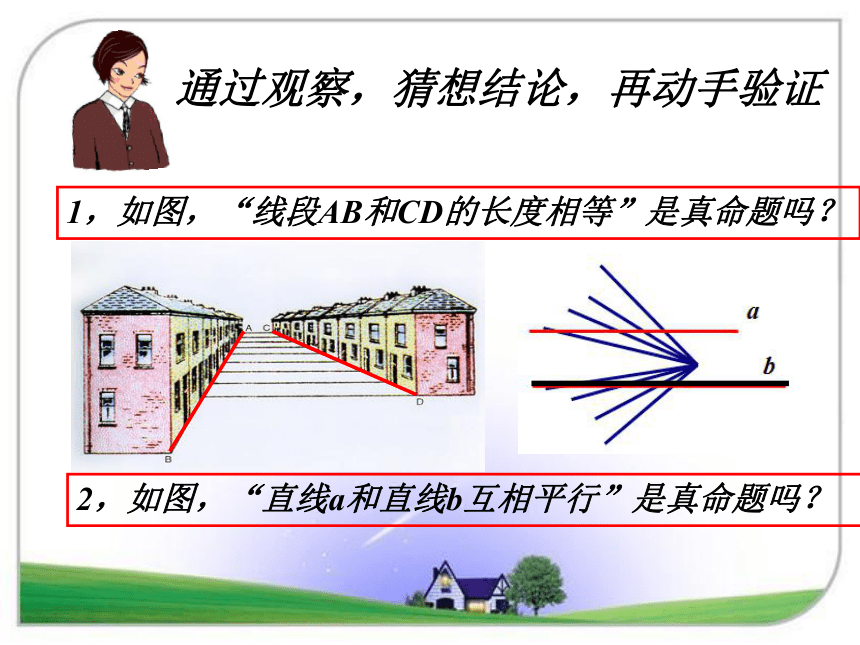
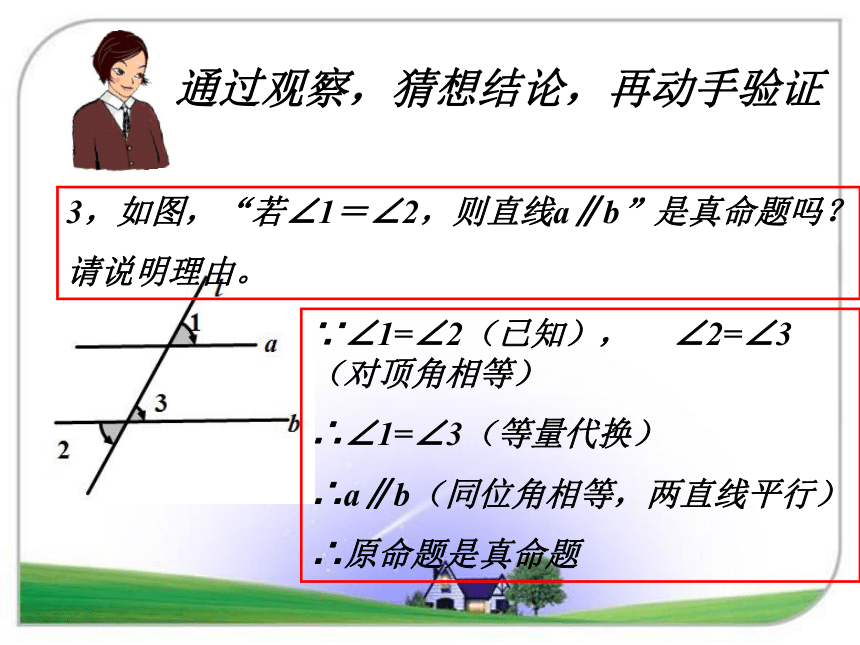
课件11张PPT。1.3 证明（1）1，如图，“线段AB和CD的长度相等”是真命题吗？通过观察，猜想结论，再动手验证2，如图，“直线a和直线b互相平行”是真命题吗？通过观察，猜想结论，再动手验证3，如图，“若∠1＝∠2，则直线a∥b”是真命题吗？
请说明理由。∵∠1=∠2（已知）， ∠2=∠3（对顶角相等）
∴∠1=∠3（等量代换）
∴a∥b（同位角相等，两直线平行）
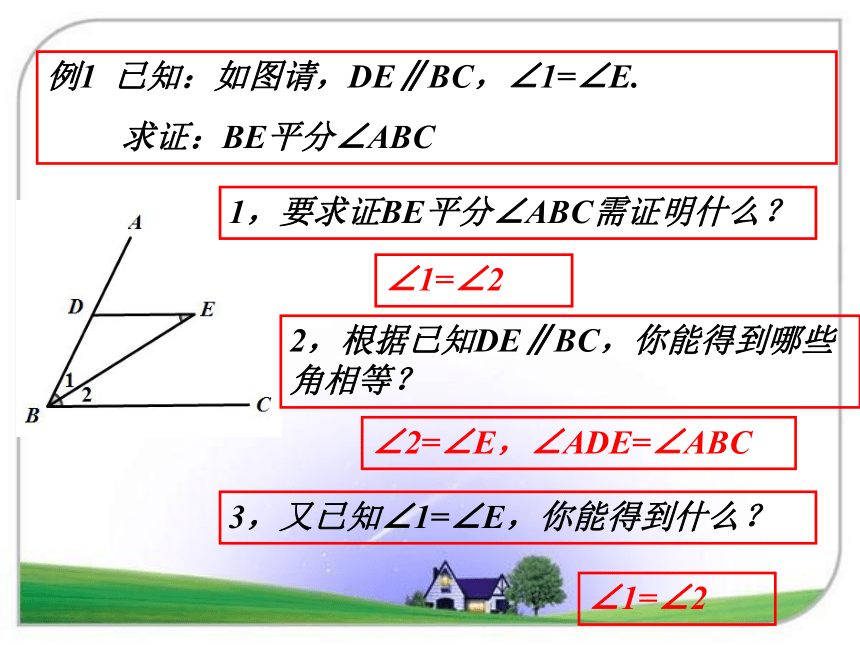
∴原命题是真命题通过上面的学习，你有何感想？ 要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、定理、推论和基本事实，一步一步推得结论成立。这样的推理过程叫做证明眼见不一定为实例1 已知：如图请，DE∥BC，∠1=∠E.
求证：BE平分∠ABC1，要求证BE平分∠ABC需证明什么？2，根据已知DE∥BC，你能得到哪些角相等？∠1=∠23，又已知∠1=∠E，你能得到什么？∠2=∠E，∠ADE=∠ABC∠1=∠2例1 已知：如图，DE∥BC，∠1=∠E.
求证：BE平分∠ABC证明：∵DE∥BC（已知）
∴∠2=∠E（ ）
又∵∠1=∠E（已知）
∴∠1=∠2（等量代换）
∴BE平分∠ABC归纳：证明∠1=∠2，是通过找到∠E来传递相等关系来完成的.
找到第三个量来传递相等关系，这是证明角相等、线段相等的常用方法之一.新课标教学网（www.xkbw.com）--海量教学资源欢迎下载！1.根据题意,画出图形;2.分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论。3.在“证明”中写出推理过程。且每一步推理都要有依据证明几何命题的一般格式：动手试一试已知：如图在△ABC中,D，E分别是AB,AC上的 点,
且∠1=∠2. 求证：∠B=∠ADE. (P17课内练习1)∵∠1=∠2（已知）
∴DE∥BC（内错角相等，两直线平行）
∴∠B=∠ADE（两直线平行，同位角相等）例2 已知：如图，AB∥CD，EP,FP分别平分
∠BEF,∠DFE
求证：∠PEF+∠PFE=90°思考： 1,已知AB∥CD，要求证∠PEF+∠PFE=90°.你会想到什么？
2,根据EP,FP是角平分线又能得到什么结论？例2变式
已知：如图,直线AB,CD被直线EF所截，EP平分∠BEF ,FP平分∠DFE ,∠PEF+∠PFE=90°
求证： AB∥CD证明：
∵EP平分∠BEF, FP平分∠DFE
∴∠BEF=2∠PEF, ∠DFE=2∠PFE
又∵ ∠PEF+∠PFE=90°
∴∠BEF+∠DEF=180°
∴AB∥CD(同旁内角互补，两直线平行)一个知识点：两个方法：①推理过程“由因倒果”一个已知条件至少能得出一个结论，证明数学日记②找第三个量传递相等关系是证明角、线段相等的常用方法之一。证明几何命题的一般格式：1.根据题意,画出图形; 2. 结合图形，在“已知”中写出条件，在“求证”中写出结论。 3.在“证明”中写出推理过程。且每一步推理都要有依据
综合法，分析法两点注意：