1.5 全等三角形的判定(1)

课件13张PPT。三角形全等的判定
SSS问题11、你能说出什么叫三角形吗？
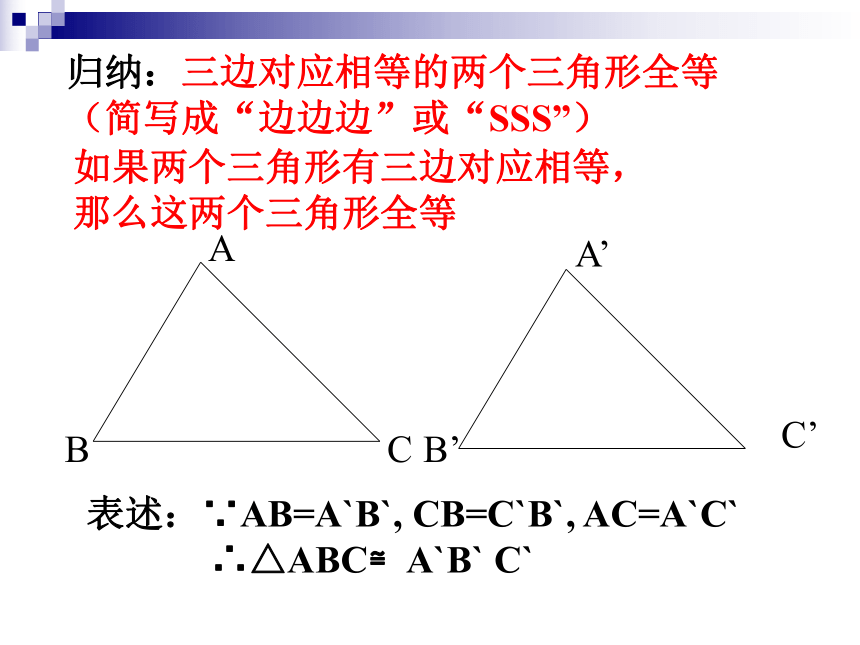
怎么样的三边能组成三角形？试一试请你用刻度尺和圆规画一个三角形，使得这个三角形的三边是7cm、4cm、5cm归纳：三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）表述：∵AB=A`B`, CB=C`B`, AC=A`C`
∴△ABC≌A`B` C`如果两个三角形有三边对应相等，
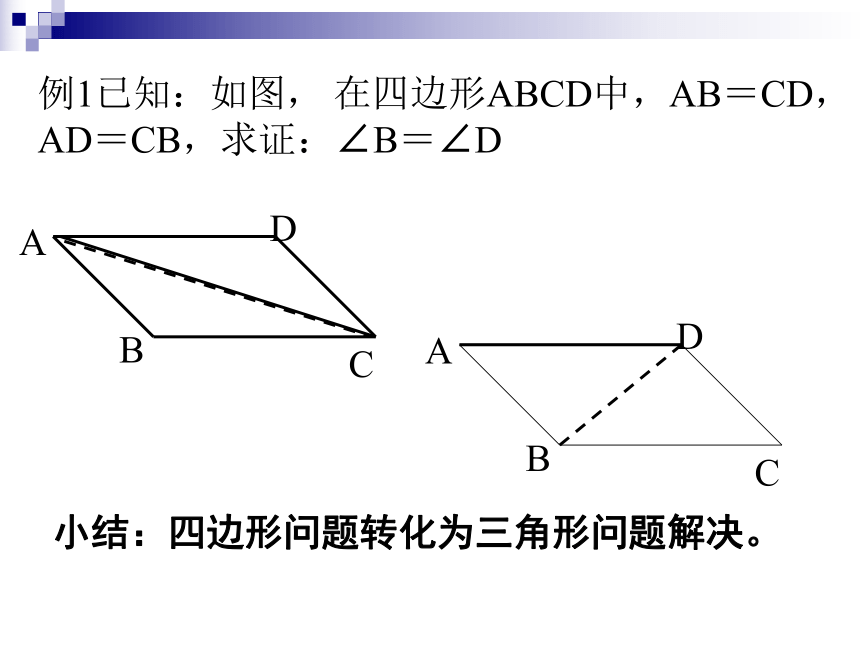
那么这两个三角形全等“边边边”公理：三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）三角形的三边长度确定，这个三角形的形状大小就完全确定，这个性质叫三角形的稳定性。这是三角形特有的性质例1已知：如图， 在四边形ABCD中，AB＝CD，AD＝CB，求证：∠B＝∠D小结：四边形问题转化为三角形问题解决。1、你能想一种方法来作一个角的平分线吗？
说说你的思路？用量角器2、已知一个角，用直尺和圆规你能作一个角的平分线吗？（1）以点A为圆心，适当长为半径做圆弧，与
角的两边分别交于E,F两点。2、分别以E，F为圆心，以 EF的长度为半径作圆弧，
两条圆弧交∠BAC内一点D3、过点A，D的射线AD就是所求作的∠BAC的平分线小明做了一个如图所示的风筝，他想去验证∠BAC与∠DAC是否相等，手头只有一把（足够长）尺子，你能帮助他想个方法吗？说明你这样做的理由。证角（或线段）相等转化为证角（或线段）所在的三角形全等4、如图,在四边形ABCD中,AB=AD,CB=CD.你能通过添加辅助线,把它分成两个全等三角形吗?若能,画出辅助线,并给出证明.
5、已知:如图,AB=DE,BC=EF,AF=DC.求证:BC∥EF.
由已知可得△ABC≌△DEF(SSS)
∴ ∠EFD＝∠BCA(全等三角形的对应角相等),
∴ ∠EFC＝∠BCA(等角的补角相等),
∴ EF∥BC(内错角相等，两直线平行).2.如图,点B,E,C,F在同一条直线上,且AB=DE,AC=DF
,BE=CF.将下面证明△ABC≌△DEF的过程补充完整.
证明:
∵ BE=CF( ),
∴ BE+EC=CF+EC,即BC=EF
.在△ABC和△DEF中,
∵
∴ △ABC≌△DEF( ).总结：2、通过证明两个三角形全等，从而可以转化证两个角和两条线段相等。3、证角（或线段）相等转化为证角（或线段）所在的三角形全等;4、四边形问题转化为三角形问题来解决。1、“SSS”公理，三角形的稳定性及其应用。