1.5全等三角形的判定（4）

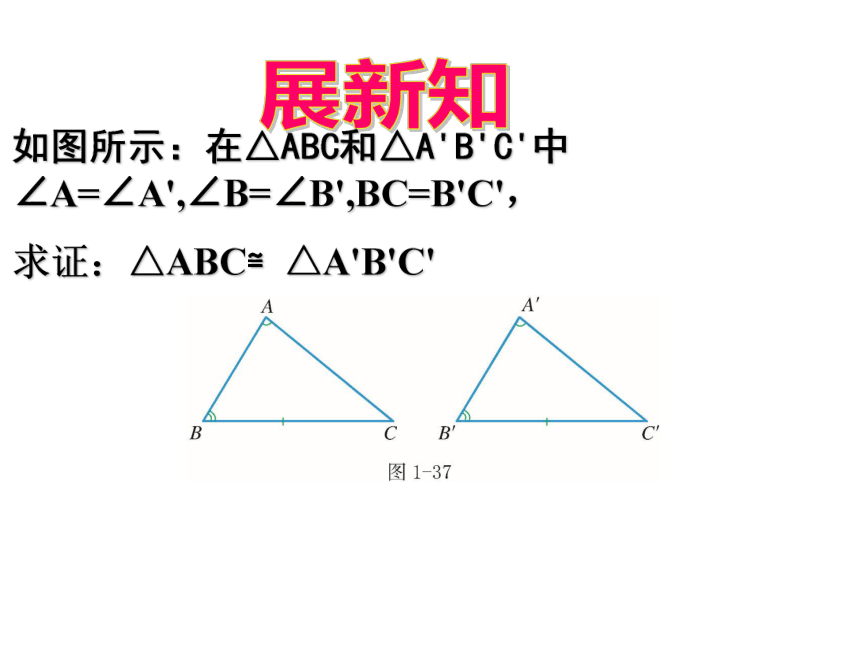
课件10张PPT。1.5 三角形全等的条件浙教版七年级 下册（第4课时）复习巩固1.我们已经学习了可以判断三角形全等有哪几种方法？SSS，SAS，ASA思考：还有没有其他方法能够判定两个三角形全等？猜想：两角及其中一个角对边对应相等的两个三角形全等展新知如图所示：在△ABC和△A'B'C'中∠A=∠A',∠B=∠B',BC=B'C'，
求证：△ABC≌△A'B'C'证明：∵∠A=∠A'，∠B=∠B'（已知）
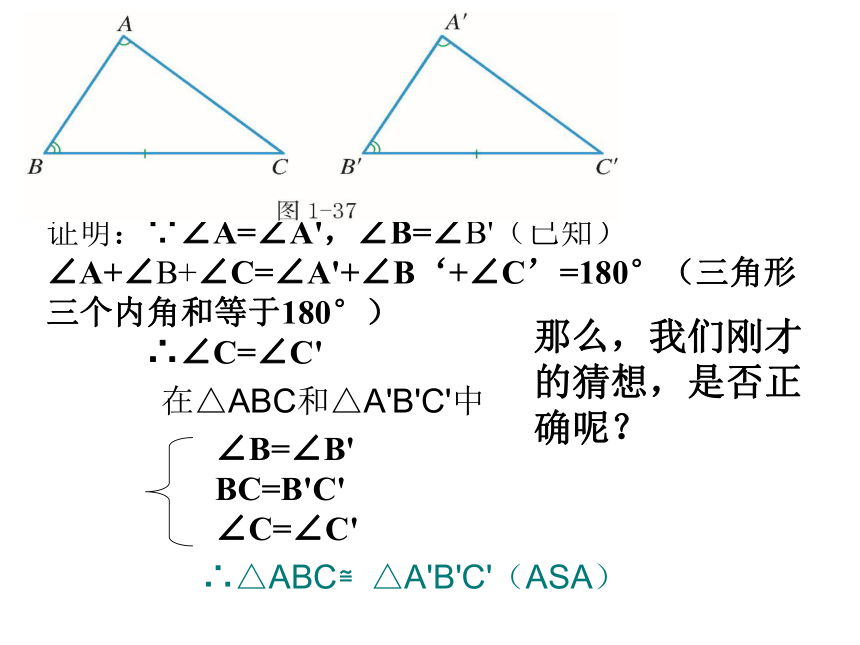
∠A+∠B+∠C=∠A'+∠B‘+∠C’=180°（三角形三个内角和等于180°）
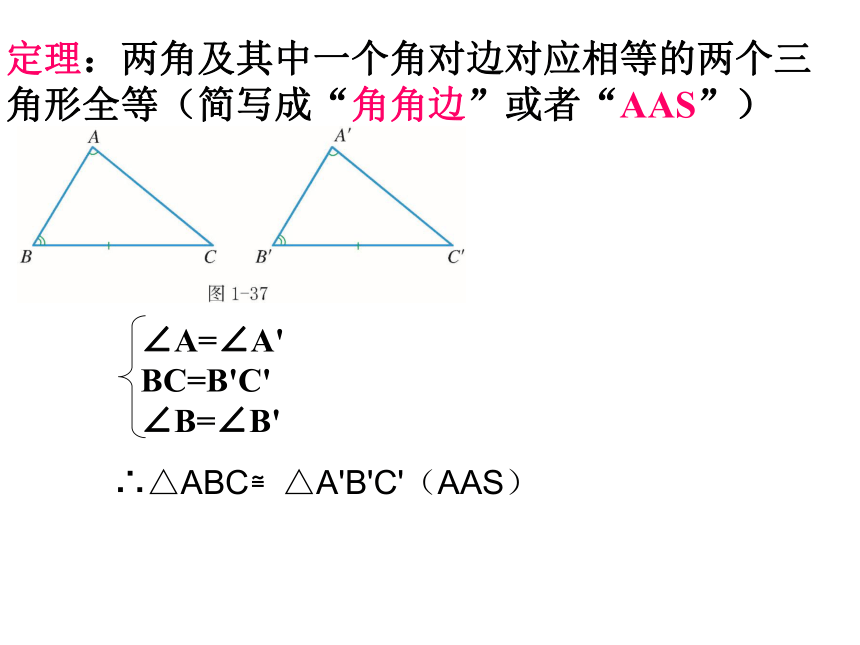
∴∠C=∠C'在△ABC和△A'B'C'中∴△ABC≌△A'B'C'（ASA）那么，我们刚才的猜想，是否正确呢？定理：两角及其中一个角对边对应相等的两个三角形全等（简写成“角角边”或者“AAS”）∴△ABC≌△A'B'C'（AAS）例6 如图，点P是∠BAC的平分线上的一点，PB⊥AB,PC⊥AC.说明PB=PC的理由.解 ∵ PB⊥AB,PC⊥AC， ∴ ∠ABP=∠ACP(垂线的意义)，在ΔABP和ΔACP中，
∠PAB=∠PAC (角平分线的意义)，
　 ∠ABP=∠ACP，
　 AP=AP(公共边)，∴ ΔABP≌ΔACP(AAS).∴ PB=PC(全等三角形的对应边相等).由此，你能否得到角平分线的一个结论？角平分线上的点到角两边的距离相等．应 用：∵P 是∠BAC的平分线上的点，
PB⊥AB,PC⊥AC，∴PB=PC(角平分线上的点到角
两边的距离相等).记一记例7、已知：如图所示，AB∥CD，PB和PC分别平分∠ABC和∠DCB，AD过点P，且与AB垂直
求证：PA=PD如图1-40，在△ABC 和△DEF中，B，E，C，F 在同一条直线上.下面给出四个论断：①AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE＝CF.
任选三个作为已知条件，余下一个作为结论，可得到几个命题？ 其中真命题有几个？ 分别给出证明.
通过本节课的学习，谈谈你的感受1、定理：两角及其中一个角对边对应相等的两个三角形全等（简写成“角角边”或者“AAS”）
2、角平分线上的点到角两边的距离相等．