2022-2023学年浙教版八年级数学上册2.6直角三角形同步达标测试题(word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册2.6直角三角形同步达标测试题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 229.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览


文档简介
2022-2023学年浙教版八年级数学上册《2.6直角三角形》同步达标测试题(附答案)
一.选择题(共7小题,满分35分)
1.已知直角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数是( )
A.50° B.45° C.40° D.30°
2.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A﹣∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=∠B=3∠C
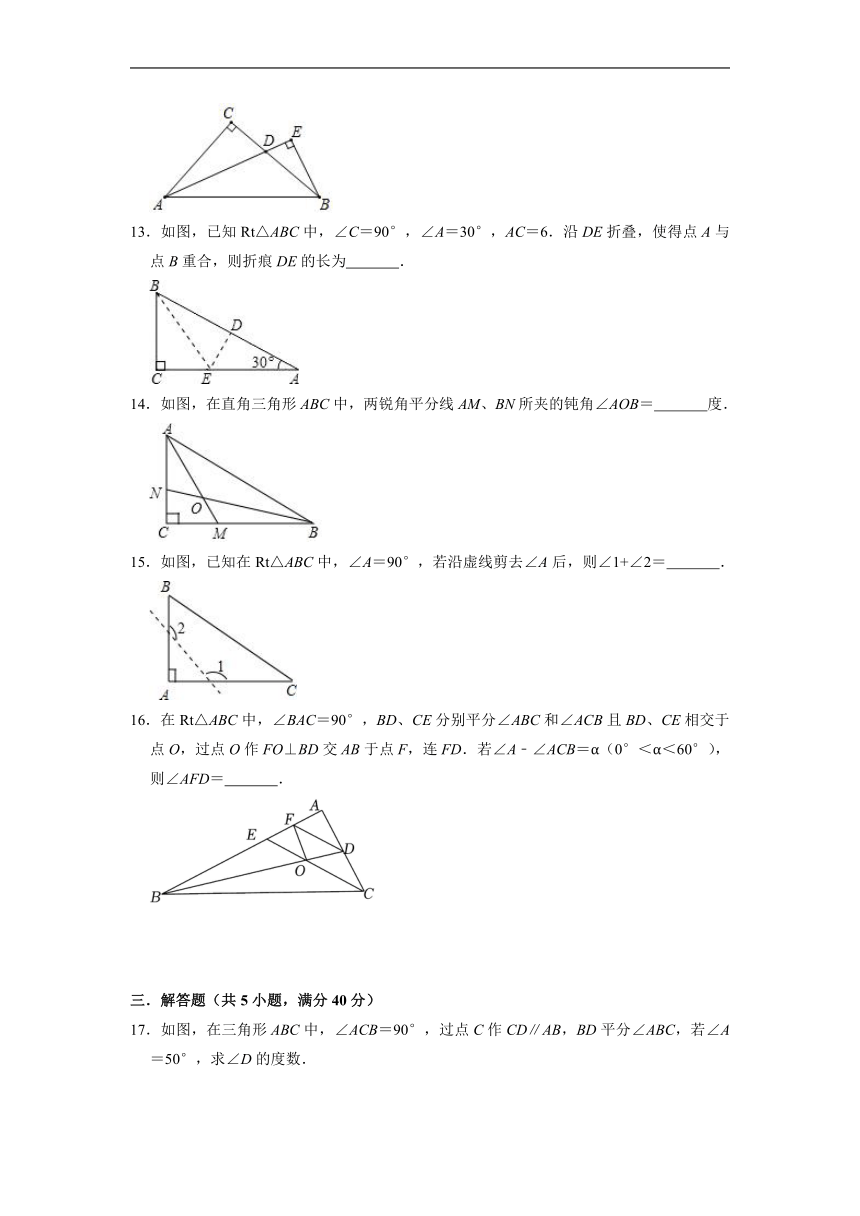
3.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
4.如图3,已知AB∥CD,现将一直角△PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.若∠PFD=32°,则∠BEP的度数为( )
A.58° B.68° C.32° D.60°
5.如图,△ABC沿直线MN折叠,使点A与AB边上的点E重合,若∠B=54°,∠C=90°,则∠ENC等于( )
A.54° B.62° C.72° D.76°
6.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
7.如图,将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)的直角顶点重合并如图叠放,当∠DEB=m°,则∠AOC=( )
A.30° B.(m﹣15)° C.(m+15)° D.m°
二.填空题(共9小题,满分45分)
8.在直角三角形中一个锐角比另一个锐角的三倍还多14度,则较大锐角的度数是 .
9.如图,已知AC⊥BC,CD⊥AB,DE⊥AC,FH⊥AB,若∠EDC=55°;则∠FHC= 度.
10.在△ABC中,高AD与BE所在直线相交于点H,且BH=AC,则∠ABC= .
11.如图,在△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则∠EDB的度数是 .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD于点E.若∠DBE=28°,则∠CAB= .
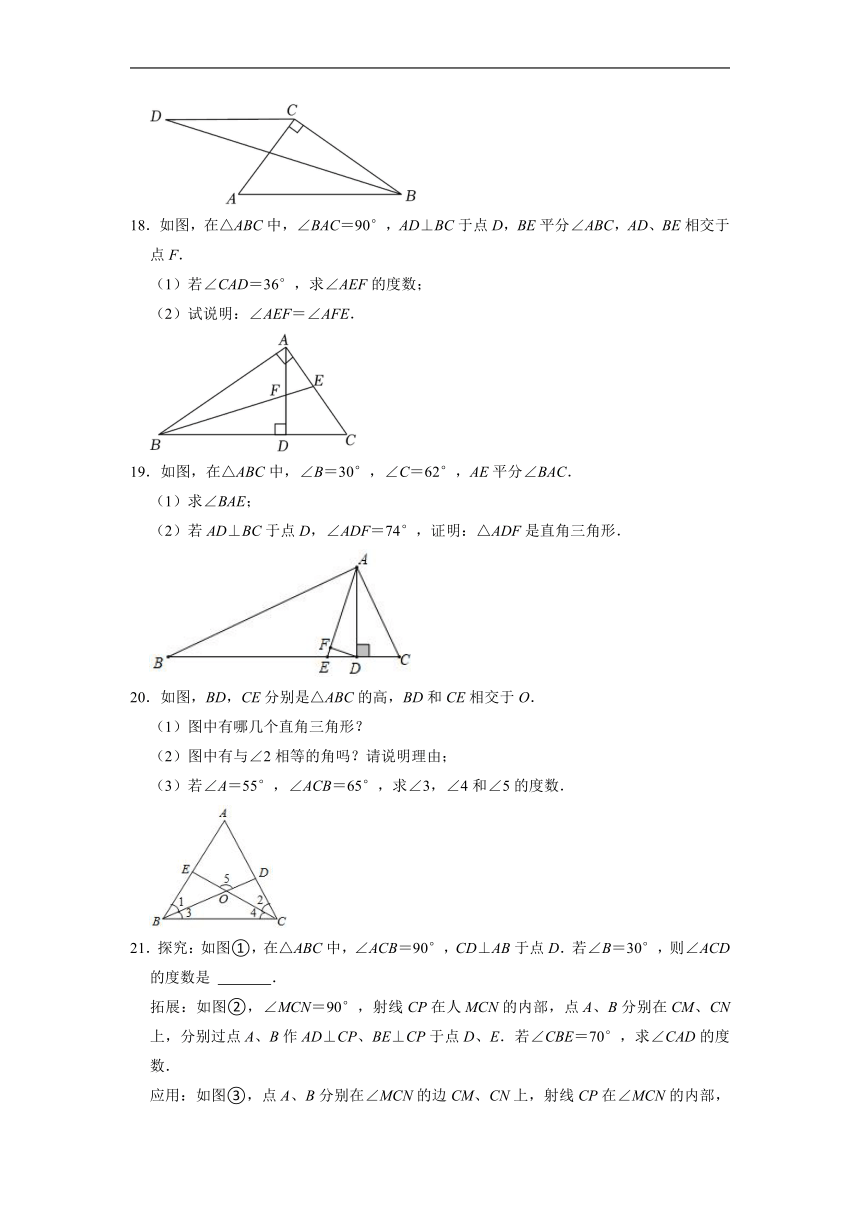
13.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为 .
14.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
15.如图,已知在Rt△ABC中,∠A=90°,若沿虚线剪去∠A后,则∠1+∠2= .
16.在Rt△ABC中,∠BAC=90°,BD、CE分别平分∠ABC和∠ACB且BD、CE相交于点O,过点O作FO⊥BD交AB于点F,连FD.若∠A﹣∠ACB=α(0°<α<60°),则∠AFD= .
三.解答题(共5小题,满分40分)
17.如图,在三角形ABC中,∠ACB=90°,过点C作CD∥AB,BD平分∠ABC,若∠A=50°,求∠D的度数.
18.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
19.如图,在△ABC中,∠B=30°,∠C=62°,AE平分∠BAC.
(1)求∠BAE;
(2)若AD⊥BC于点D,∠ADF=74°,证明:△ADF是直角三角形.
20.如图,BD,CE分别是△ABC的高,BD和CE相交于O.
(1)图中有哪几个直角三角形?
(2)图中有与∠2相等的角吗?请说明理由;
(3)若∠A=55°,∠ACB=65°,求∠3,∠4和∠5的度数.
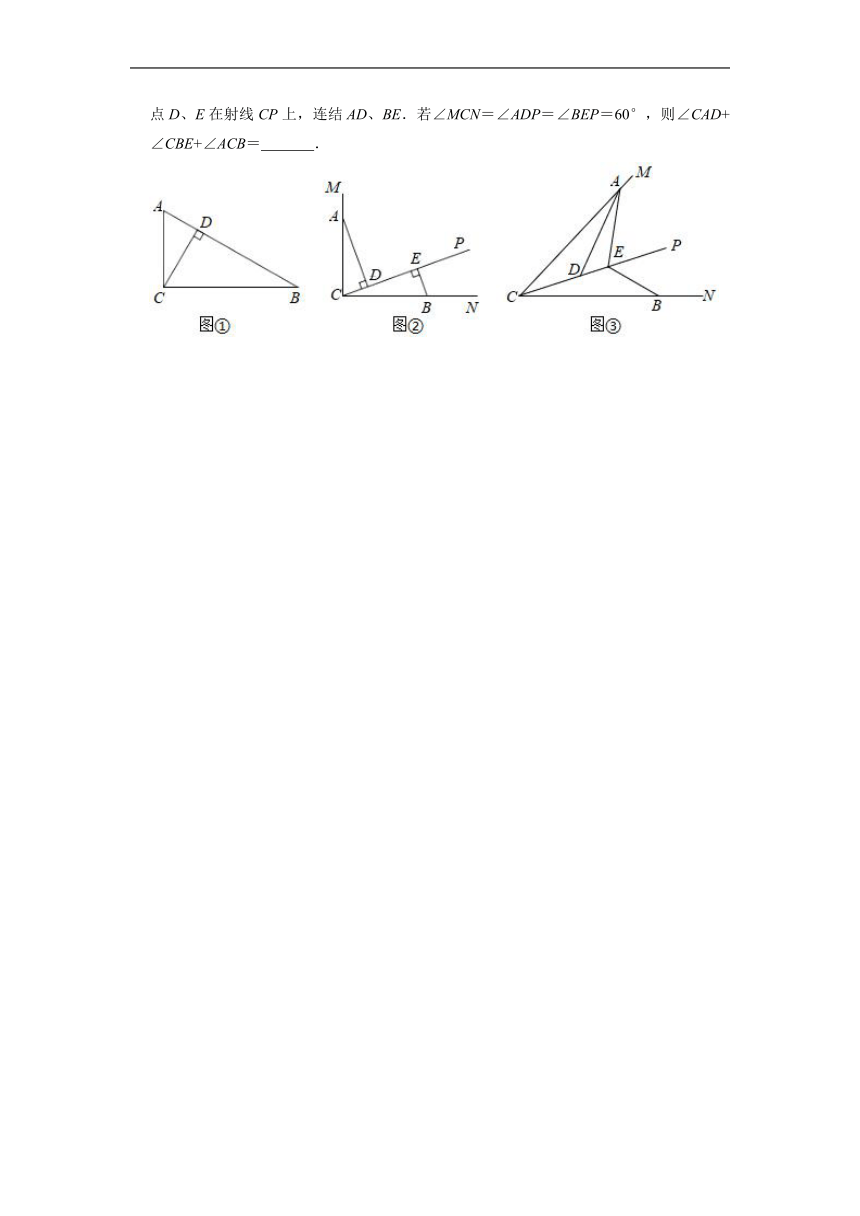
21.探究:如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D.若∠B=30°,则∠ACD的度数是 .
拓展:如图②,∠MCN=90°,射线CP在人MCN的内部,点A、B分别在CM、CN上,分别过点A、B作AD⊥CP、BE⊥CP于点D、E.若∠CBE=70°,求∠CAD的度数.
应用:如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连结AD、BE.若∠MCN=∠ADP=∠BEP=60°,则∠CAD+∠CBE+∠ACB= .
参考答案
一.选择题(共7小题,满分35分)
1.解:∵直角三角形ABC中,有一个锐角等于50°,
∴另一个锐角的度数是:90°﹣50°=40°,
故选:C.
2.解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;
B选项,∠A﹣∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;
C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;
D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.
故选:D.
3.解:如图,∵在△ABC中,∠C=60°,∠B=50°,
∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.
故选:C.
4.解:延长MP交CD于H,
∵∠MPN是△PFH的外角,
∴∠PHF=∠MPN﹣∠PFD=90°﹣32°=58°,
∵AB∥CD,
∴∠BEP=∠PHF=58°,
故选:A.
5.解:∵∠B=54°,∠C=90°,
∴∠A=90°﹣54°=36°,
由折叠的性质可知,∠NEA=∠A=36°,
∴∠ENC=∠NEA+∠A=72°,
故选:C.
6.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
7.解:∵∠DEB=m°,
∴∠AEC=∠DEB=m°,
∵∠A+∠AEC=∠C+∠AOC,∠C=45°,∠A=30°,
∴30°+m°=45°+∠AOC,
∴∠AOC=(m﹣15)°,
故选:B.
二.填空题(共9小题,满分45分)
8.解:设直角三角形较小的锐角为x,则较大的锐角为3x+14°,
则x+3x+14°=90°,
解得:x=19°,
则较大的锐角为3×19°+14°=71°,
故答案为:71°.
9.解:∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°,
∴DE∥BC,
∴∠DCB=∠EDC=55°,
∵CD⊥AB,FH⊥AB,
∴DC∥FH,
∴∠BCD+∠FHC=180°,
∴∠FHC=180°﹣55°=125°,
故答案为:125.
10.解:如图中,
∵∠BHD=∠AHE(对顶角相等),又∠AEH=∠ADC=90°,
∴∠DAC+∠C=90°,∠HAE+∠AHE=90°,
∴∠AHE=∠C(同角的余角相等),
∴∠C=∠BHD(等量代换),
∵BH=AC,∠HBD=∠DAC,∠C=∠BHD
∴△HBD≌△CAD(AAS),
∴AD=BD(全等三角形的对应边相等).
∴∠ABC=45°(等腰直角三角形的性质);
如图,当∠ABC是钝角时,同法可得AD=BD,
∴∠ABD=45°,∠ABC=135°
故答案为:45°或135°
11.解:∵△ABC中,∠ACB=90°,∠A=52°,
∴∠B=90°﹣52°=38°,
由题意可知△ACD≌△ACD,
∴∠CED=∠A=52°,
由图可知∠CED是△EBD 的外角,
∴∠CED=∠B+∠EDB,
∴52°=38°+∠EDB,
∴∠EDB=14°.
故答案为:14°.
12.解:∵BE⊥AE,
∴∠E=∠C=90°,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=28°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=56°,
故答案为56°.
13.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
14.解:∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180°﹣(∠CAM+∠NBC)=135°,
∴∠AOB=135°.
故答案为:135
15.解:∵△ADE是直角三角形,
∴∠3+∠4=90°,
∵∠2、∠1是△ADE的外角,
∴∠2=∠4+∠A,∠1=∠3+∠A,
∴∠2+∠3=2∠A+(∠4+∠3)=2×90°+90°=270°.
16.解:如图,连接AO,过O点作OM⊥AB于M,作ON⊥AC于点N,则∠FMO=∠DNO=90,
∵∠BAC=90°,∠BAC﹣∠ACB=α,
∴∠ACB=90°﹣α,∠MON=90°,
∴∠ABC=α,
∵BD平分∠ABC,
∴∠ABD=α,
∵FO⊥BD,
∴∠BOF=∠FOD=90°,
∴∠MOF=∠NOD,∠AFO=∠BOF+∠ABD=90°+α,
∵BO平分∠ABC,CO平分∠ACB,
∴AO平分∠BAC,
∴∠OAD=45°,MO=NO,
在△MOF和△NOD中,
,
∴△MOF≌△NOD(ASA),
∴OF=OD,
∴∠OFD=45°,
∴∠AFD=∠AFO﹣∠OFD=45°+α,
故答案为:45°+α.
三.解答题(共5小题,满分40分)
17.解:∵∠ACB=90°,∠A=50°,
∴∠ABC=90°﹣50°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=20°,
∵CD∥AB,
∴∠D=∠ABD=20°.
18.(1)解:∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=18°,
∴∠AEF=90°﹣∠ABE=72°;
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
19.(1)解:∵∠B=30°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣62°=88°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=×88°=44°;
(2)证明:∵AD⊥BC;
∴∠BAD=90°﹣∠B=90°﹣30°=60°,
∴∠EAD=∠BAD﹣∠BAE=60°﹣44°=16°,
∵∠ADF=74°,
∴∠ADF+∠EAD=74°+16°=90°,
∴∠AFD=90°,
∴△ADF是直角三角形.
20.解:(1)∵BD,CE分别是△ABC的高,
∴∠ADB=∠CDB=∠AEC=∠BEC=90°,
∴图中有6个直角三角形,分别为△ABD、△CBD、△ACE、△BCE、△OBE、△OCD;
(2)图中有与∠2相等的角为∠1,理由如下:
∵∠2+∠A=90°,∠1+∠A=90°,
∴∠1=∠2;
(3)∵∠CDB=90°,∠ACB=65°,
∴∠3=90°﹣∠ACB=90°﹣65°=25°,
∵∠A=55°,∠ACB=65°,
∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣55°﹣65°=60°,
∵∠BEC=90°,
∴∠4=90°﹣∠ABC=30°,
∴∠5=∠BOC=180°﹣∠3﹣∠4=180°﹣25°﹣30°=125°.
21.解:(1)在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°﹣∠A=30°;
故答案为:30°;
(2)∵BE⊥CP,
∴∠BEC=90°,
∵∠CBE=70°,
∴∠BCE=90°﹣∠CBE=20°,
∵∠ACB=90°,
∴∠ACD=90°﹣∠BCE=70°,
∵AD⊥CP,
∴∠CAD=90°﹣∠ACD=20°;
(3)∵∠ADP是△ACD的外角,
∴∠ADP=∠ACD+∠CAD=60°,
同理,∠BEP=∠BCE+∠CBE=60°,
∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE+∠BCE)=120°,
故答案为:120°.
一.选择题(共7小题,满分35分)
1.已知直角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数是( )
A.50° B.45° C.40° D.30°
2.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A﹣∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=∠B=3∠C
3.如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
A.90° B.100° C.110° D.120°
4.如图3,已知AB∥CD,现将一直角△PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.若∠PFD=32°,则∠BEP的度数为( )
A.58° B.68° C.32° D.60°
5.如图,△ABC沿直线MN折叠,使点A与AB边上的点E重合,若∠B=54°,∠C=90°,则∠ENC等于( )
A.54° B.62° C.72° D.76°
6.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
7.如图,将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)的直角顶点重合并如图叠放,当∠DEB=m°,则∠AOC=( )
A.30° B.(m﹣15)° C.(m+15)° D.m°
二.填空题(共9小题,满分45分)
8.在直角三角形中一个锐角比另一个锐角的三倍还多14度,则较大锐角的度数是 .
9.如图,已知AC⊥BC,CD⊥AB,DE⊥AC,FH⊥AB,若∠EDC=55°;则∠FHC= 度.
10.在△ABC中,高AD与BE所在直线相交于点H,且BH=AC,则∠ABC= .
11.如图,在△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则∠EDB的度数是 .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD于点E.若∠DBE=28°,则∠CAB= .
13.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为 .
14.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
15.如图,已知在Rt△ABC中,∠A=90°,若沿虚线剪去∠A后,则∠1+∠2= .
16.在Rt△ABC中,∠BAC=90°,BD、CE分别平分∠ABC和∠ACB且BD、CE相交于点O,过点O作FO⊥BD交AB于点F,连FD.若∠A﹣∠ACB=α(0°<α<60°),则∠AFD= .
三.解答题(共5小题,满分40分)
17.如图,在三角形ABC中,∠ACB=90°,过点C作CD∥AB,BD平分∠ABC,若∠A=50°,求∠D的度数.
18.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,AD、BE相交于点F.
(1)若∠CAD=36°,求∠AEF的度数;
(2)试说明:∠AEF=∠AFE.
19.如图,在△ABC中,∠B=30°,∠C=62°,AE平分∠BAC.
(1)求∠BAE;
(2)若AD⊥BC于点D,∠ADF=74°,证明:△ADF是直角三角形.
20.如图,BD,CE分别是△ABC的高,BD和CE相交于O.
(1)图中有哪几个直角三角形?
(2)图中有与∠2相等的角吗?请说明理由;
(3)若∠A=55°,∠ACB=65°,求∠3,∠4和∠5的度数.
21.探究:如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D.若∠B=30°,则∠ACD的度数是 .
拓展:如图②,∠MCN=90°,射线CP在人MCN的内部,点A、B分别在CM、CN上,分别过点A、B作AD⊥CP、BE⊥CP于点D、E.若∠CBE=70°,求∠CAD的度数.
应用:如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连结AD、BE.若∠MCN=∠ADP=∠BEP=60°,则∠CAD+∠CBE+∠ACB= .
参考答案
一.选择题(共7小题,满分35分)
1.解:∵直角三角形ABC中,有一个锐角等于50°,
∴另一个锐角的度数是:90°﹣50°=40°,
故选:C.
2.解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;
B选项,∠A﹣∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;
C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;
D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.
故选:D.
3.解:如图,∵在△ABC中,∠C=60°,∠B=50°,
∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.
故选:C.
4.解:延长MP交CD于H,
∵∠MPN是△PFH的外角,
∴∠PHF=∠MPN﹣∠PFD=90°﹣32°=58°,
∵AB∥CD,
∴∠BEP=∠PHF=58°,
故选:A.
5.解:∵∠B=54°,∠C=90°,
∴∠A=90°﹣54°=36°,
由折叠的性质可知,∠NEA=∠A=36°,
∴∠ENC=∠NEA+∠A=72°,
故选:C.
6.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
7.解:∵∠DEB=m°,
∴∠AEC=∠DEB=m°,
∵∠A+∠AEC=∠C+∠AOC,∠C=45°,∠A=30°,
∴30°+m°=45°+∠AOC,
∴∠AOC=(m﹣15)°,
故选:B.
二.填空题(共9小题,满分45分)
8.解:设直角三角形较小的锐角为x,则较大的锐角为3x+14°,
则x+3x+14°=90°,
解得:x=19°,
则较大的锐角为3×19°+14°=71°,
故答案为:71°.
9.解:∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°,
∴DE∥BC,
∴∠DCB=∠EDC=55°,
∵CD⊥AB,FH⊥AB,
∴DC∥FH,
∴∠BCD+∠FHC=180°,
∴∠FHC=180°﹣55°=125°,
故答案为:125.
10.解:如图中,
∵∠BHD=∠AHE(对顶角相等),又∠AEH=∠ADC=90°,
∴∠DAC+∠C=90°,∠HAE+∠AHE=90°,
∴∠AHE=∠C(同角的余角相等),
∴∠C=∠BHD(等量代换),
∵BH=AC,∠HBD=∠DAC,∠C=∠BHD
∴△HBD≌△CAD(AAS),
∴AD=BD(全等三角形的对应边相等).
∴∠ABC=45°(等腰直角三角形的性质);
如图,当∠ABC是钝角时,同法可得AD=BD,
∴∠ABD=45°,∠ABC=135°
故答案为:45°或135°
11.解:∵△ABC中,∠ACB=90°,∠A=52°,
∴∠B=90°﹣52°=38°,
由题意可知△ACD≌△ACD,
∴∠CED=∠A=52°,
由图可知∠CED是△EBD 的外角,
∴∠CED=∠B+∠EDB,
∴52°=38°+∠EDB,
∴∠EDB=14°.
故答案为:14°.
12.解:∵BE⊥AE,
∴∠E=∠C=90°,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=28°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=56°,
故答案为56°.
13.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
14.解:∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180°﹣(∠CAM+∠NBC)=135°,
∴∠AOB=135°.
故答案为:135
15.解:∵△ADE是直角三角形,
∴∠3+∠4=90°,
∵∠2、∠1是△ADE的外角,
∴∠2=∠4+∠A,∠1=∠3+∠A,
∴∠2+∠3=2∠A+(∠4+∠3)=2×90°+90°=270°.
16.解:如图,连接AO,过O点作OM⊥AB于M,作ON⊥AC于点N,则∠FMO=∠DNO=90,
∵∠BAC=90°,∠BAC﹣∠ACB=α,
∴∠ACB=90°﹣α,∠MON=90°,
∴∠ABC=α,
∵BD平分∠ABC,
∴∠ABD=α,
∵FO⊥BD,
∴∠BOF=∠FOD=90°,
∴∠MOF=∠NOD,∠AFO=∠BOF+∠ABD=90°+α,
∵BO平分∠ABC,CO平分∠ACB,
∴AO平分∠BAC,
∴∠OAD=45°,MO=NO,
在△MOF和△NOD中,
,
∴△MOF≌△NOD(ASA),
∴OF=OD,
∴∠OFD=45°,
∴∠AFD=∠AFO﹣∠OFD=45°+α,
故答案为:45°+α.
三.解答题(共5小题,满分40分)
17.解:∵∠ACB=90°,∠A=50°,
∴∠ABC=90°﹣50°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=20°,
∵CD∥AB,
∴∠D=∠ABD=20°.
18.(1)解:∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABD=∠CAD=36°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=18°,
∴∠AEF=90°﹣∠ABE=72°;
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
∵∠AFE=∠BFD,
∴∠AEF=∠AFE.
19.(1)解:∵∠B=30°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣62°=88°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=×88°=44°;
(2)证明:∵AD⊥BC;
∴∠BAD=90°﹣∠B=90°﹣30°=60°,
∴∠EAD=∠BAD﹣∠BAE=60°﹣44°=16°,
∵∠ADF=74°,
∴∠ADF+∠EAD=74°+16°=90°,
∴∠AFD=90°,
∴△ADF是直角三角形.
20.解:(1)∵BD,CE分别是△ABC的高,
∴∠ADB=∠CDB=∠AEC=∠BEC=90°,
∴图中有6个直角三角形,分别为△ABD、△CBD、△ACE、△BCE、△OBE、△OCD;
(2)图中有与∠2相等的角为∠1,理由如下:
∵∠2+∠A=90°,∠1+∠A=90°,
∴∠1=∠2;
(3)∵∠CDB=90°,∠ACB=65°,
∴∠3=90°﹣∠ACB=90°﹣65°=25°,
∵∠A=55°,∠ACB=65°,
∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣55°﹣65°=60°,
∵∠BEC=90°,
∴∠4=90°﹣∠ABC=30°,
∴∠5=∠BOC=180°﹣∠3﹣∠4=180°﹣25°﹣30°=125°.
21.解:(1)在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°﹣∠A=30°;
故答案为:30°;
(2)∵BE⊥CP,
∴∠BEC=90°,
∵∠CBE=70°,
∴∠BCE=90°﹣∠CBE=20°,
∵∠ACB=90°,
∴∠ACD=90°﹣∠BCE=70°,
∵AD⊥CP,
∴∠CAD=90°﹣∠ACD=20°;
(3)∵∠ADP是△ACD的外角,
∴∠ADP=∠ACD+∠CAD=60°,
同理,∠BEP=∠BCE+∠CBE=60°,
∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE+∠BCE)=120°,
故答案为:120°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
