1.5三角形全等的判定（3）

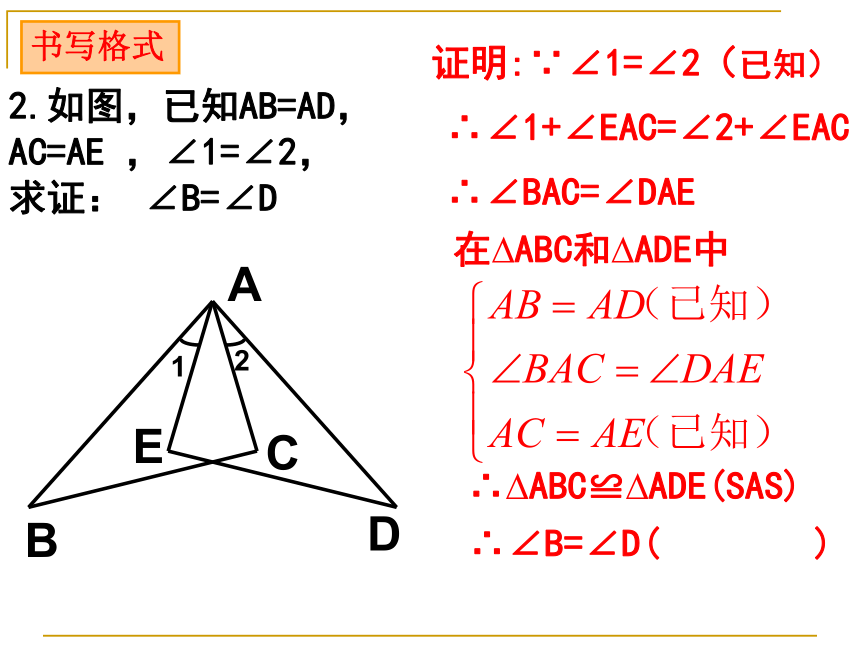
课件14张PPT。知识回顾三角形全等的判定：有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)两边及其夹角对应相等的两个三角形全等（简写成“边角边”或“SAS”）2.如图，已知AB=AD， AC=AE ，∠1=∠2，
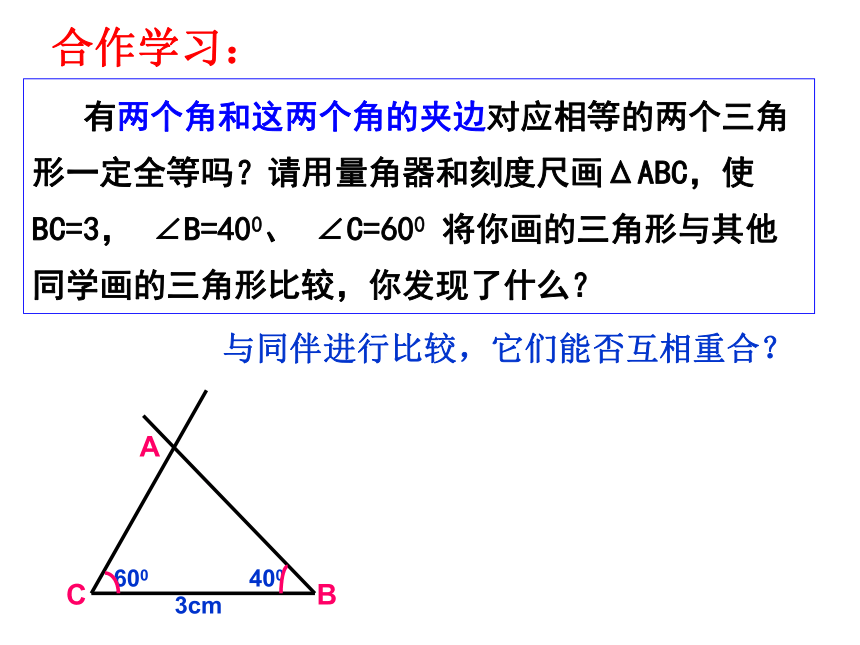
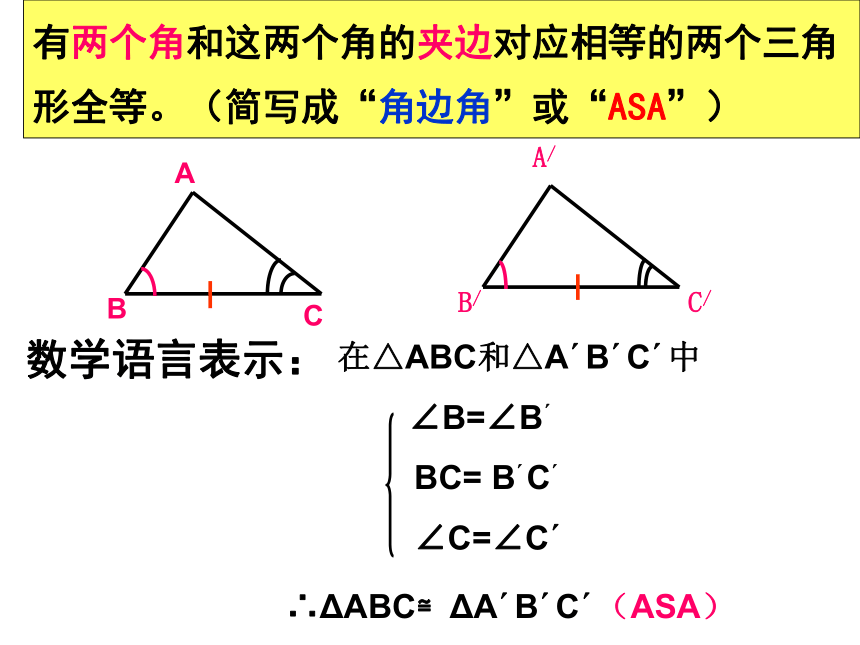
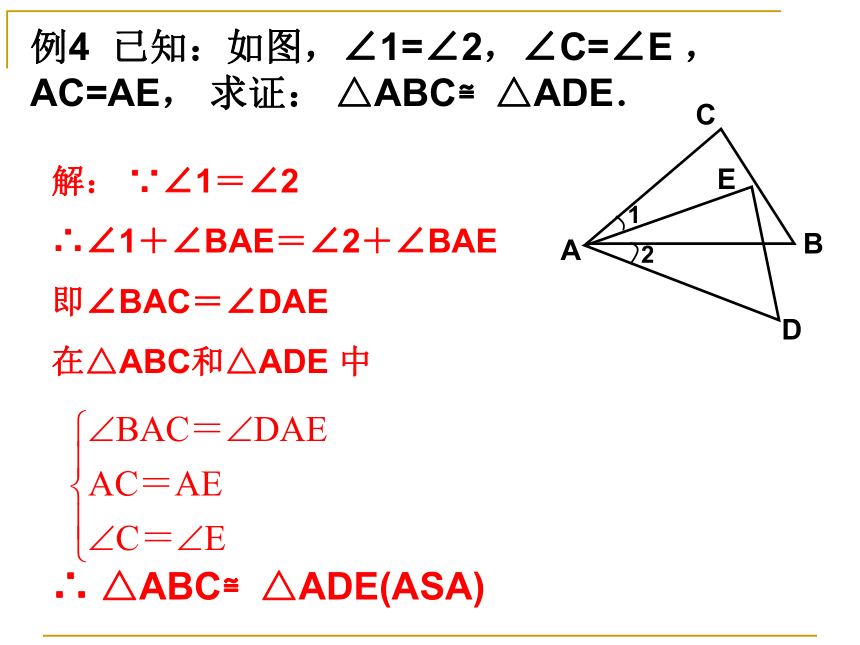
求证： ∠B=∠D证明:∵∠1=∠2（已知）∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠DAE在?ABC和?ADE中∴?ABC≌?ADE(SAS)∴∠B=∠D( )书写格式1.5三角形全等的判定（3） 有两个角和这两个角的夹边对应相等的两个三角形一定全等吗？请用量角器和刻度尺画ΔABC，使BC=3， ∠B=400、 ∠C=600 将你画的三角形与其他同学画的三角形比较，你发现了什么？CBA6004003cm与同伴进行比较，它们能否互相重合？合作学习：∴ΔABC≌ΔA′B′C′（ASA）有两个角和这两个角的夹边对应相等的两个三角形全等。（简写成“角边角”或“ASA”）数学语言表示：例4 已知：如图，∠1=∠2，∠C=∠E ，AC=AE， 求证： △ABC≌△ADE． 解： ∵∠1＝∠2　
∴∠1＋∠BAE＝∠2＋∠BAE　　　　　
即∠BAC＝∠DAE　
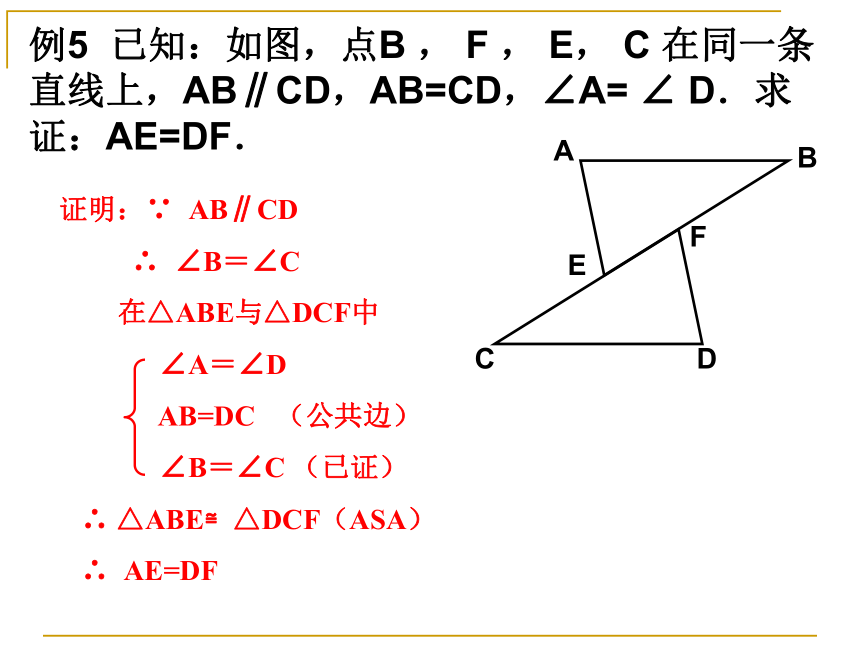
在△ABC和△ADE 中　　　　　　∴ △ABC≌△ADE(ASA)例5 已知：如图，点B ， F ， E， C 在同一条直线上，AB∥CD，AB=CD，∠A= ∠ D．求证：AE=DF．
问题思考：一块三角形玻璃被摔成三片（如图）。只需带上其中的一片，玻璃店的师傅就能重新配一块与原来相同的三角形玻璃。你知道应带哪一片碎玻璃吗？请说明理由练习.
已知: 如图,点D,E分别在AC，AB上,∠B=∠C, AB=AC.
求证:(1)AE=AD
(2)BE=CD小组讨论 1.在△ABC和△DCB中,已经存在了一个等量关系，请同学们观察一下,并写出________ ，然后小组讨论一下,如果再增加一些什么条件,就能证明这两个三角形全等,并写出其中一种证明方法.ABCDO 2.如图,有一湖的湖岸在A,B之间呈一段圆弧状,A,B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?AB—— 办法总比困难多！皮尺ABOCD 2.如图,有一湖的湖岸在A,B之间呈一段圆弧状,
A,B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A,B间的距离吗?提高题：
如图，在△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作AE的垂线CF，垂足为F，过B作BD⊥BC交CF的延长线于点D．（1）试说明：AE=CD；
（2）AC=12cm，求BD的长．解：（1）∵ AF⊥DC ∴∠AFC=900
又∵ ∠ACB=90°，
∴∠DCB+∠DCA=∠EAC+∠ACF=90°
∴∠EAC=∠DCB（同角的余角相等）
∵DB⊥BC
∴∠DBC=∠ACB=900∴△DCB≌△EAC（ASA） ∴AE=CD在△ACB和△CBD中∠DBC=∠ACB∠EAC=∠DCBAC=BC（2）由（1）得△DCB≌△EAC
∴CE=DB
∵E为BC的中点
∴小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.知识要点：（2）探索三角形全等是证明线段相等（对应边相等），
角相等（对应角相等）等问题的基本途径。数学思想：要学会用分类的思想，转化的思想解决问题。