2022-2023学年浙教版九年级数学上册 3.7 正多边形同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册 3.7 正多边形同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 08:11:04 | ||
图片预览




文档简介
浙教版九上 第3章 圆的基本性质3.7 正多边形
一、选择题(共7小题)
1. 如图所示, 是 的内接正三角形,四边形 是 的内接正方形,,则 的度数为
A. B. C. D.
2. 如图所示,边长为 的正六边形内有两个斜边长为 ,有一个角是 的直角三角形,则 的值为
A. B. C. D.
3. 如图所示,在正六边形 中, 的面积为 ,则 的面积为
A. B. C. D.
4. 蜂巢的构造非常美丽、科学.如图所示为由 个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点, 的顶点都在格点上.设定 边如图所示,若 是直角三角形,则这样的三角形有
A. 个 B. 个 C. 个 D. 个
5. 正方形 与正八边形 的边长相等,初始图形如图所示,将正方形绕点 顺时针旋转使得 与 重合,再将正方形绕点 顺时针旋转使得 与 重合 按这样的方式将正方形 旋转 次后,正方形 中与正八边形 重合的边是
A. B. C. D.
6. 阅读理解:如图1所示,在平面内选一定点 ,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点 的位置可由 的度数 与 的长度 确定,有序数对 称为点 的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系中,如果正六边形的边长为 ,有一边 在射线 上,那么正六边形的顶点 的极坐标应记为
A. B. C. D.
7. 如图所示,正六边形螺帽的边长是 ,这个扳手的开口 的值应是
A. B. C. D.
二、填空题(共7小题)
8. 如图所示,若干全等的正五边形排成环状,图中所示的是前 个五边形,要完成这一圆环还需 个五边形.
9. 如图所示,在正八边形 中,四边形 的面积为 ,则该正八边形的面积为 .
10. 如图所示,平面上有两个全等的正十边形,其中点 与点 重合,点 与点 重合.则 的度数为 .
11. 如图所示,正六边形 的边长为 ,延长 , 交于点 .以 为原点,以边 所在的直线为 轴建立平面直角坐标系,则直线 与直线 的交点坐标是 .
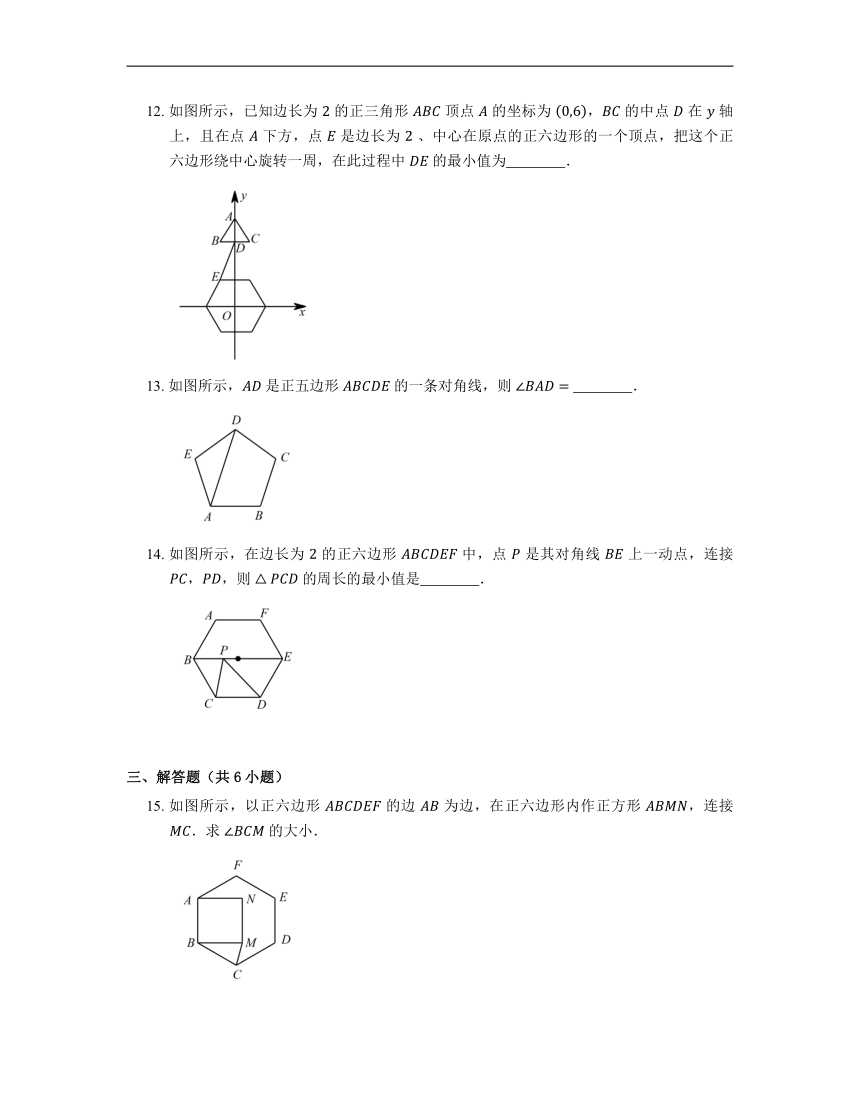
12. 如图所示,已知边长为 的正三角形 顶点 的坐标为 , 的中点 在 轴上,且在点 下方,点 是边长为 、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中 的最小值为 .
13. 如图所示, 是正五边形 的一条对角线,则 .
14. 如图所示,在边长为 的正六边形 中,点 是其对角线 上一动点,连接 ,,则 的周长的最小值是 .
三、解答题(共6小题)
15. 如图所示,以正六边形 的边 为边,在正六边形内作正方形 ,连接 .求 的大小.
16. 如图所示,已知正五边形 , 交 的延长线于点 ,交 的延长线于点 .
(1)写出图中所有的等腰三角形;
(2)求证;.
17. 如图所示,, 分别是 的内接正三角形 ,正方形 ,正五边形 ,,正 边形 的边 , 上的点,且 ,连接 ,.
(1)求图1中 的度数.
(2)图2中 的度数是 ,图3中 的度数是 .
(3)试探究 的度数与正 边形边数 的关系(直接写出答案).
18. 如图所示, 是正八边形 的一条对角线.
(1)在剩余的顶点 ,,,,, 中,连接两个顶点,使连接的线段与 平行,并说明理由.
(2)两边延长 ,,,,使延长线分别交于点 ,,,,若 ,求四边形 的面积.
19. 如图所示,正三角形、正方形、正六边形等正 边形与圆的形状有差异,我们将正 边形与圆的接近程度称为“接近度”.
(1)按角定义:设正 边形的每个内角的度数为 ,将正 边形的“接近度”定义为 , 越小,该正 边形就越接近于圆.
①若 ,则该正 边形的“接近度”等于 .
②若 ,则该正 边形的“接近度”等于 .
③当“接近度”等于 时正 边形就成了圆.
(2)按边定义:设一个正 边形的外接圆的半径为 ,正 边形的中心到各边的距离为 ,将正 边形的“接近度”定义为 .请分别计算 , 时正 边型的“接近度”,并猜测当“接近度”等于多少时,正 边形就成了圆.
20. (1)如图 1 所示, 是 的内接等边三角形,点 为 上一动点,求证:.
(2)如图 2 所示,四边形 是 的内接正方形,点 为 上一动点,求证:.
(3)如图 3 所示,六边形 是 的内接正六边形,点 为 上一动点,请探究 ,, 三者之间有何数量关系,并给予证明.
答案
1. C
2. C
3. C
4. D
5. D
6. A
7. A
8.
9.
10.
11.
12.
13.
【解析】
设 是正五边形的中心,连接 ,.
则 ,
.
14.
【解析】要使 的周长最小,即 最小.利用正多边形的性质可得点 关于 的对称点为点 ,连接 交 于点 ,
那么有 , 最小.又易知四边形 为等腰梯形,,则作 于点 , 于点 .
,
,
,从而 ,故 的周长的最小值为 .
15. 六边形 为正六边形,
,.
四边形 为正方形,
,.
,.
.
16. (1) 等腰三角形有:,,,.
(2) 五边形 是正五边形,
,,
,,
,
,
.
17. (1) 连接 ,.
,
.
,点 是外接圆的圆心,
平分 , 平分 .
.
,,
.
.
.
,
.
.
(2) ;
(3)
18. (1) 如图所示,连接 ,.
理由如下: 八边形 是正八边形,
它的内角都为 .
,
.
.
正八边形 关于直线 对称,
.
.
.
(2) 由题意可知 ,
,
同理可得 .
四边形 是矩形.
,,
.
.
.
四边形 是正方形.
在 中,
,,
.
.
.
19. (1) ① ;② ;③
(2) 如图1所示,
当 时,
,
.
.
.
如图2所示,
当 时,
,
.
.
.
当“接近度”等于 时,正 边形就成了圆.
20. (1) 如图 1 所示,延长 至点 ,使 ,连接 ,
,,, 四点共圆,
.
,
.
,
是等边三角形.
,.
,,
,
, 为等边三角形,
,.
.
.
(2) 如图 2 所示,过点 作 交 于点 .
,
.
,
,.
,
.
.
.
(3) .
证明:如图 3 所示,过点 作 于点 ,在 止截取 ,连接 .
,,
.
.
.
,
.
.
.
一、选择题(共7小题)
1. 如图所示, 是 的内接正三角形,四边形 是 的内接正方形,,则 的度数为
A. B. C. D.
2. 如图所示,边长为 的正六边形内有两个斜边长为 ,有一个角是 的直角三角形,则 的值为
A. B. C. D.
3. 如图所示,在正六边形 中, 的面积为 ,则 的面积为
A. B. C. D.
4. 蜂巢的构造非常美丽、科学.如图所示为由 个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点, 的顶点都在格点上.设定 边如图所示,若 是直角三角形,则这样的三角形有
A. 个 B. 个 C. 个 D. 个
5. 正方形 与正八边形 的边长相等,初始图形如图所示,将正方形绕点 顺时针旋转使得 与 重合,再将正方形绕点 顺时针旋转使得 与 重合 按这样的方式将正方形 旋转 次后,正方形 中与正八边形 重合的边是
A. B. C. D.
6. 阅读理解:如图1所示,在平面内选一定点 ,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点 的位置可由 的度数 与 的长度 确定,有序数对 称为点 的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系中,如果正六边形的边长为 ,有一边 在射线 上,那么正六边形的顶点 的极坐标应记为
A. B. C. D.
7. 如图所示,正六边形螺帽的边长是 ,这个扳手的开口 的值应是
A. B. C. D.
二、填空题(共7小题)
8. 如图所示,若干全等的正五边形排成环状,图中所示的是前 个五边形,要完成这一圆环还需 个五边形.
9. 如图所示,在正八边形 中,四边形 的面积为 ,则该正八边形的面积为 .
10. 如图所示,平面上有两个全等的正十边形,其中点 与点 重合,点 与点 重合.则 的度数为 .
11. 如图所示,正六边形 的边长为 ,延长 , 交于点 .以 为原点,以边 所在的直线为 轴建立平面直角坐标系,则直线 与直线 的交点坐标是 .
12. 如图所示,已知边长为 的正三角形 顶点 的坐标为 , 的中点 在 轴上,且在点 下方,点 是边长为 、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中 的最小值为 .
13. 如图所示, 是正五边形 的一条对角线,则 .
14. 如图所示,在边长为 的正六边形 中,点 是其对角线 上一动点,连接 ,,则 的周长的最小值是 .
三、解答题(共6小题)
15. 如图所示,以正六边形 的边 为边,在正六边形内作正方形 ,连接 .求 的大小.
16. 如图所示,已知正五边形 , 交 的延长线于点 ,交 的延长线于点 .
(1)写出图中所有的等腰三角形;
(2)求证;.
17. 如图所示,, 分别是 的内接正三角形 ,正方形 ,正五边形 ,,正 边形 的边 , 上的点,且 ,连接 ,.
(1)求图1中 的度数.
(2)图2中 的度数是 ,图3中 的度数是 .
(3)试探究 的度数与正 边形边数 的关系(直接写出答案).
18. 如图所示, 是正八边形 的一条对角线.
(1)在剩余的顶点 ,,,,, 中,连接两个顶点,使连接的线段与 平行,并说明理由.
(2)两边延长 ,,,,使延长线分别交于点 ,,,,若 ,求四边形 的面积.
19. 如图所示,正三角形、正方形、正六边形等正 边形与圆的形状有差异,我们将正 边形与圆的接近程度称为“接近度”.
(1)按角定义:设正 边形的每个内角的度数为 ,将正 边形的“接近度”定义为 , 越小,该正 边形就越接近于圆.
①若 ,则该正 边形的“接近度”等于 .
②若 ,则该正 边形的“接近度”等于 .
③当“接近度”等于 时正 边形就成了圆.
(2)按边定义:设一个正 边形的外接圆的半径为 ,正 边形的中心到各边的距离为 ,将正 边形的“接近度”定义为 .请分别计算 , 时正 边型的“接近度”,并猜测当“接近度”等于多少时,正 边形就成了圆.
20. (1)如图 1 所示, 是 的内接等边三角形,点 为 上一动点,求证:.
(2)如图 2 所示,四边形 是 的内接正方形,点 为 上一动点,求证:.
(3)如图 3 所示,六边形 是 的内接正六边形,点 为 上一动点,请探究 ,, 三者之间有何数量关系,并给予证明.
答案
1. C
2. C
3. C
4. D
5. D
6. A
7. A
8.
9.
10.
11.
12.
13.
【解析】
设 是正五边形的中心,连接 ,.
则 ,
.
14.
【解析】要使 的周长最小,即 最小.利用正多边形的性质可得点 关于 的对称点为点 ,连接 交 于点 ,
那么有 , 最小.又易知四边形 为等腰梯形,,则作 于点 , 于点 .
,
,
,从而 ,故 的周长的最小值为 .
15. 六边形 为正六边形,
,.
四边形 为正方形,
,.
,.
.
16. (1) 等腰三角形有:,,,.
(2) 五边形 是正五边形,
,,
,,
,
,
.
17. (1) 连接 ,.
,
.
,点 是外接圆的圆心,
平分 , 平分 .
.
,,
.
.
.
,
.
.
(2) ;
(3)
18. (1) 如图所示,连接 ,.
理由如下: 八边形 是正八边形,
它的内角都为 .
,
.
.
正八边形 关于直线 对称,
.
.
.
(2) 由题意可知 ,
,
同理可得 .
四边形 是矩形.
,,
.
.
.
四边形 是正方形.
在 中,
,,
.
.
.
19. (1) ① ;② ;③
(2) 如图1所示,
当 时,
,
.
.
.
如图2所示,
当 时,
,
.
.
.
当“接近度”等于 时,正 边形就成了圆.
20. (1) 如图 1 所示,延长 至点 ,使 ,连接 ,
,,, 四点共圆,
.
,
.
,
是等边三角形.
,.
,,
,
, 为等边三角形,
,.
.
.
(2) 如图 2 所示,过点 作 交 于点 .
,
.
,
,.
,
.
.
.
(3) .
证明:如图 3 所示,过点 作 于点 ,在 止截取 ,连接 .
,,
.
.
.
,
.
.
.
同课章节目录
