2022-2023学年浙教版九年级数学上册3.8 弧长及扇形的面积同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册3.8 弧长及扇形的面积同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 08:07:02 | ||
图片预览


文档简介
浙教版九上 第3章 圆的基本性质3.8 弧长及扇形的面积
一、选择题(共9小题)
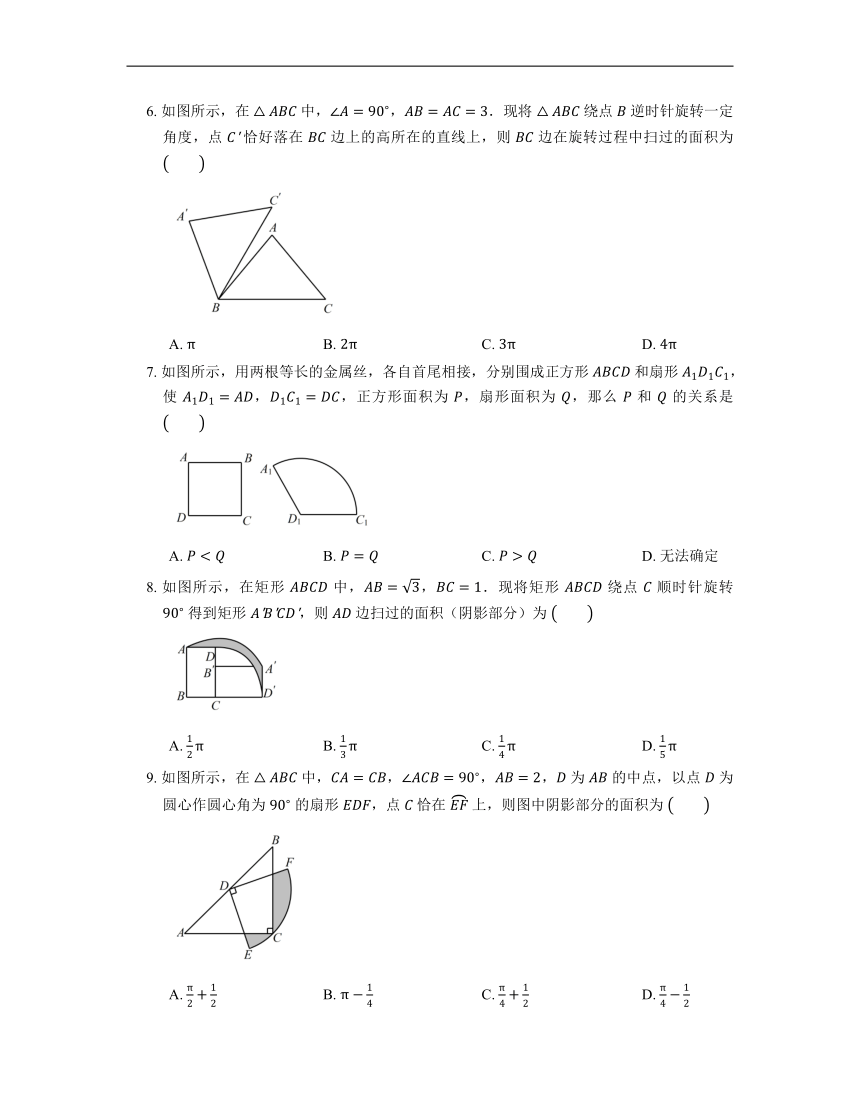
1. 挂钟分针长 ,经过 ,它扫过的面积为
A. B. C. D.
2. 如图所示,三个小正方形的边长都为 ,则图中阴影部分面积的和是
A. B. C. D.
3. 如图,在正方形 中,对角线 的长为 .若将 绕点 旋转后,点 落在 延长线上的点 处,点 经过的路径为 ,则图中阴影部分的面积是
A. B. C. D.
4. 如图所示,在 中,,,分别以 , 为直径作半圆,则图中阴影部分面积是
A. B. C. D.
5. 如图所示,将含 角的直角三角尺 绕顶点 顺时针旋转 后得到 ,点 经过的路径为 ,若 ,,则图中阴影部分的面积是
A. B. C. D.
6. 如图所示,在 中,,.现将 绕点 逆时针旋转一定角度,点 恰好落在 边上的高所在的直线上,则 边在旋转过程中扫过的面积为
A. B. C. D.
7. 如图所示,用两根等长的金属丝,各自首尾相接,分别围成正方形 和扇形 ,使 ,,正方形面积为 ,扇形面积为 ,那么 和 的关系是
A. B. C. D. 无法确定
8. 如图所示,在矩形 中,,.现将矩形 绕点 顺时针旋转 得到矩形 ,则 边扫过的面积(阴影部分)为
A. B. C. D.
9. 如图所示,在 中,,,, 为 的中点,以点 为圆心作圆心角为 的扇形 ,点 恰在 上,则图中阴影部分的面积为
A. B. C. D.
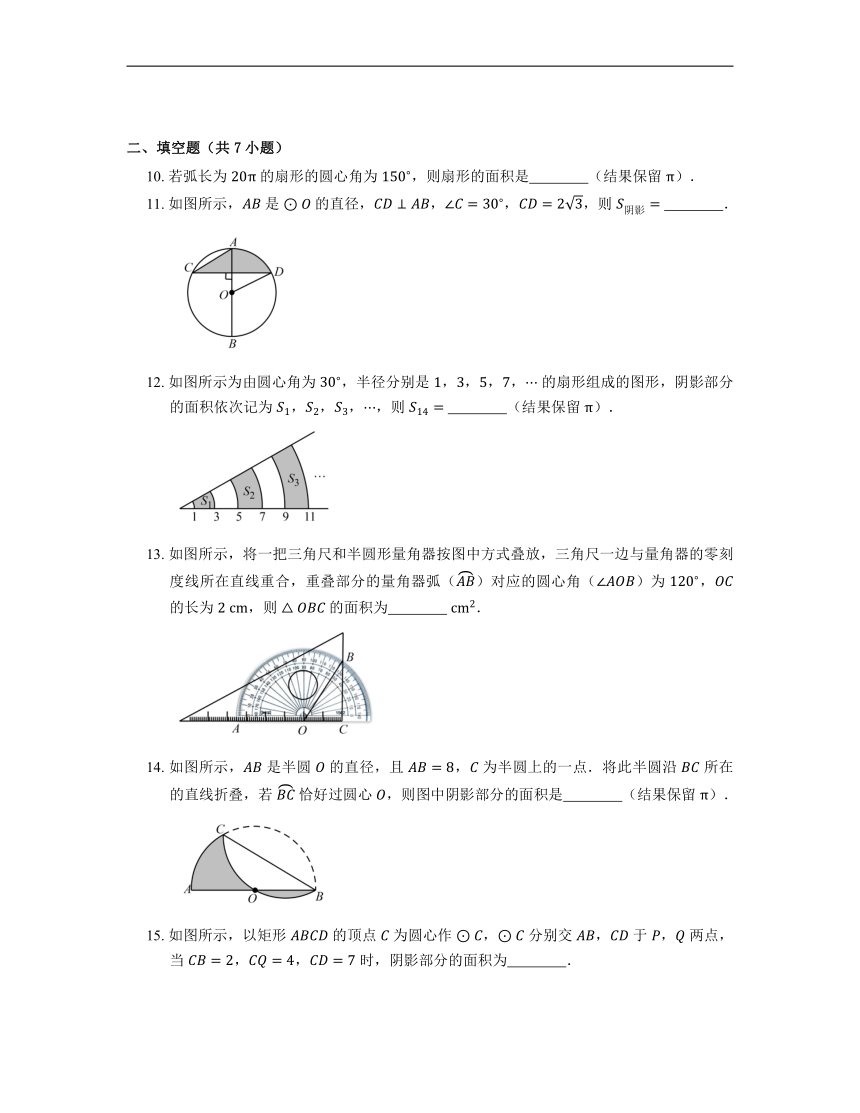
二、填空题(共7小题)
10. 若弧长为 的扇形的圆心角为 ,则扇形的面积是 (结果保留 ).
11. 如图所示, 是 的直径,,,,则 .
12. 如图所示为由圆心角为 ,半径分别是 ,,,, 的扇形组成的图形,阴影部分的面积依次记为 ,,,,则 (结果保留 ).
13. 如图所示,将一把三角尺和半圆形量角器按图中方式叠放,三角尺一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角()为 , 的长为 ,则 的面积为 .
14. 如图所示, 是半圆 的直径,且 , 为半圆上的一点.将此半圆沿 所在的直线折叠,若 恰好过圆心 ,则图中阴影部分的面积是 (结果保留 ).
15. 如图所示,以矩形 的顶点 为圆心作 , 分别交 , 于 , 两点,当 ,, 时,阴影部分的面积为 .
16. 如图所示,在扇形 中,.扇形半径为 ,点 在 上,,垂足为点 ,当 的面积最大时,图中阴影部分的面积为 .
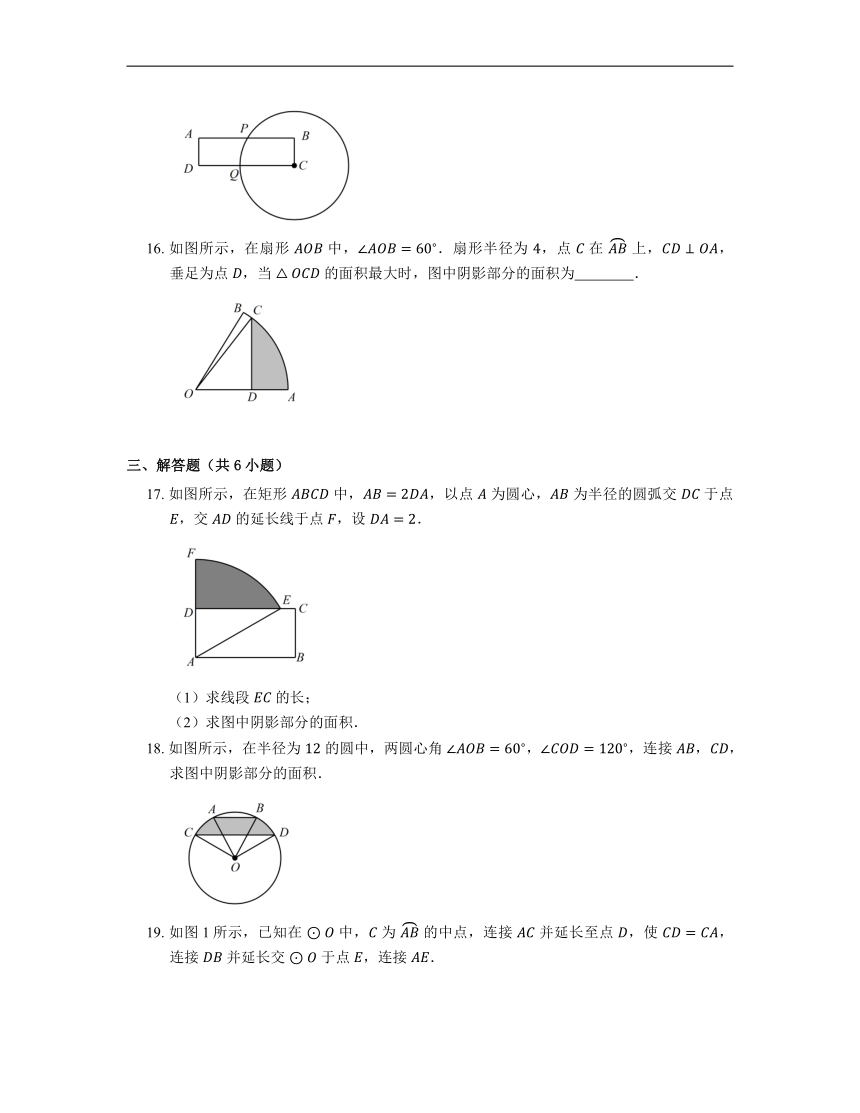
三、解答题(共6小题)
17. 如图所示,在矩形 中,,以点 为圆心, 为半径的圆弧交 于点 ,交 的延长线于点 ,设 .
(1)求线段 的长;
(2)求图中阴影部分的面积.
18. 如图所示,在半径为 的圆中,两圆心角 ,,连接 ,,求图中阴影部分的面积.
19. 如图1所示,已知在 中, 为 的中点,连接 并延长至点 ,使 ,连接 并延长交 于点 ,连接 .
(1)求证: 是 的直径.
(2)如图2所示,连接 , 半径为 , 的长为 ,求阴影部分的面积之和(结果保留 与根号).
20. 如图所示,在矩形 中,,,将一块直径为 的半圆形纸片放置在矩形 中,使其直径于 重合,现将半圆绕点 顺时针旋转至 处,半圆弧 与 交于点 ,设 .
(1)若 ,求 的度数.
(2)当 时,求阴影部分的面积.
21. 已知点 是正方形 内的一点,连 ,,.
(1)将 绕点 顺时针旋转 到 的位置(如图 1 所示).
①设 的长为 , 的长为 ,求 旋转到 的过程中边 所扫过区域(图中阴影部分)的面积.
②若 ,,,求 的长.
(2)如图 2 所示,若 ,请说明点 必在对角线 上.
22. 如图所示, 是半圆 的直径,弦 ,弦 ,连接 ,,求图中阴影部分的面积.
答案
1. A
2. B
3. C
4. D
5. A
6. C
7. B
8. C
9. D
10.
11.
12.
13.
14.
15.
16.
17. (1) 因为在矩形 中,,,
所以 .
所以 .
所以 .
(2) 因为 ,
所以 ,
所以 ,
所以图中阴影部分的面积为:.
18. ,,则 ,,,则 ,
.
19. (1) 如图所示,连接 ,.
为 的中点,
.
,
.
,.
.
.
是 的直径.
(2) 是 的直径,
.
,,
.
.
20. (1) 如图所示,连接 .
是直径,
.
,,
.
.
.
(2) 如图所示,连接 .
21. (1) ①
②如图 1 所示,连接 .
,,
.
,,
,
即 ,, 三点共线,.
在 中,,,
.
(2) 如图 2 所示,将 绕点 顺时针旋转 到 的位置,连接 .
,.
.
,
.
.
,
.
,
.
,, 三点共线,即点 在对角线 上.
22. ,,
是 的中点, 是 的中点.
.
如图所示,过点 作 于点 , 于点 ,
则 ,,,
.
过点 作 ,交 于点 ,则 ,
.
为等腰三角形.
.
过点 作 于点 ,则 .
在等腰三角形 中,,
.
在 中,.
.
一、选择题(共9小题)
1. 挂钟分针长 ,经过 ,它扫过的面积为
A. B. C. D.
2. 如图所示,三个小正方形的边长都为 ,则图中阴影部分面积的和是
A. B. C. D.
3. 如图,在正方形 中,对角线 的长为 .若将 绕点 旋转后,点 落在 延长线上的点 处,点 经过的路径为 ,则图中阴影部分的面积是
A. B. C. D.
4. 如图所示,在 中,,,分别以 , 为直径作半圆,则图中阴影部分面积是
A. B. C. D.
5. 如图所示,将含 角的直角三角尺 绕顶点 顺时针旋转 后得到 ,点 经过的路径为 ,若 ,,则图中阴影部分的面积是
A. B. C. D.
6. 如图所示,在 中,,.现将 绕点 逆时针旋转一定角度,点 恰好落在 边上的高所在的直线上,则 边在旋转过程中扫过的面积为
A. B. C. D.
7. 如图所示,用两根等长的金属丝,各自首尾相接,分别围成正方形 和扇形 ,使 ,,正方形面积为 ,扇形面积为 ,那么 和 的关系是
A. B. C. D. 无法确定
8. 如图所示,在矩形 中,,.现将矩形 绕点 顺时针旋转 得到矩形 ,则 边扫过的面积(阴影部分)为
A. B. C. D.
9. 如图所示,在 中,,,, 为 的中点,以点 为圆心作圆心角为 的扇形 ,点 恰在 上,则图中阴影部分的面积为
A. B. C. D.
二、填空题(共7小题)
10. 若弧长为 的扇形的圆心角为 ,则扇形的面积是 (结果保留 ).
11. 如图所示, 是 的直径,,,,则 .
12. 如图所示为由圆心角为 ,半径分别是 ,,,, 的扇形组成的图形,阴影部分的面积依次记为 ,,,,则 (结果保留 ).
13. 如图所示,将一把三角尺和半圆形量角器按图中方式叠放,三角尺一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角()为 , 的长为 ,则 的面积为 .
14. 如图所示, 是半圆 的直径,且 , 为半圆上的一点.将此半圆沿 所在的直线折叠,若 恰好过圆心 ,则图中阴影部分的面积是 (结果保留 ).
15. 如图所示,以矩形 的顶点 为圆心作 , 分别交 , 于 , 两点,当 ,, 时,阴影部分的面积为 .
16. 如图所示,在扇形 中,.扇形半径为 ,点 在 上,,垂足为点 ,当 的面积最大时,图中阴影部分的面积为 .
三、解答题(共6小题)
17. 如图所示,在矩形 中,,以点 为圆心, 为半径的圆弧交 于点 ,交 的延长线于点 ,设 .
(1)求线段 的长;
(2)求图中阴影部分的面积.
18. 如图所示,在半径为 的圆中,两圆心角 ,,连接 ,,求图中阴影部分的面积.
19. 如图1所示,已知在 中, 为 的中点,连接 并延长至点 ,使 ,连接 并延长交 于点 ,连接 .
(1)求证: 是 的直径.
(2)如图2所示,连接 , 半径为 , 的长为 ,求阴影部分的面积之和(结果保留 与根号).
20. 如图所示,在矩形 中,,,将一块直径为 的半圆形纸片放置在矩形 中,使其直径于 重合,现将半圆绕点 顺时针旋转至 处,半圆弧 与 交于点 ,设 .
(1)若 ,求 的度数.
(2)当 时,求阴影部分的面积.
21. 已知点 是正方形 内的一点,连 ,,.
(1)将 绕点 顺时针旋转 到 的位置(如图 1 所示).
①设 的长为 , 的长为 ,求 旋转到 的过程中边 所扫过区域(图中阴影部分)的面积.
②若 ,,,求 的长.
(2)如图 2 所示,若 ,请说明点 必在对角线 上.
22. 如图所示, 是半圆 的直径,弦 ,弦 ,连接 ,,求图中阴影部分的面积.
答案
1. A
2. B
3. C
4. D
5. A
6. C
7. B
8. C
9. D
10.
11.
12.
13.
14.
15.
16.
17. (1) 因为在矩形 中,,,
所以 .
所以 .
所以 .
(2) 因为 ,
所以 ,
所以 ,
所以图中阴影部分的面积为:.
18. ,,则 ,,,则 ,
.
19. (1) 如图所示,连接 ,.
为 的中点,
.
,
.
,.
.
.
是 的直径.
(2) 是 的直径,
.
,,
.
.
20. (1) 如图所示,连接 .
是直径,
.
,,
.
.
.
(2) 如图所示,连接 .
21. (1) ①
②如图 1 所示,连接 .
,,
.
,,
,
即 ,, 三点共线,.
在 中,,,
.
(2) 如图 2 所示,将 绕点 顺时针旋转 到 的位置,连接 .
,.
.
,
.
.
,
.
,
.
,, 三点共线,即点 在对角线 上.
22. ,,
是 的中点, 是 的中点.
.
如图所示,过点 作 于点 , 于点 ,
则 ,,,
.
过点 作 ,交 于点 ,则 ,
.
为等腰三角形.
.
过点 作 于点 ,则 .
在等腰三角形 中,,
.
在 中,.
.
同课章节目录
