2022-2023学年浙教版九年级数学上册 3.3 垂径定理 同步练习(word版 含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册 3.3 垂径定理 同步练习(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 15:31:39 | ||
图片预览



文档简介
浙教版九上 第3章 圆的基本性质3.3 垂径定理
一、选择题(共9小题)
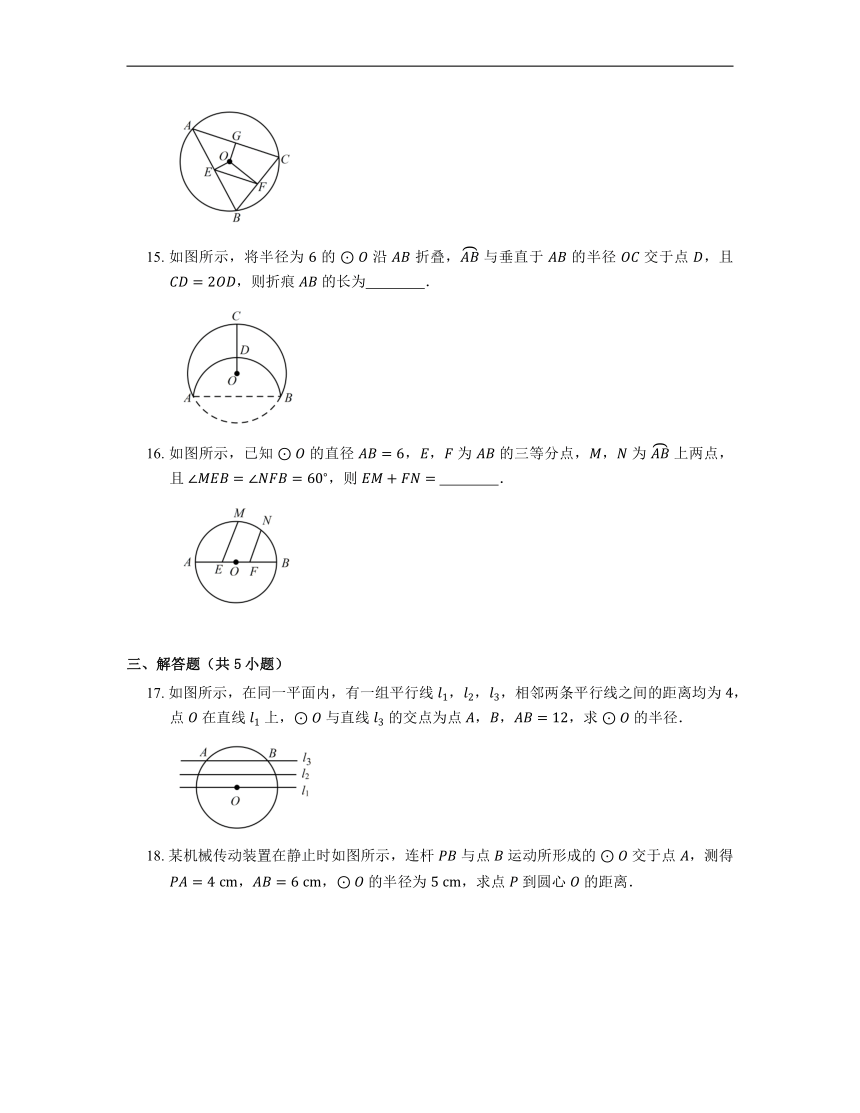
1. 如图所示,在 中,弦 垂直于直径 于点 ,则下列结论:① ;② ;③ ;④ .其中正确的有
A. ①②③④ B. ①②③ C. ②③④ D. ①④
2. 如图所示, 的半径为 ,若 ,则经过点 的弦长可能是
A. B. C. D.
3. 如图所示, 为 的直径,弦 于点 ,已知 ,,则 的直径为
A. B. C. D.
4. 如图所示,在半径为 的 中,, 是互相垂直的两条弦,垂足为点 ,且 ,则 的长为
A. B. C. D.
5. 如图所示,在平面直角坐标系中, 的圆心坐标是 ,半径为 ,函数 的图象被 截得的弦 的长为 ,则 的值是
A. B. C. D.
6. 如图所示,在 内有折线 ,其中 ,,,则 的长为
A. B. C. D.
7. 如图,已知 的半径为 ,弦 长为 ,则点 到 的距离是
A. B. C. D.
8. 如图, 是 的外接圆,,,则弦 的长为
A. B. C. D.
9. 已知 的直径 , 是 的弦,,垂足为 ,且 ,则 的长为
A. B.
C. 或 D. 或
二、填空题(共7小题)
10. 如图所示, 的半径是 , 是 的直径,弦 ,垂足为点 ,若 ,则 的面积是 .
11. 如图所示,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,以点 为圆心, 长为半径作弧,与 轴交于点 ,则点 的坐标为 .
12. 如图所示, 是 的直径, 是弦,点 是 的中点, 交 于点 .连接 ,若 ,,则 的长为 .
13. 如图所示, 是 的直径,矩形 的顶点 , 在 上,顶点 , 在 上,若 的半径为 ,,则 边的长为 .
14. 如图所示, 的半径是 , 是 的内接三角形,过圆心 分别作 ,, 的垂线,垂足分别为点 ,,,连接 .若 ,则 为 .
15. 如图所示,将半径为 的 沿 折叠, 与垂直于 的半径 交于点 ,且 ,则折痕 的长为 .
16. 如图所示,已知 的直径 ,, 为 的三等分点,, 为 上两点,且 ,则 .
三、解答题(共5小题)
17. 如图所示,在同一平面内,有一组平行线 ,,,相邻两条平行线之间的距离均为 ,点 在直线 上, 与直线 的交点为点 ,,,求 的半径.
18. 某机械传动装置在静止时如图所示,连杆 与点 运动所形成的 交于点 ,测得 ,, 的半径为 ,求点 到圆心 的距离.
19. 如图所示,已知 中,, 两弦互相垂直于点 , 被分成 和 两段.
(1)求圆心 到 的距离;
(2)若 半径为 ,求 的长是多少.
20. 如图所示,四边形 和四边形 都为正方形,且点 ,, 在半圆 的直径上,点 ,, 在半圆 的圆弧上,若小正方形边长为 ,求该半圆的半径.
21. 如图所示,在半径为 的扇形 中,,点 是 上的一个动点(不与点 , 重合),,,垂足分别为点 ,.
(1)当 时,求线段 的长.
(2)在 中是否存在长度保持不变的边 如果存在,请指出并求其长度;如果不存在,请说明理由.
答案
1. B
2. C
3. D
4. C
5. B
6. B
7. B
8. C
9. C
【解析】连接 ,.
的直径 ,,,
,,
当 点位置如图所示时,
,,,
,
,
;
当 点位置如图所示时,同理可得 ,
,
,
在 中,.
10.
11.
12.
13.
14.
15.
16.
17. 如图所示,连接 ,过点 作 于点 .
,
.
相邻两条平行线之间的距离均为 ,
.
在 中,
,,
.
的半径为 .
18. 如图所示,连接 ,过点 作 于点 .
则 .
.
在 中,.
在 中,.
19. (1) 如图所示,作 于点 , 于点 .
,
四边形 是矩形.
.
,
.
.
点 到 的距离为 .
(2) 如图所示,连接 ,
在 中,,,
.
,
.
20. 如图所示,连接 ,,.
四边形 为正方形,
.
,,,
.
设 ,则 ,.
在 中,,
在 中,,
,
,解得 ,(舍去).
,即该半圆的半径为 .
21. (1) ,
.
.
(2) 存在, 的长度不变.
理由如下:如图所示,连接 .
过点 作 的垂直平分线,与 交于点 ,与 交于点 ,
则 平分 与 ,
.
在 中,.
,
.
,
.
由垂径定理可知,点 , 分别是 和 的中点,
是 的中位线.
.
一、选择题(共9小题)
1. 如图所示,在 中,弦 垂直于直径 于点 ,则下列结论:① ;② ;③ ;④ .其中正确的有
A. ①②③④ B. ①②③ C. ②③④ D. ①④
2. 如图所示, 的半径为 ,若 ,则经过点 的弦长可能是
A. B. C. D.
3. 如图所示, 为 的直径,弦 于点 ,已知 ,,则 的直径为
A. B. C. D.
4. 如图所示,在半径为 的 中,, 是互相垂直的两条弦,垂足为点 ,且 ,则 的长为
A. B. C. D.
5. 如图所示,在平面直角坐标系中, 的圆心坐标是 ,半径为 ,函数 的图象被 截得的弦 的长为 ,则 的值是
A. B. C. D.
6. 如图所示,在 内有折线 ,其中 ,,,则 的长为
A. B. C. D.
7. 如图,已知 的半径为 ,弦 长为 ,则点 到 的距离是
A. B. C. D.
8. 如图, 是 的外接圆,,,则弦 的长为
A. B. C. D.
9. 已知 的直径 , 是 的弦,,垂足为 ,且 ,则 的长为
A. B.
C. 或 D. 或
二、填空题(共7小题)
10. 如图所示, 的半径是 , 是 的直径,弦 ,垂足为点 ,若 ,则 的面积是 .
11. 如图所示,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,以点 为圆心, 长为半径作弧,与 轴交于点 ,则点 的坐标为 .
12. 如图所示, 是 的直径, 是弦,点 是 的中点, 交 于点 .连接 ,若 ,,则 的长为 .
13. 如图所示, 是 的直径,矩形 的顶点 , 在 上,顶点 , 在 上,若 的半径为 ,,则 边的长为 .
14. 如图所示, 的半径是 , 是 的内接三角形,过圆心 分别作 ,, 的垂线,垂足分别为点 ,,,连接 .若 ,则 为 .
15. 如图所示,将半径为 的 沿 折叠, 与垂直于 的半径 交于点 ,且 ,则折痕 的长为 .
16. 如图所示,已知 的直径 ,, 为 的三等分点,, 为 上两点,且 ,则 .
三、解答题(共5小题)
17. 如图所示,在同一平面内,有一组平行线 ,,,相邻两条平行线之间的距离均为 ,点 在直线 上, 与直线 的交点为点 ,,,求 的半径.
18. 某机械传动装置在静止时如图所示,连杆 与点 运动所形成的 交于点 ,测得 ,, 的半径为 ,求点 到圆心 的距离.
19. 如图所示,已知 中,, 两弦互相垂直于点 , 被分成 和 两段.
(1)求圆心 到 的距离;
(2)若 半径为 ,求 的长是多少.
20. 如图所示,四边形 和四边形 都为正方形,且点 ,, 在半圆 的直径上,点 ,, 在半圆 的圆弧上,若小正方形边长为 ,求该半圆的半径.
21. 如图所示,在半径为 的扇形 中,,点 是 上的一个动点(不与点 , 重合),,,垂足分别为点 ,.
(1)当 时,求线段 的长.
(2)在 中是否存在长度保持不变的边 如果存在,请指出并求其长度;如果不存在,请说明理由.
答案
1. B
2. C
3. D
4. C
5. B
6. B
7. B
8. C
9. C
【解析】连接 ,.
的直径 ,,,
,,
当 点位置如图所示时,
,,,
,
,
;
当 点位置如图所示时,同理可得 ,
,
,
在 中,.
10.
11.
12.
13.
14.
15.
16.
17. 如图所示,连接 ,过点 作 于点 .
,
.
相邻两条平行线之间的距离均为 ,
.
在 中,
,,
.
的半径为 .
18. 如图所示,连接 ,过点 作 于点 .
则 .
.
在 中,.
在 中,.
19. (1) 如图所示,作 于点 , 于点 .
,
四边形 是矩形.
.
,
.
.
点 到 的距离为 .
(2) 如图所示,连接 ,
在 中,,,
.
,
.
20. 如图所示,连接 ,,.
四边形 为正方形,
.
,,,
.
设 ,则 ,.
在 中,,
在 中,,
,
,解得 ,(舍去).
,即该半圆的半径为 .
21. (1) ,
.
.
(2) 存在, 的长度不变.
理由如下:如图所示,连接 .
过点 作 的垂直平分线,与 交于点 ,与 交于点 ,
则 平分 与 ,
.
在 中,.
,
.
,
.
由垂径定理可知,点 , 分别是 和 的中点,
是 的中位线.
.
同课章节目录
