2.7 探索勾股定理（1）课件

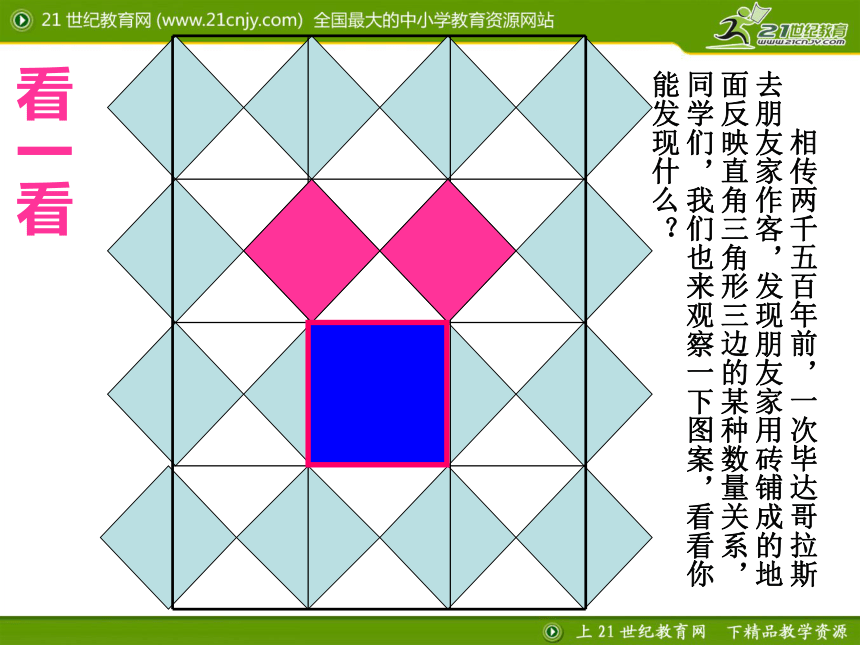
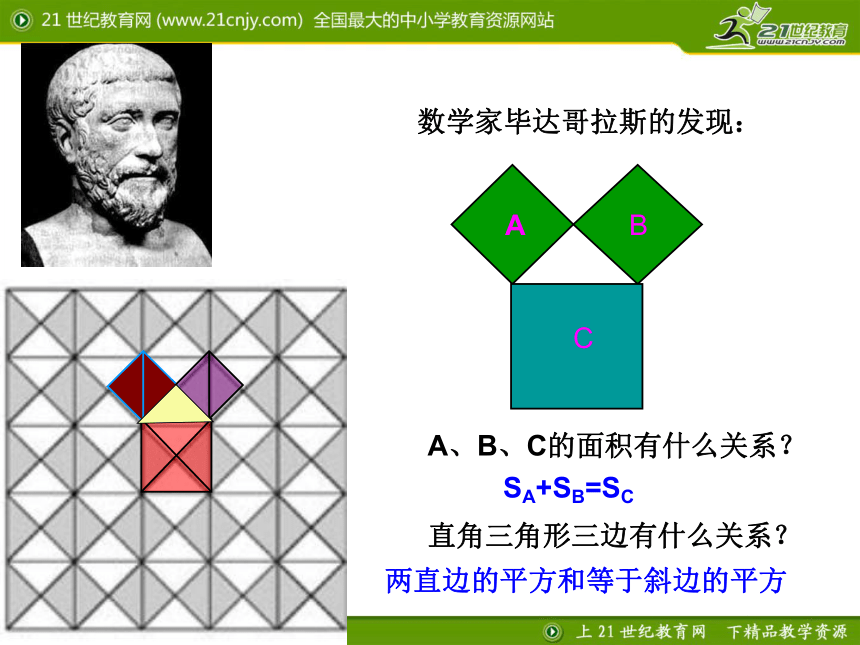
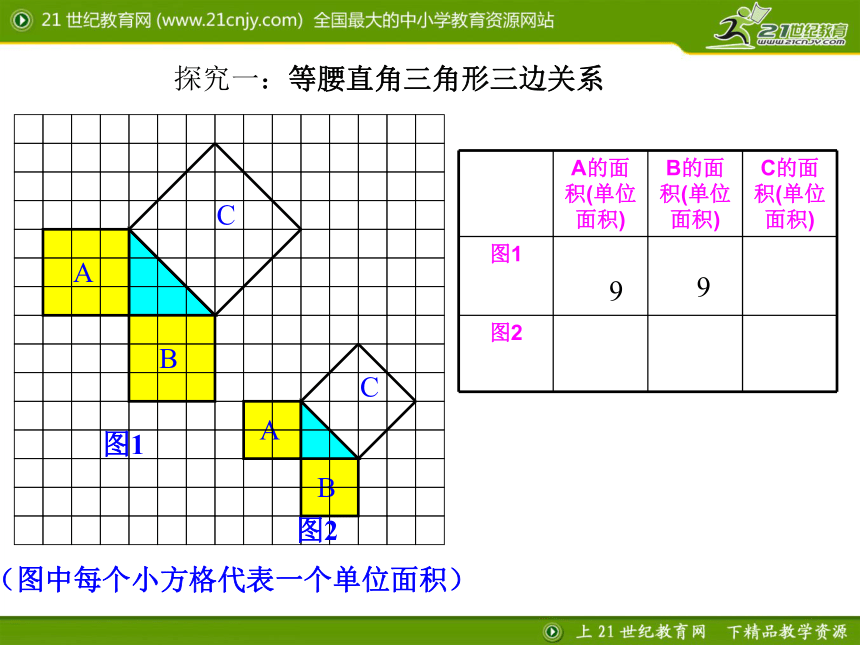
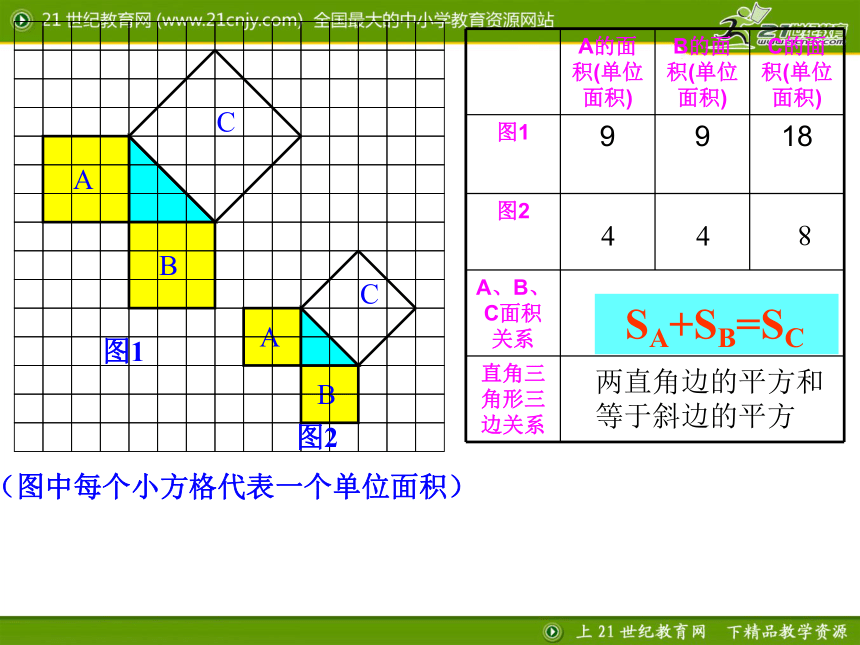
课件17张PPT。2.7探索勾股定理（1）　一、情境引入 会标中央的图案是赵爽弦图，它与“勾股定理”有关，数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号. 2002年世界数学家大会在我国北京召开，下图是本届数学家大会的会标：看一看 相传两千五百年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察一下图案，看看你能发现什么？　　数学家毕达哥拉斯的发现：A、B、C的面积有什么关系？直角三角形三边有什么关系？SA+SB=SC两直边的平方和等于斜边的平方探究一：等腰直角三角形三边关系99 SA+SB=SC448两直角边的平方和
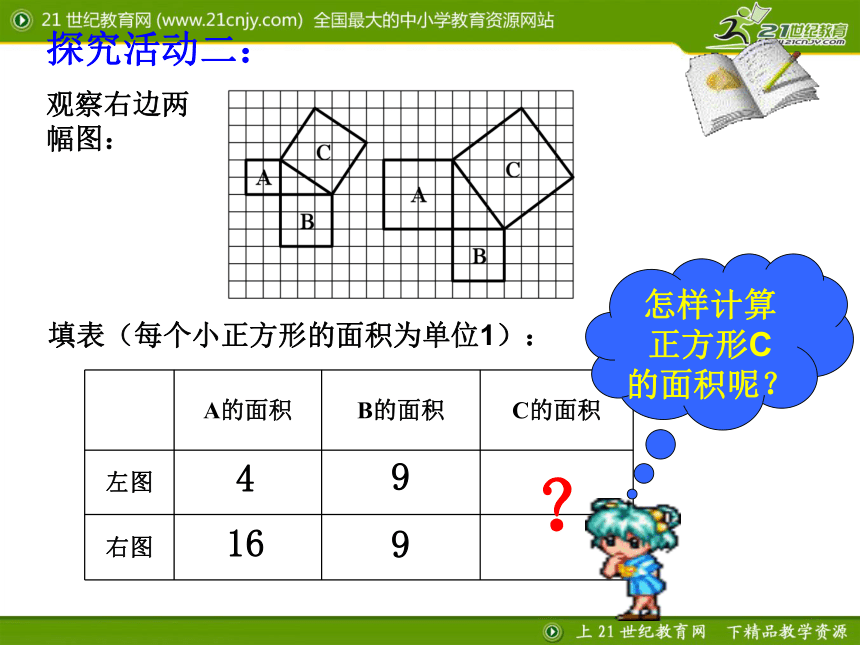
等于斜边的平方探究活动二：观察右边两幅图： 填表（每个小正方形的面积为单位1）：4 ？怎样计算正方形C的面积呢？9 16 9 议一议：　 （1）你能用直角三角形的两直角边的长a，b和斜边长c来表示图中正方形的面积吗？　abcabc勾股定理 直角三角形两条直角边的平方
和等于斜边的平方.∴ a2+b2=c2在Rt△ABC中∵ ∠C=Rt∠(AC2+BC2=AB2)勾股弦 两千多年前，古希腊有个哥拉 斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾 股 世 界国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前 两千多年前，古希腊有个毕达哥拉斯学派，他们发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票. 我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中.(1)若a=3, b=2, 求c;例1：已知ΔABC中，∠C=Rt∠，BC=a，
AC=b，AB=c。(2)若a=15,c=17,求b;(3)若c=34，a:b=8:15，求a、b;试一试1、在△ABC中，∠C= .（1）若a=5，b=12，则c= .
（2）若c=4，b= ，则a= . 2、已知△ABC的三边分别是a，b，c，
若∠B=Rt∠，则有关系式（ ）A.a2+b2=c2B.a2+c2=b2C.a2-b2=c2D.b2+c2=a23、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=1444．如图，所有的四边形都是正方形，所有的三角形
都是直角三角形，其中最大的正方形的边长为7cm,则
正方形A，B，C，D的面积之和为___________cm2。495.在数轴上画出表示 的点。0C例2、 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米) 印度数学家什迦逻（1141年-1225年？）
曾提出过“荷花问题”：
“平平湖水清可鉴，面上半尺生红莲；
出泥不染亭亭立，忽被强风吹一边，
渔人观看忙向前，花离原位二尺远；
能算诸君请解题，湖水如何知深浅？”20.5CAB你会算吗？D