浙教版数学九年级上册4.3相似三角形 课件(共13张PPT)
文档属性
| 名称 | 浙教版数学九年级上册4.3相似三角形 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 488.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 20:11:41 | ||
图片预览

文档简介
(共13张PPT)
4.3 相似三角形
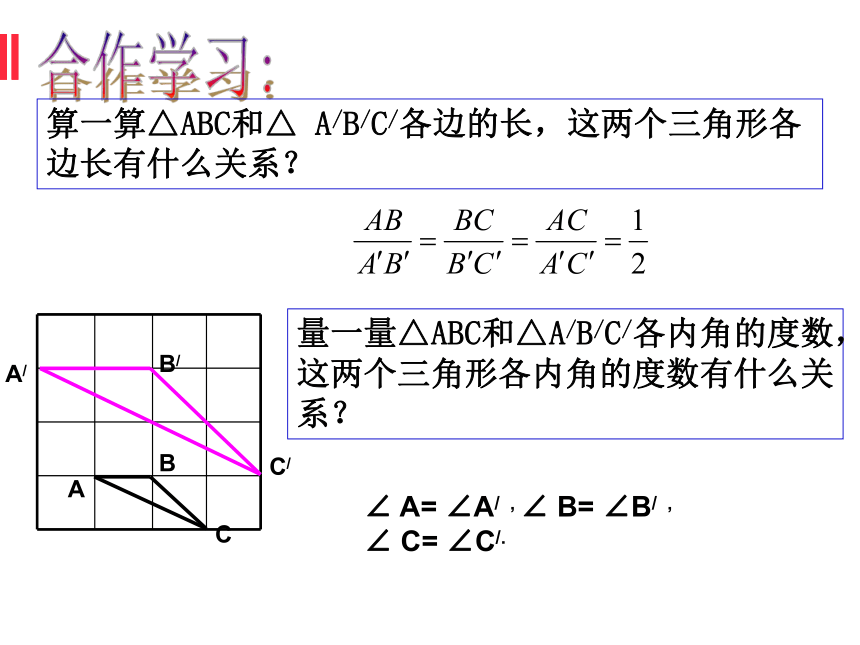
算一算△ABC和△ A/B/C/各边的长,这两个三角形各边长有什么关系?
A
B
C
A/
B/
C/
∠ A= ∠A/ , ∠ B= ∠B/ ,
∠ C= ∠C/.
量一量△ABC和△A/B/C/各内角的度数,这两个三角形各内角的度数有什么关系?
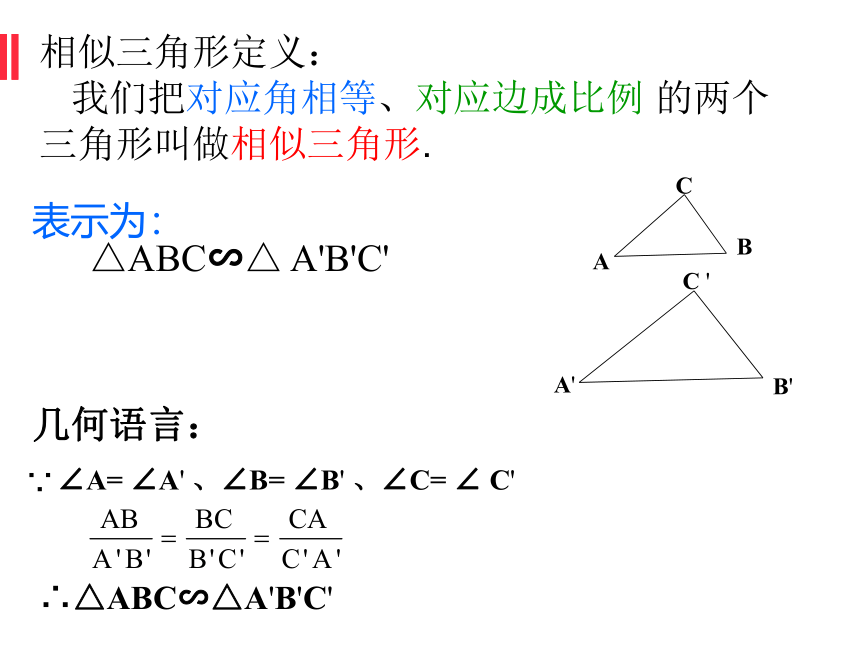
相似三角形定义:
我们把对应角相等、对应边成比例 的两个三角形叫做相似三角形.
C
A
B
A'
B'
C '
∵
∠A= ∠A' 、∠B= ∠B' 、∠C= ∠ C'
△ABC∽△A'B'C'
∴
几何语言:
表示为:
△ABC∽△ A'B'C'
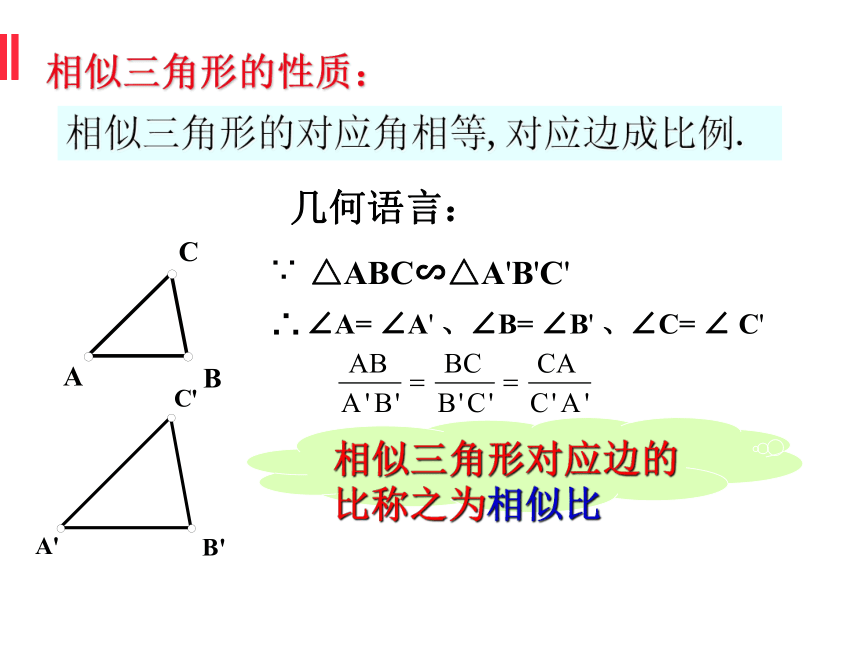
相似三角形的对应角相等,对应边成比例.
相似三角形对应边的比称之为相似比
∵
△ABC∽△A'B'C'
∠A= ∠A' 、∠B= ∠B' 、∠C= ∠ C'
∴
相似三角形的性质:
几何语言:
A
B
C
D
E
F
2cm
3cm
求:△ABC与△DEF对应边的比
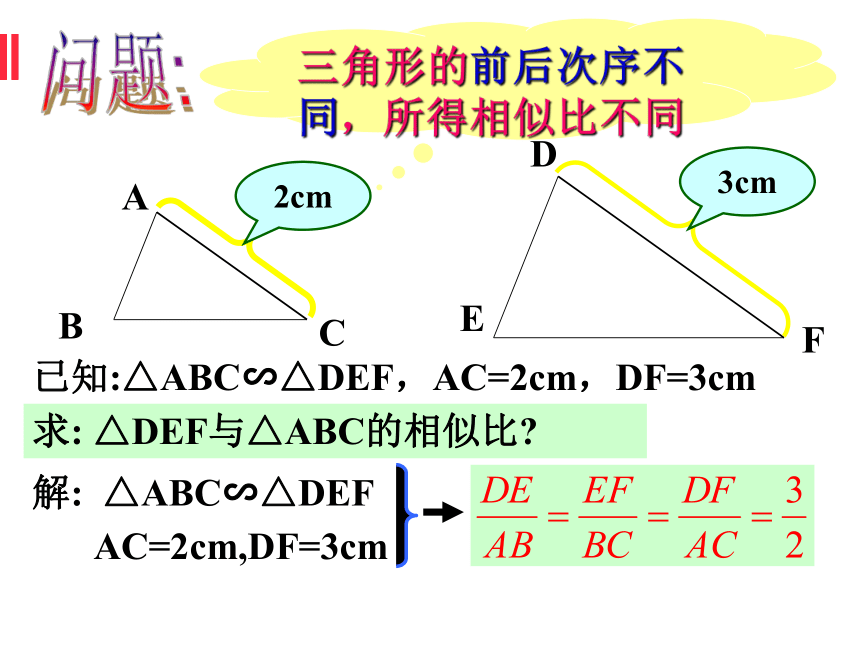
已知:△ABC∽△DEF,AC=2cm,DF=3cm
解: △ABC∽△DEF
AC=2cm,DF=3cm
求: △DEF与△ABC的相似比
三角形的前后次序不同,所得相似比不同
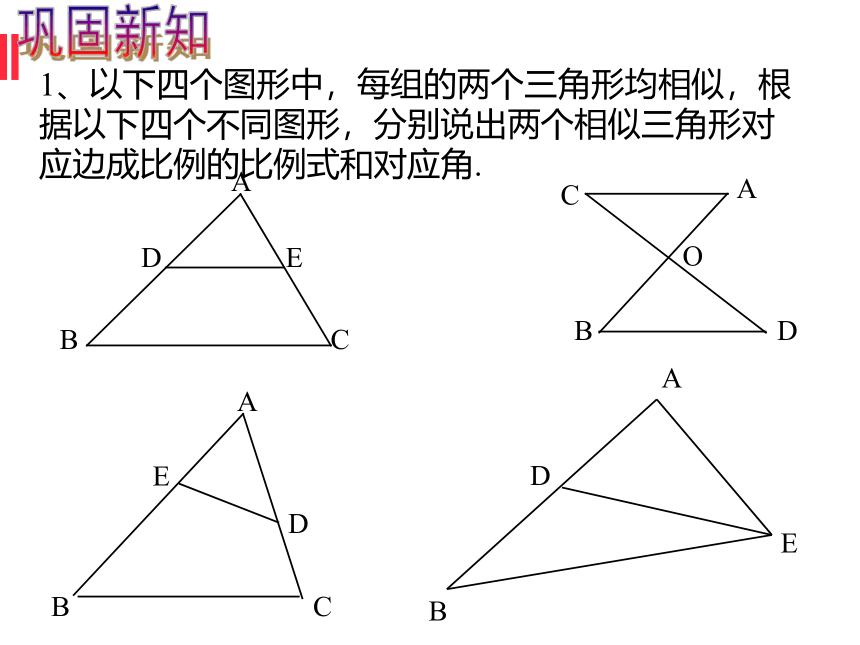
1、以下四个图形中,每组的两个三角形均相似,根据以下四个不同图形,分别说出两个相似三角形对应边成比例的比例式和对应角.
A
B
C
D
E
A
D
O
C
B
A
D
E
C
B
A
B
E
D
已知:如图, D、E分别是AB、AC的中点.
求证:△ADE∽ △ABC.
1
2
如图,D、E分别是△ABC的AB、AC边上的点,△ABC∽ △ADE.已知AD:DB=1:2,BC=9cm.求DE的长.
A
B
C
D
E
129页课内练习第3题
如果两个三角形都与第三个三角形相似,那么这两个三角形相似吗?
1.在下面两组图形中,每组的两个三角形相似,α表示已知数,试分别确定α,x的值
(1)
130页课后作业第4题
(2)
2.如图,△ABC∽ △ACD,点D在AB上,已知AC=3cm,AD=2cm,求AB的长
130页课后作业第5题
如图:矩形ABCD, △ABE∽△DEF,若AB=6,AE=6,DE=3,求EF的长度
4.3 相似三角形
算一算△ABC和△ A/B/C/各边的长,这两个三角形各边长有什么关系?
A
B
C
A/
B/
C/
∠ A= ∠A/ , ∠ B= ∠B/ ,
∠ C= ∠C/.
量一量△ABC和△A/B/C/各内角的度数,这两个三角形各内角的度数有什么关系?
相似三角形定义:
我们把对应角相等、对应边成比例 的两个三角形叫做相似三角形.
C
A
B
A'
B'
C '
∵
∠A= ∠A' 、∠B= ∠B' 、∠C= ∠ C'
△ABC∽△A'B'C'
∴
几何语言:
表示为:
△ABC∽△ A'B'C'
相似三角形的对应角相等,对应边成比例.
相似三角形对应边的比称之为相似比
∵
△ABC∽△A'B'C'
∠A= ∠A' 、∠B= ∠B' 、∠C= ∠ C'
∴
相似三角形的性质:
几何语言:
A
B
C
D
E
F
2cm
3cm
求:△ABC与△DEF对应边的比
已知:△ABC∽△DEF,AC=2cm,DF=3cm
解: △ABC∽△DEF
AC=2cm,DF=3cm
求: △DEF与△ABC的相似比
三角形的前后次序不同,所得相似比不同
1、以下四个图形中,每组的两个三角形均相似,根据以下四个不同图形,分别说出两个相似三角形对应边成比例的比例式和对应角.
A
B
C
D
E
A
D
O
C
B
A
D
E
C
B
A
B
E
D
已知:如图, D、E分别是AB、AC的中点.
求证:△ADE∽ △ABC.
1
2
如图,D、E分别是△ABC的AB、AC边上的点,△ABC∽ △ADE.已知AD:DB=1:2,BC=9cm.求DE的长.
A
B
C
D
E
129页课内练习第3题
如果两个三角形都与第三个三角形相似,那么这两个三角形相似吗?
1.在下面两组图形中,每组的两个三角形相似,α表示已知数,试分别确定α,x的值
(1)
130页课后作业第4题
(2)
2.如图,△ABC∽ △ACD,点D在AB上,已知AC=3cm,AD=2cm,求AB的长
130页课后作业第5题
如图:矩形ABCD, △ABE∽△DEF,若AB=6,AE=6,DE=3,求EF的长度
同课章节目录
