1.3绝对值 课件(共20张PPT)
图片预览







文档简介
(共20张PPT)
1.3绝对值
浙教版版七年级上册
教学目标
2.会求一个数的绝对值;会求绝对值已知的数.
1.理解绝对值的概念及其几何意义.
3.理解互为相反数的两个数的绝对值相等.
4.了解绝对值的简单应用.
复习回顾
1.什么是数轴?
规定了原点、正方向、单位长度的直线.
三要素
2.什么相反数?
只有符号不同的两个数互为相反数.
特别地,0的相反数是0.互为相反数的2个数之和为0.
3.在数轴上,表示互为相反数(0除外)的两个点有什么特征?
位于原点的两侧,并且到原点的距离相等.
数轴上的点表示的数沿着数轴的正方向越来越大
情境导入
城市里出租车一般按实际载客行驶的里程收费,与行驶的路线、方向无关.
合作学习
1. 甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记做______km,乙车向西行驶10km到达B处,记做______km.
以O为原点,取适当地单位长度画数轴,并在数轴上标出A,B的位置,则A,B两点与原点的距离分别是多少?它们的实际意义是什么?
0
2
4
6
8
10
-2
-4
-6
-8
-10
A
B
10
10
+6
-6
A、B两点与原点距离分别是6 km,它们的实际意义是甲、乙两辆出租车距出发地6 km.
2. 数轴上表示-4和4的点到原点的距离分别是多少?表示和的点呢?
数轴上表示-4和4的点到原点的距离分别是4,
表示 和 的点到原点的距离分别是 .
新知讲解
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
绝对值的意义及求法
你能举出生活中应用到绝对值解决问题的例子吗?
同步训练
0
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
3
3
数轴上表示+3的点到原点的距离是_____.
数轴上表示-3的点到原点的距离是_____.
数轴上表示-1.5 的点到原点的距离是_____.
数轴上表示 0 的点到原点的距离_____.
3
3
0
+3的绝对值是3
记做|+3|= 3
3的绝对值是3
记做|3|= 3
-1.5 的绝对值是1.5
0的绝对值是0
记做|0|= 0
1.5
记做 | -1.5 | = 1.5
典例精析
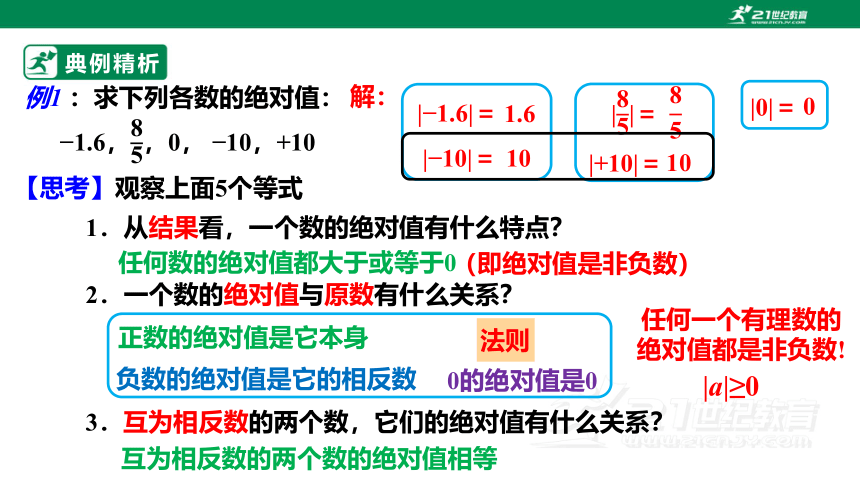
例1 :求下列各数的绝对值:
1.6,,0, 10,+10
| 1.6|=
1.6
解:
||=
|0|=
0
| 10|=
10
|+10|=
10
【思考】观察上面5个等式
1.从结果看,一个数的绝对值有什么特点?
任何数的绝对值都大于或等于0
(即绝对值是非负数)
2.一个数的绝对值与原数有什么关系?
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
3.互为相反数的两个数,它们的绝对值有什么关系?
互为相反数的两个数的绝对值相等
法则
任何一个有理数的绝对值都是非负数!
|a|≥0
归纳总结
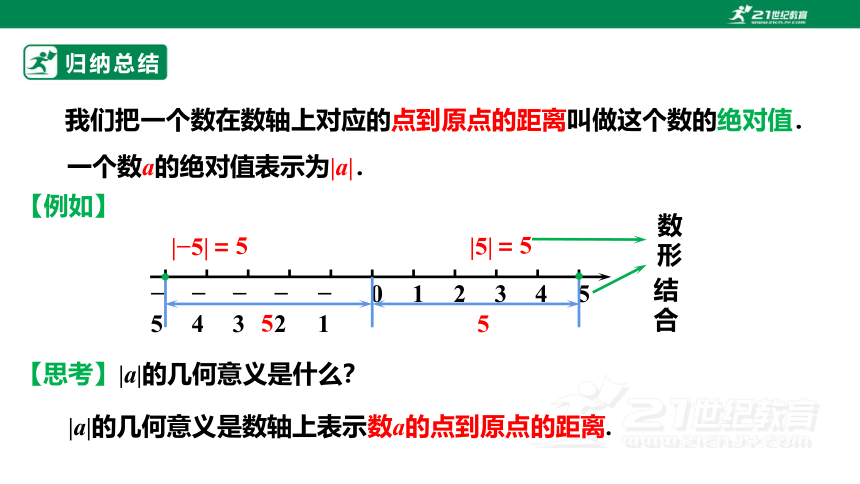
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
一个数a的绝对值表示为|a|.
0
1
2
3
4
1
2
3
4
5
5
5
5
【例如】
| 5|=
5
|5|=
5
【思考】|a|的几何意义是什么?
数
形
结合
|a|的几何意义是数轴上表示数a的点到原点的距离.
做一做
1.正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3) 当a = 0时,|a|=__.
a
-a
0
3.0的绝对值是0
2.负数的绝对值是它的相反数
字母a表示一个有理数,你知道a的绝对值等于什么吗
思考:
(口答)说出下列各数的绝对值:
7,2.05,0,1000,
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
典例精析
例2:求绝对值等于4的数.
解:因为数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和表示 4的点M,所以绝对值等于4的数是+4和 4.
几何意义?
0
1
2
3
4
1
2
3
4
5
5
4个单位长度
4个单位长度
P
M
方法(一)
方法(二)
∵|+4|=4,| 4|=4,
绝对值等于4的数是+4和 4.
1、判断:
(1)绝对值最小的数是0。( )
(2)一个数的绝对值一定是正数。( )
(3)一个数的绝对值不可能是负数。( )
(4)互为相反数的两个数,它们的绝对值一定相等。( )
(5)一个数的绝对值越大,表示它的点在数轴上离原点越近。( )
课堂练习
2、计算:
(1)1+| 6|=( ). (2)|6| | 2|=( ).
(3)| 1| + | 3|=( ). (4)|+8| | 8|= ( ).
7
4
4
0
3、绝对值最小的数是________;绝对值最小的负整数是________;一个数的绝对值是它本身,那么这个数是__________.
0
1
正数或0
(非负数)
4、绝对值等于3的数是_________.
3或 3
5、绝对值小于3的整数有_____个,分别是_____________________.
6、绝对值不大于6的整数中,最大的数是_____,最小的数是_____.
5
2、 1、0、1、2
6
6
7、如图,图中数轴的单位长度为1.如果点B,C所表示的数的绝对值相等,那么点A表示的数是________.
5
8、一辆出租车从A站出发,先向东行驶12km,接着向西行驶8km,然后又向东行驶4km.
(1)画一条数轴,以原点表示A站,向东为正方向,在数轴上表示出租车每次行驶的终点位置.
(2)求各次路程的绝对值和.这个数据的实际意义是什么
解:(1)如下图:
(2)第一次终点位置+12,第二次终点位置+4,第三次终点位置+8.(2) |+12|+ |-8| + |+4|=24 ( km)它的实际意义是出租车行驶的总里程是24km.
1.绝对值的定义:
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值法则:
(1) 正数的绝对值是它本身;
(2) 负数的绝对值是它的相反数;
(3) 0的绝对值是0;
(4) 互为相反数的两个数的绝对值相等.
3.数学思想:数形结合
课堂总结
通过本节课的交流,你有什么体验或收获
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
|a| = | a|
|a|≥0
作业布置
1.作业本
2.教材练习题
拓展提升
1、已知|a-5|+|b+2|=0,则a=______,b=______.
2、如图,若a的绝对值是b的绝对值的3倍,则数轴的原点可以是点________.
3、阅读材料:
数轴上表示a的点可简称为“点a”,|a|就是点a到原点的距离,如|-3|指数轴上的点-3到原点的距离,而|a|可以写成|a-0|,因此这种理解可以延伸,即|a-b|指数轴上点a到点b的距离.
如:|3-2|指数轴上点3到点2的距离,值为1;
|-3-(-2)|指数轴上点-3到点-2的距离,值为1.
请根据材料回答下列问题:
(1)|a-1|指数轴上点a到点_____的距离;若|a-1|的值为1,则a=_______.
(2)若|a-3|与|a-(-2)|的和为7,求a的值.
趣味数学
如图,已知半径为1个单位长度的圆上有一点A与数轴上的原点重合,AB是圆的直径.
(1)把圆片沿数轴向右滚动1周,点A到达数轴上点C的位置,点C表示的数是_____.
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是______.
(3)把圆片在数轴上向右滚动的周数记为正数,向左滚动的周数记为负数,运动情况记录如下:+2,-1,+3,-4,-3.
①第几次滚动后,点A距离原点最近?第几次滚动后,点A距离原点最远?
②当圆片结束运动时,点A运动的路程是多少?
板书设计
1.3绝对值
1. 定义:
2. 法则:
3.数学思想:数形结合
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
|a|≥0
|a| = | a|
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3绝对值
浙教版版七年级上册
教学目标
2.会求一个数的绝对值;会求绝对值已知的数.
1.理解绝对值的概念及其几何意义.
3.理解互为相反数的两个数的绝对值相等.
4.了解绝对值的简单应用.
复习回顾
1.什么是数轴?
规定了原点、正方向、单位长度的直线.
三要素
2.什么相反数?
只有符号不同的两个数互为相反数.
特别地,0的相反数是0.互为相反数的2个数之和为0.
3.在数轴上,表示互为相反数(0除外)的两个点有什么特征?
位于原点的两侧,并且到原点的距离相等.
数轴上的点表示的数沿着数轴的正方向越来越大
情境导入
城市里出租车一般按实际载客行驶的里程收费,与行驶的路线、方向无关.
合作学习
1. 甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记做______km,乙车向西行驶10km到达B处,记做______km.
以O为原点,取适当地单位长度画数轴,并在数轴上标出A,B的位置,则A,B两点与原点的距离分别是多少?它们的实际意义是什么?
0
2
4
6
8
10
-2
-4
-6
-8
-10
A
B
10
10
+6
-6
A、B两点与原点距离分别是6 km,它们的实际意义是甲、乙两辆出租车距出发地6 km.
2. 数轴上表示-4和4的点到原点的距离分别是多少?表示和的点呢?
数轴上表示-4和4的点到原点的距离分别是4,
表示 和 的点到原点的距离分别是 .
新知讲解
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
绝对值的意义及求法
你能举出生活中应用到绝对值解决问题的例子吗?
同步训练
0
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
3
3
数轴上表示+3的点到原点的距离是_____.
数轴上表示-3的点到原点的距离是_____.
数轴上表示-1.5 的点到原点的距离是_____.
数轴上表示 0 的点到原点的距离_____.
3
3
0
+3的绝对值是3
记做|+3|= 3
3的绝对值是3
记做|3|= 3
-1.5 的绝对值是1.5
0的绝对值是0
记做|0|= 0
1.5
记做 | -1.5 | = 1.5
典例精析
例1 :求下列各数的绝对值:
1.6,,0, 10,+10
| 1.6|=
1.6
解:
||=
|0|=
0
| 10|=
10
|+10|=
10
【思考】观察上面5个等式
1.从结果看,一个数的绝对值有什么特点?
任何数的绝对值都大于或等于0
(即绝对值是非负数)
2.一个数的绝对值与原数有什么关系?
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
3.互为相反数的两个数,它们的绝对值有什么关系?
互为相反数的两个数的绝对值相等
法则
任何一个有理数的绝对值都是非负数!
|a|≥0
归纳总结
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
一个数a的绝对值表示为|a|.
0
1
2
3
4
1
2
3
4
5
5
5
5
【例如】
| 5|=
5
|5|=
5
【思考】|a|的几何意义是什么?
数
形
结合
|a|的几何意义是数轴上表示数a的点到原点的距离.
做一做
1.正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3) 当a = 0时,|a|=__.
a
-a
0
3.0的绝对值是0
2.负数的绝对值是它的相反数
字母a表示一个有理数,你知道a的绝对值等于什么吗
思考:
(口答)说出下列各数的绝对值:
7,2.05,0,1000,
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
典例精析
例2:求绝对值等于4的数.
解:因为数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和表示 4的点M,所以绝对值等于4的数是+4和 4.
几何意义?
0
1
2
3
4
1
2
3
4
5
5
4个单位长度
4个单位长度
P
M
方法(一)
方法(二)
∵|+4|=4,| 4|=4,
绝对值等于4的数是+4和 4.
1、判断:
(1)绝对值最小的数是0。( )
(2)一个数的绝对值一定是正数。( )
(3)一个数的绝对值不可能是负数。( )
(4)互为相反数的两个数,它们的绝对值一定相等。( )
(5)一个数的绝对值越大,表示它的点在数轴上离原点越近。( )
课堂练习
2、计算:
(1)1+| 6|=( ). (2)|6| | 2|=( ).
(3)| 1| + | 3|=( ). (4)|+8| | 8|= ( ).
7
4
4
0
3、绝对值最小的数是________;绝对值最小的负整数是________;一个数的绝对值是它本身,那么这个数是__________.
0
1
正数或0
(非负数)
4、绝对值等于3的数是_________.
3或 3
5、绝对值小于3的整数有_____个,分别是_____________________.
6、绝对值不大于6的整数中,最大的数是_____,最小的数是_____.
5
2、 1、0、1、2
6
6
7、如图,图中数轴的单位长度为1.如果点B,C所表示的数的绝对值相等,那么点A表示的数是________.
5
8、一辆出租车从A站出发,先向东行驶12km,接着向西行驶8km,然后又向东行驶4km.
(1)画一条数轴,以原点表示A站,向东为正方向,在数轴上表示出租车每次行驶的终点位置.
(2)求各次路程的绝对值和.这个数据的实际意义是什么
解:(1)如下图:
(2)第一次终点位置+12,第二次终点位置+4,第三次终点位置+8.(2) |+12|+ |-8| + |+4|=24 ( km)它的实际意义是出租车行驶的总里程是24km.
1.绝对值的定义:
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值法则:
(1) 正数的绝对值是它本身;
(2) 负数的绝对值是它的相反数;
(3) 0的绝对值是0;
(4) 互为相反数的两个数的绝对值相等.
3.数学思想:数形结合
课堂总结
通过本节课的交流,你有什么体验或收获
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
|a| = | a|
|a|≥0
作业布置
1.作业本
2.教材练习题
拓展提升
1、已知|a-5|+|b+2|=0,则a=______,b=______.
2、如图,若a的绝对值是b的绝对值的3倍,则数轴的原点可以是点________.
3、阅读材料:
数轴上表示a的点可简称为“点a”,|a|就是点a到原点的距离,如|-3|指数轴上的点-3到原点的距离,而|a|可以写成|a-0|,因此这种理解可以延伸,即|a-b|指数轴上点a到点b的距离.
如:|3-2|指数轴上点3到点2的距离,值为1;
|-3-(-2)|指数轴上点-3到点-2的距离,值为1.
请根据材料回答下列问题:
(1)|a-1|指数轴上点a到点_____的距离;若|a-1|的值为1,则a=_______.
(2)若|a-3|与|a-(-2)|的和为7,求a的值.
趣味数学
如图,已知半径为1个单位长度的圆上有一点A与数轴上的原点重合,AB是圆的直径.
(1)把圆片沿数轴向右滚动1周,点A到达数轴上点C的位置,点C表示的数是_____.
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是______.
(3)把圆片在数轴上向右滚动的周数记为正数,向左滚动的周数记为负数,运动情况记录如下:+2,-1,+3,-4,-3.
①第几次滚动后,点A距离原点最近?第几次滚动后,点A距离原点最远?
②当圆片结束运动时,点A运动的路程是多少?
板书设计
1.3绝对值
1. 定义:
2. 法则:
3.数学思想:数形结合
|a|=
a
0
a
(a>0)
(a=0)
(a<0)
|a|≥0
|a| = | a|
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
