2.1.2 有理数的加法 课件(共23张PPT)
文档属性
| 名称 | 2.1.2 有理数的加法 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 15:13:42 | ||
图片预览







文档简介
(共23张PPT)
2.1有理数的加法(2)
浙教版版七年级上册
教学目标
2.理解加法的运算律.
1.通过“合作学习”活动,体验探索数学规律的思想和方法.
3.掌握多个有理数相加的顺序和方法,探索利用运算律简化运算过程.
4.灵活运用有理数的加法解决简单实际问题.
复习回顾
有理数加法法则
1.同号两数相加,取与加数相同的符号,并把绝对值相加.
2.异号两数相加,取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
4.一个数同0相加,仍得这个数.
3.互为相反数的两个数相加得0.
有理数加法运算的一般步骤
2.确定运算结果的符号.
3.进行绝对值运算.
1.判断加数的符号类型(同号or异号).
问题导入
比一比,
看谁算得快!
(2)
你运用了什么方法使计算简便?
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
思考:
在有理数运算中,这些运算律是否还成立呢?
(1)99+17+1+83
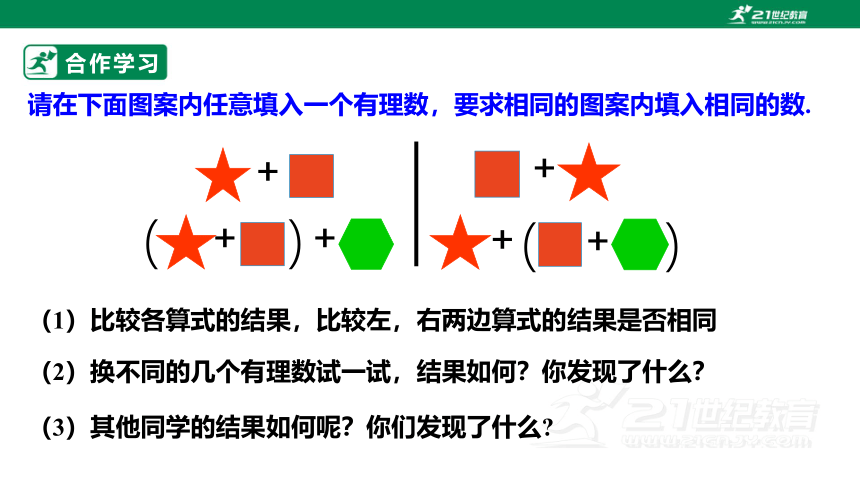
合作学习
请在下面图案内任意填入一个有理数,要求相同的图案内填入相同的数.
(1)比较各算式的结果,比较左,右两边算式的结果是否相同
(3)其他同学的结果如何呢?你们发现了什么
(2)换不同的几个有理数试一试,结果如何?你发现了什么?
+
+
+
+
( )
+
+
( )
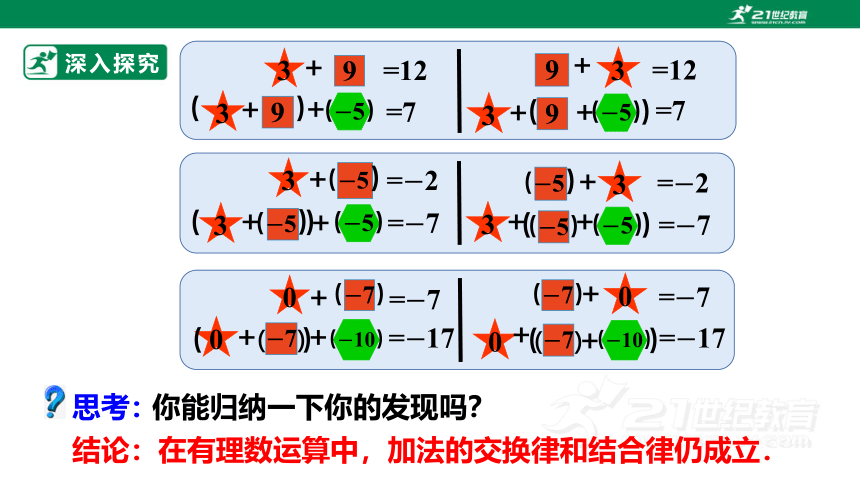
深入探究
结论:在有理数运算中,加法的交换律和结合律仍成立.
3
9
+
3
9
+
(5)
3
9
+
+
( )
3
9
+
(5)
+
( )
=12
=7
=12
=7
3
(5)
+
3
(5)
+
3
(5)
+
(5)
+
( )
=2
=7
=2
0
(7)
+
0
(7)
+
0
(7)
+
(10)
+
( )
=7
=17
=7
(5)
3
(5)
+
+
( )
=7
(10)
0
(7)
+
+
( )
=17
你能归纳一下你的发现吗?
思考:
归纳总结
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
文字语言
符号语言
文字语言
符号语言
典例精析
例3: 计算:
(1)15+13)+18; (2)(2.48)+4.33+(7.52)+(4.33);
(3) .
(1)原式15+18+(13)
33+(13) 20
(15+18)+(13)
加法交换律
加法结合律
符号相同的先结合
(2)原式(2.48)+(7.52)+(+4.33)+(4.33)
[(2.48)+(7.52)]+[(+4.33)+(4.33)]
(10)+0 10
能凑整的先凑整
互为相反数的先结合
解:
(3)原式=+
+(1)
分母相同的先结合
=
归纳总结
使用运算律通常有下列几种方法:
(1)能凑整的先凑整简称凑整结合法;
(2)把正数与负数分别结合在一起再相加简称同号结合法;
(3)有相反数的先把相反数相加简称相反数结合法;
(4)遇到分数,先把同分母的数相加,简称同分母结合法.
1、计算:
(1)5+(-7)+8
(2)(- )+ +(- )
(3)(-3.5)+[3+(-1.5)]
答案: 6
答案: -
答案: -2
课内练习
课内练习
2、用简便方法计算下列各题:
(1)14+(4)+(1)+16 +(5) (2)(18.65)+(7.25)+(+18.15)+(+7.25)
(3)(2.25)+(+(+(+0.125)
解:
(1)原式 (14+16)+[(4)+(1)+(5)] 30+(10) 20
(2)原式[(18.65)+(+18.15)]+[(7.25)+(+7.25)](0.5)+0 = 0.5
(3)原式 [(2.25)+() ]+[()+()] (3)+()
典例精析
例4: 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
你可以画一个示意图表示行驶过程吗?
思考1:
典例精析
思考2:
你可以列算式解决这个问题吗?
例4: 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
和方向有关
和方向无关
解:向东记为正,根据题意得:
(+15)+(25)+(+20)+(35)
=(15+20)+[(25)+(35)]
=25(m);
|+15|+|25|+|+20|+|35|
=15+25+20+35
=95(m).
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
同步训练
检修小组乘汽车沿公路检修线路(约定前进为正,后退为负),某天自A地出发到收工时所走的路程(单位:千米)为:11,-5,3,-4,8,14,-6,12,-9,6.
(1)收工时离A地有多少千米?
(2)若每千米耗油0.2升,则自A地出发到收工时共耗油多少升?
(1)11+(-5)+3+(-4)+8+14+(-6)+12+(-9)+6=30(千米).
答:收工时离A地有30千米.
(2)|+11|+|-5|+|+3|+|-4|+|+8|+|+14|+|-6|+|+12|+|-9|+|+6|
=78(千米).
78×0.2=15.6(升).
答:自A地出发到收工时共耗油15.6升.
解:
(2)任何两数相加,和不小于任何一个加数。
1. 数扩展到有理数之后,下面这些结论还成立吗?
请说明理由(如果认为结论不成立,请举例说明):
(1)若两个数的和是0,则这两个数都是0;
探究活动
不成立.例如:(3)+3=0,但30,30.
不唯一,互为相反数即可.
不成立.例如:10+()=3,但为3,小于加数10.
不唯一,异号相加即可.
课堂练习
1、7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应用了 ( )
A.加法交换律 B.加法结合律 C.分配律 D.加法交换律与结合律
D
2、下列交换加数的位置的变形中,错误的是 ( )
A.30+(-20)=(-20)+30 B.(-5)+(-13)=(-13)+(-5)
C.(-37)+16=16+(-37) D.10+(-20)=20+(-10)
3、计算6+(-3.5)+(+2.5)时,较好的方法是 ( )
A.按顺序进行计算 B.同号的数先相加
C.后面的两个数先相加 D.以上的方法都不对
D
C
4、若三个不相等的有理数的和为0,则下列结论正确的是 ( )
A. 三个数全是0 B. 至少有两个数是负数
C. 至少有一个数是负数 D. 至少有两个数是正数
C
5、用简便方法计算,并说明有关理由.
(1)12+(-18)+4;
(2)8+(-6)+5+(-8);
(3)(-2.4)+4.56+(-5.6)+(-4.56).
(2)原式=8+(-8)+(-6)+5=(-6)+5=-1.
解: (1)原式=12+4+(-18)=16+(-18)=-2.
(3)原式=[(-2.4)+(-5.6)]+[4.56+(-4.56)]=(-8)+0=-8.
6、有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,
则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6 +3 =300+3=303
答:这6筐蔬菜的总质量是303kg.
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
课堂总结
通过本节课的交流,你有什么体验或收获
一、加法的运算律
1、加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列几种方法:
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
作业布置
1.作业本
2.教材练习题
拓展提升
2、如图,在一个由6个圆圈组成的三角形里,将-15到-20这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和S都相等,那么S的最小值是 ( )
A. -53 B. -54 C. -56 D. -57
1、9个全不相等的有理数之和为0,这9个有理数中 ( )
A. 至少有一个为0 B. 至少有4个正数
C. 至少有一个负数 D. 至多有5个负数
C
B
趣味数学
“洛书”是世界上最古老的一个三阶幻方,它有三行三列,三横行的三个数之和、三竖列的三个数之和、两对角线的三个数之和都等于15.其实幻方就是把一些有规律且不相等的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等.如图,若将1~9填入幻方内,则a-b的值是________.
板书设计
2.1有理数的加法(2)
一、加法运算律
1、加法交换律:a+b=b+a
2、加法结合律: (a+b)+c=a+(b+c)
二、简便方法
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.1有理数的加法(2)
浙教版版七年级上册
教学目标
2.理解加法的运算律.
1.通过“合作学习”活动,体验探索数学规律的思想和方法.
3.掌握多个有理数相加的顺序和方法,探索利用运算律简化运算过程.
4.灵活运用有理数的加法解决简单实际问题.
复习回顾
有理数加法法则
1.同号两数相加,取与加数相同的符号,并把绝对值相加.
2.异号两数相加,取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
4.一个数同0相加,仍得这个数.
3.互为相反数的两个数相加得0.
有理数加法运算的一般步骤
2.确定运算结果的符号.
3.进行绝对值运算.
1.判断加数的符号类型(同号or异号).
问题导入
比一比,
看谁算得快!
(2)
你运用了什么方法使计算简便?
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
思考:
在有理数运算中,这些运算律是否还成立呢?
(1)99+17+1+83
合作学习
请在下面图案内任意填入一个有理数,要求相同的图案内填入相同的数.
(1)比较各算式的结果,比较左,右两边算式的结果是否相同
(3)其他同学的结果如何呢?你们发现了什么
(2)换不同的几个有理数试一试,结果如何?你发现了什么?
+
+
+
+
( )
+
+
( )
深入探究
结论:在有理数运算中,加法的交换律和结合律仍成立.
3
9
+
3
9
+
(5)
3
9
+
+
( )
3
9
+
(5)
+
( )
=12
=7
=12
=7
3
(5)
+
3
(5)
+
3
(5)
+
(5)
+
( )
=2
=7
=2
0
(7)
+
0
(7)
+
0
(7)
+
(10)
+
( )
=7
=17
=7
(5)
3
(5)
+
+
( )
=7
(10)
0
(7)
+
+
( )
=17
你能归纳一下你的发现吗?
思考:
归纳总结
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
文字语言
符号语言
文字语言
符号语言
典例精析
例3: 计算:
(1)15+13)+18; (2)(2.48)+4.33+(7.52)+(4.33);
(3) .
(1)原式15+18+(13)
33+(13) 20
(15+18)+(13)
加法交换律
加法结合律
符号相同的先结合
(2)原式(2.48)+(7.52)+(+4.33)+(4.33)
[(2.48)+(7.52)]+[(+4.33)+(4.33)]
(10)+0 10
能凑整的先凑整
互为相反数的先结合
解:
(3)原式=+
+(1)
分母相同的先结合
=
归纳总结
使用运算律通常有下列几种方法:
(1)能凑整的先凑整简称凑整结合法;
(2)把正数与负数分别结合在一起再相加简称同号结合法;
(3)有相反数的先把相反数相加简称相反数结合法;
(4)遇到分数,先把同分母的数相加,简称同分母结合法.
1、计算:
(1)5+(-7)+8
(2)(- )+ +(- )
(3)(-3.5)+[3+(-1.5)]
答案: 6
答案: -
答案: -2
课内练习
课内练习
2、用简便方法计算下列各题:
(1)14+(4)+(1)+16 +(5) (2)(18.65)+(7.25)+(+18.15)+(+7.25)
(3)(2.25)+(+(+(+0.125)
解:
(1)原式 (14+16)+[(4)+(1)+(5)] 30+(10) 20
(2)原式[(18.65)+(+18.15)]+[(7.25)+(+7.25)](0.5)+0 = 0.5
(3)原式 [(2.25)+() ]+[()+()] (3)+()
典例精析
例4: 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
你可以画一个示意图表示行驶过程吗?
思考1:
典例精析
思考2:
你可以列算式解决这个问题吗?
例4: 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
和方向有关
和方向无关
解:向东记为正,根据题意得:
(+15)+(25)+(+20)+(35)
=(15+20)+[(25)+(35)]
=25(m);
|+15|+|25|+|+20|+|35|
=15+25+20+35
=95(m).
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
同步训练
检修小组乘汽车沿公路检修线路(约定前进为正,后退为负),某天自A地出发到收工时所走的路程(单位:千米)为:11,-5,3,-4,8,14,-6,12,-9,6.
(1)收工时离A地有多少千米?
(2)若每千米耗油0.2升,则自A地出发到收工时共耗油多少升?
(1)11+(-5)+3+(-4)+8+14+(-6)+12+(-9)+6=30(千米).
答:收工时离A地有30千米.
(2)|+11|+|-5|+|+3|+|-4|+|+8|+|+14|+|-6|+|+12|+|-9|+|+6|
=78(千米).
78×0.2=15.6(升).
答:自A地出发到收工时共耗油15.6升.
解:
(2)任何两数相加,和不小于任何一个加数。
1. 数扩展到有理数之后,下面这些结论还成立吗?
请说明理由(如果认为结论不成立,请举例说明):
(1)若两个数的和是0,则这两个数都是0;
探究活动
不成立.例如:(3)+3=0,但30,30.
不唯一,互为相反数即可.
不成立.例如:10+()=3,但为3,小于加数10.
不唯一,异号相加即可.
课堂练习
1、7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应用了 ( )
A.加法交换律 B.加法结合律 C.分配律 D.加法交换律与结合律
D
2、下列交换加数的位置的变形中,错误的是 ( )
A.30+(-20)=(-20)+30 B.(-5)+(-13)=(-13)+(-5)
C.(-37)+16=16+(-37) D.10+(-20)=20+(-10)
3、计算6+(-3.5)+(+2.5)时,较好的方法是 ( )
A.按顺序进行计算 B.同号的数先相加
C.后面的两个数先相加 D.以上的方法都不对
D
C
4、若三个不相等的有理数的和为0,则下列结论正确的是 ( )
A. 三个数全是0 B. 至少有两个数是负数
C. 至少有一个数是负数 D. 至少有两个数是正数
C
5、用简便方法计算,并说明有关理由.
(1)12+(-18)+4;
(2)8+(-6)+5+(-8);
(3)(-2.4)+4.56+(-5.6)+(-4.56).
(2)原式=8+(-8)+(-6)+5=(-6)+5=-1.
解: (1)原式=12+4+(-18)=16+(-18)=-2.
(3)原式=[(-2.4)+(-5.6)]+[4.56+(-4.56)]=(-8)+0=-8.
6、有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,
则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6 +3 =300+3=303
答:这6筐蔬菜的总质量是303kg.
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
课堂总结
通过本节课的交流,你有什么体验或收获
一、加法的运算律
1、加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列几种方法:
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
作业布置
1.作业本
2.教材练习题
拓展提升
2、如图,在一个由6个圆圈组成的三角形里,将-15到-20这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和S都相等,那么S的最小值是 ( )
A. -53 B. -54 C. -56 D. -57
1、9个全不相等的有理数之和为0,这9个有理数中 ( )
A. 至少有一个为0 B. 至少有4个正数
C. 至少有一个负数 D. 至多有5个负数
C
B
趣味数学
“洛书”是世界上最古老的一个三阶幻方,它有三行三列,三横行的三个数之和、三竖列的三个数之和、两对角线的三个数之和都等于15.其实幻方就是把一些有规律且不相等的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等.如图,若将1~9填入幻方内,则a-b的值是________.
板书设计
2.1有理数的加法(2)
一、加法运算律
1、加法交换律:a+b=b+a
2、加法结合律: (a+b)+c=a+(b+c)
二、简便方法
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
