浙教版七年级上册2.2.1有理数的减法课件(共18张PPT)
文档属性
| 名称 | 浙教版七年级上册2.2.1有理数的减法课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览



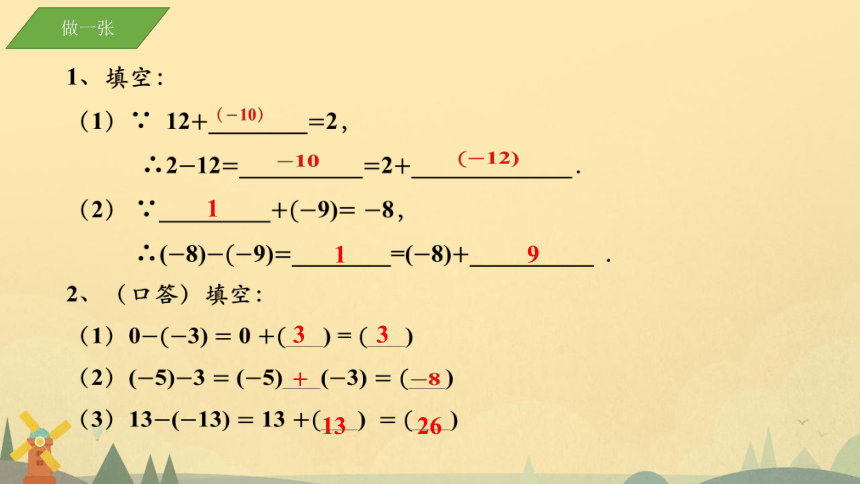


文档简介
(共18张PPT)
2.2有理数的减法(1)
情景导入
死海是世界著名的内陆咸水湖,湖水含盐量很高,人躺在水面上也不会下沉.死海海拔很低,其湖面低于海平面392米.我国吐鲁番盆地最低点的海拔为-154米,怎样比较两地海拔的差?
问题导入
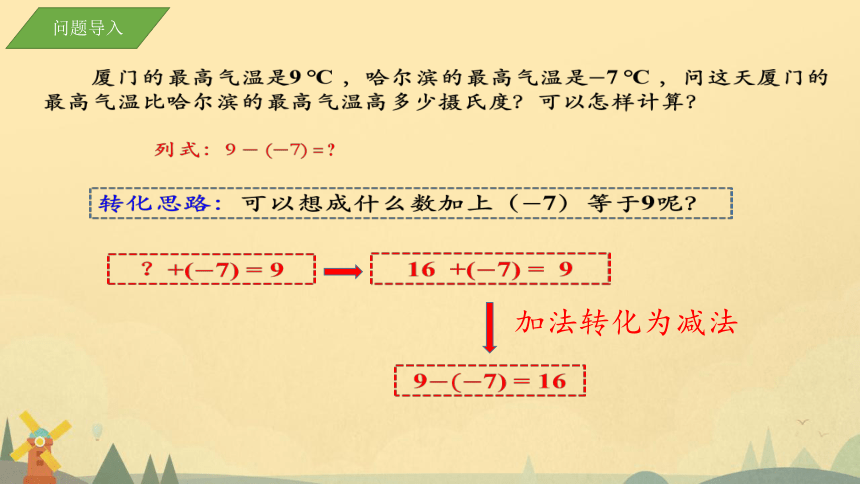
厦门的最高气温是9 ℃ ,哈尔滨的最高气温是7 ℃ ,问这天厦门的最高气温比哈尔滨的最高气温高多少摄氏度?可以怎样计算?
列式:9 (7)
转化思路:可以想成什么数加上(7)等于9呢?
?+(7) = 9
16 +(7) = 9
97) = 16
加法转化为减法
这三个式子有什么相同和不同的地方?
相 同
减 变 加
相 反 数
相 同
观察归纳
通过探究,你能概括出减法的计算法则吗
有理数的减法法则:
减去一个数,等于加上这个数的相反数。
ab
=
a(b)
注意:减法在运算时有 2个要素要发生变化.
1、减号
加号
它的相反数
2、减数
做一张
1、填空:
(1)∵ 12________2,
∴212__________2_____________.
(2) ∵_________9)8,
∴(8)9)________=(8)__________ .
(10)
10
12)
1
1
9
2、(口答)填空:
(1)03) 0 ) = )
(2)(5)3 (5) (3) )
(3)13(13) 13 ) )
+
3
8
3
13
26
典例精析
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
例1: 计算下列各题:
(1)55) (2)075 (3)(1.3)(2.1) (4)12
解:(1) 55) 5 5 = 10
(2)075 = 0(7)(5) = (7)+(5) = 12
(3)(1.3)(2.1) = (1.3)2.1 = 2.11.3 = 0.8
(4)12 12 1
做题时要依据法则
解法指导:
先把减法变加法,
再依加法法则计算.
减号变成加号
减数变成它的相反数
牛刀小试
(1)(+8) (+5)
(2)(+8) ( 5)
(3)( 8) ( 5)
(4)( 8) (+5)
(5)10 6
(6)6 10
= 3
= 13
= 3
= 13
= 4
= 4
减法不满足交换律
(7)( 2.5) 1.5
(8) ( )
(9)( 1) ( 4) 3
(10)( ) (+ )
(11)1 2
= 4
=
=
= 0
=
有理数减法与小学里学过的减法的不同点:
1、被减数可以小于减数.如: 1-5 ;
2、差可以大于被减数,如:(+3)-(-2) = 5;
3、大数减小数,差为正数;小数减大数,差为负数.
典例精析
例2 :我国吐鲁番盆地最低点的海拔高度是-155米,死海的湖面的海拔是-392米.哪里的海拔高度更低?低多少米?
(1)求低多少米,你认为是求哪两个数的差
(2)列算式时,哪个数作被减数,哪个数作减数
(3)怎样将减法转化为加法 哪个数变成它的相反数
(4)结果中的“”号的实际意义是什么
解:∵|392|>|155| ∴392<155 ∴死海的湖面更低
392 155) 392155 237(米).
答:死海的湖面更低,比吐鲁番盆地最低点低237米.
变式练习
2、以警戒线水位为基准,记高出警戒线水位为正.有一天长江某段水位高出警戒线1.8m,两天后水位下降了2m.问两天后水位高于或低于警戒线多少米?
解: (-2)-(+1.8)=(-2)+(-1.8)=-3.8(米)
答:两天后水位低于警戒线3.8米.
1、世界上最高的是珠穆朗玛峰,其海拔高度大约是8848米,吐鲁番盆地的海拔高度大约是-154米,两处高度相差多少米?
解:根据题意得:8848154) 8848+1 9002(米)
答:两处高度相差9002米.
课内练习
2、已知一个数与3的和是10,求这个数.
3、已知两数的和是最大的负整数,其中一个加数是最小的正整数,
求另一加数.
1、填空:
(1)(-7)-(-3)=(-7)+________=________;
(2)(-5)-4=(-5)+________=________;
(3)0-(-2.5)=0+________=________.
3
4
(4)
9
2.5
2.5
3 10
10 – 3 = 10(– 3) = (10+3) = 13
最大的负整数:1
最小的正整数:1
1
1 – 1 = 1(– 1) = (1+1) =
深化拓展
在数轴上,点A,B,C,D表示的有理数分别是+1,+5, 2, 3.
请问以下两点间的距离是多少?
(1)A,B两点:
(2)C,D两点:
(3)A,D两点:
4个单位
1个单位
4个单位
=5 1
= 2 ( 3)
=1 ( 3)
=|1 5|
=| 3 ( 2)|
=|( 3) 1|
0
1
2
3
4
1
2
3
4
5
5
A
B
C
D
数轴上两点间距离=大 小
=|小 大|
数轴上表示数a和b的两点间的距离=
|a b|
∴|a b|的几何意义是数轴上表示数a的点到表示数b的点之间的距离.
方法一:思考:|a 3|=5的几何意义是什么?
数轴上表示a的点到3的距离等于5.
3
4
5
6
7
2
1
0
1
8
2
5个单位
5个单位
方法二:思考: ①什么数的绝对值等于5?
a= 2或8
②这题中谁等于±5?
±5
a 3=±5
即 a 3=5或a 3= 5
∴a=8或 2.
变式练习:根据上述方法,请思考:若|b+2|=4,则b=___________.
2或6
深化拓展
当堂检测
1、下列说法是否正确.
(1)零减去一个数,仍得这个数. ( )
(2)正数减去正数,仍得正数. ( )
(3)负数减去正数,结果是负数. ( )
(4)被减数一定大于差. ( )
(5)若两数和为零,则这两数都为零. ( )
(6)任何两数相加,和不小于加数. ( )
2、下列说法正确的是 ( )
(A)减去一个负数,差一定大于被减数
(C)减去一个正数,差不一定大于被减数
(B)0减去任何数,差都是负数
(D)两个数之差一定小于被减数
A
3、点A,B,C在同一条数轴上,其中点A,B表示的数分别为-3,1.若点B,C之间
的距离为2,则点A,C之间的距离为 ( )
A. 3 B. 2 C. 3或5 D. 2或6
D
4、计算:
(1)(-5)-(+1)-(-6);
解:(1)原式 = (-6)-(-6) = (-6)+6 = 0.
(2)原式 = 20-(+3) = 17.
(3)原式 = -1-9 = -10.
(2)11-(-9)-(+3);
(3)-6-(-5)-9.
5、列式计算:
(1)和是-2,一个加数是6,求另一个加数.(2)4与-3的差的相反数.
解:(1)-2-6=-8. (2)-[4-(-3)]=-(4+3)=-7.
6、已知|a|=4,|b|=6.若|a+b|=-(a+b),求a-b的值.
解: ∵|a|=4,|b|=6,|a+b|=-(a+b),∴a=4,b=-6或a=-4,b=-6,
∴当a=4,b=-6时,a-b=4-(-6)=4+6=10;
当a=-4,b=-6时,a-b=(-4)-(-6)=(-4)+6=2.
综上所述,a-b的值为10或2.
通过本节课的交流,你有什么体验或收获
课堂总结
1.有理数减法法则:
减去一个数,等于加上这个数的相反数.
2.减法转化成加法时应注意:
减号变加号,减数变相反数.
两处同时改变符号.
3.有理数减法与小学里学过的减法的不同点:
被减数可以小于减数.如: 1-5 ;
差可以大于被减数,如:(+3)-(-2) = 5;
大数减小数,差为正数;小数减大数,差为负数.
4.|a b|的几何意义:数轴上表示数a的点到表示数b的点之间的距离.
1.作业本
2.校本作业
作业布置
拓展提升
点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|ab|.回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示2和3的两点之间的距离是 ;
(2)数轴上表示x和2的两点之间的距离为 ;
(3)若x表示一个有理数,且4≤x≤2,则|x2||x4|= ;
(4)若|x3||x5|=8,求出x的整数值.
解:(1) 52=3,2(3)5.故答案为3,5.
(2) |x2|.
(3) 6.
(4)因为|x3||x5|8,所以3≤x≤5,所以x的整数值为3,2,1,0,1,2,3,4,5.
趣味数学
2.2有理数的减法(1)
情景导入
死海是世界著名的内陆咸水湖,湖水含盐量很高,人躺在水面上也不会下沉.死海海拔很低,其湖面低于海平面392米.我国吐鲁番盆地最低点的海拔为-154米,怎样比较两地海拔的差?
问题导入
厦门的最高气温是9 ℃ ,哈尔滨的最高气温是7 ℃ ,问这天厦门的最高气温比哈尔滨的最高气温高多少摄氏度?可以怎样计算?
列式:9 (7)
转化思路:可以想成什么数加上(7)等于9呢?
?+(7) = 9
16 +(7) = 9
97) = 16
加法转化为减法
这三个式子有什么相同和不同的地方?
相 同
减 变 加
相 反 数
相 同
观察归纳
通过探究,你能概括出减法的计算法则吗
有理数的减法法则:
减去一个数,等于加上这个数的相反数。
ab
=
a(b)
注意:减法在运算时有 2个要素要发生变化.
1、减号
加号
它的相反数
2、减数
做一张
1、填空:
(1)∵ 12________2,
∴212__________2_____________.
(2) ∵_________9)8,
∴(8)9)________=(8)__________ .
(10)
10
12)
1
1
9
2、(口答)填空:
(1)03) 0 ) = )
(2)(5)3 (5) (3) )
(3)13(13) 13 ) )
+
3
8
3
13
26
典例精析
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
例1: 计算下列各题:
(1)55) (2)075 (3)(1.3)(2.1) (4)12
解:(1) 55) 5 5 = 10
(2)075 = 0(7)(5) = (7)+(5) = 12
(3)(1.3)(2.1) = (1.3)2.1 = 2.11.3 = 0.8
(4)12 12 1
做题时要依据法则
解法指导:
先把减法变加法,
再依加法法则计算.
减号变成加号
减数变成它的相反数
牛刀小试
(1)(+8) (+5)
(2)(+8) ( 5)
(3)( 8) ( 5)
(4)( 8) (+5)
(5)10 6
(6)6 10
= 3
= 13
= 3
= 13
= 4
= 4
减法不满足交换律
(7)( 2.5) 1.5
(8) ( )
(9)( 1) ( 4) 3
(10)( ) (+ )
(11)1 2
= 4
=
=
= 0
=
有理数减法与小学里学过的减法的不同点:
1、被减数可以小于减数.如: 1-5 ;
2、差可以大于被减数,如:(+3)-(-2) = 5;
3、大数减小数,差为正数;小数减大数,差为负数.
典例精析
例2 :我国吐鲁番盆地最低点的海拔高度是-155米,死海的湖面的海拔是-392米.哪里的海拔高度更低?低多少米?
(1)求低多少米,你认为是求哪两个数的差
(2)列算式时,哪个数作被减数,哪个数作减数
(3)怎样将减法转化为加法 哪个数变成它的相反数
(4)结果中的“”号的实际意义是什么
解:∵|392|>|155| ∴392<155 ∴死海的湖面更低
392 155) 392155 237(米).
答:死海的湖面更低,比吐鲁番盆地最低点低237米.
变式练习
2、以警戒线水位为基准,记高出警戒线水位为正.有一天长江某段水位高出警戒线1.8m,两天后水位下降了2m.问两天后水位高于或低于警戒线多少米?
解: (-2)-(+1.8)=(-2)+(-1.8)=-3.8(米)
答:两天后水位低于警戒线3.8米.
1、世界上最高的是珠穆朗玛峰,其海拔高度大约是8848米,吐鲁番盆地的海拔高度大约是-154米,两处高度相差多少米?
解:根据题意得:8848154) 8848+1 9002(米)
答:两处高度相差9002米.
课内练习
2、已知一个数与3的和是10,求这个数.
3、已知两数的和是最大的负整数,其中一个加数是最小的正整数,
求另一加数.
1、填空:
(1)(-7)-(-3)=(-7)+________=________;
(2)(-5)-4=(-5)+________=________;
(3)0-(-2.5)=0+________=________.
3
4
(4)
9
2.5
2.5
3 10
10 – 3 = 10(– 3) = (10+3) = 13
最大的负整数:1
最小的正整数:1
1
1 – 1 = 1(– 1) = (1+1) =
深化拓展
在数轴上,点A,B,C,D表示的有理数分别是+1,+5, 2, 3.
请问以下两点间的距离是多少?
(1)A,B两点:
(2)C,D两点:
(3)A,D两点:
4个单位
1个单位
4个单位
=5 1
= 2 ( 3)
=1 ( 3)
=|1 5|
=| 3 ( 2)|
=|( 3) 1|
0
1
2
3
4
1
2
3
4
5
5
A
B
C
D
数轴上两点间距离=大 小
=|小 大|
数轴上表示数a和b的两点间的距离=
|a b|
∴|a b|的几何意义是数轴上表示数a的点到表示数b的点之间的距离.
方法一:思考:|a 3|=5的几何意义是什么?
数轴上表示a的点到3的距离等于5.
3
4
5
6
7
2
1
0
1
8
2
5个单位
5个单位
方法二:思考: ①什么数的绝对值等于5?
a= 2或8
②这题中谁等于±5?
±5
a 3=±5
即 a 3=5或a 3= 5
∴a=8或 2.
变式练习:根据上述方法,请思考:若|b+2|=4,则b=___________.
2或6
深化拓展
当堂检测
1、下列说法是否正确.
(1)零减去一个数,仍得这个数. ( )
(2)正数减去正数,仍得正数. ( )
(3)负数减去正数,结果是负数. ( )
(4)被减数一定大于差. ( )
(5)若两数和为零,则这两数都为零. ( )
(6)任何两数相加,和不小于加数. ( )
2、下列说法正确的是 ( )
(A)减去一个负数,差一定大于被减数
(C)减去一个正数,差不一定大于被减数
(B)0减去任何数,差都是负数
(D)两个数之差一定小于被减数
A
3、点A,B,C在同一条数轴上,其中点A,B表示的数分别为-3,1.若点B,C之间
的距离为2,则点A,C之间的距离为 ( )
A. 3 B. 2 C. 3或5 D. 2或6
D
4、计算:
(1)(-5)-(+1)-(-6);
解:(1)原式 = (-6)-(-6) = (-6)+6 = 0.
(2)原式 = 20-(+3) = 17.
(3)原式 = -1-9 = -10.
(2)11-(-9)-(+3);
(3)-6-(-5)-9.
5、列式计算:
(1)和是-2,一个加数是6,求另一个加数.(2)4与-3的差的相反数.
解:(1)-2-6=-8. (2)-[4-(-3)]=-(4+3)=-7.
6、已知|a|=4,|b|=6.若|a+b|=-(a+b),求a-b的值.
解: ∵|a|=4,|b|=6,|a+b|=-(a+b),∴a=4,b=-6或a=-4,b=-6,
∴当a=4,b=-6时,a-b=4-(-6)=4+6=10;
当a=-4,b=-6时,a-b=(-4)-(-6)=(-4)+6=2.
综上所述,a-b的值为10或2.
通过本节课的交流,你有什么体验或收获
课堂总结
1.有理数减法法则:
减去一个数,等于加上这个数的相反数.
2.减法转化成加法时应注意:
减号变加号,减数变相反数.
两处同时改变符号.
3.有理数减法与小学里学过的减法的不同点:
被减数可以小于减数.如: 1-5 ;
差可以大于被减数,如:(+3)-(-2) = 5;
大数减小数,差为正数;小数减大数,差为负数.
4.|a b|的几何意义:数轴上表示数a的点到表示数b的点之间的距离.
1.作业本
2.校本作业
作业布置
拓展提升
点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|ab|.回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示2和3的两点之间的距离是 ;
(2)数轴上表示x和2的两点之间的距离为 ;
(3)若x表示一个有理数,且4≤x≤2,则|x2||x4|= ;
(4)若|x3||x5|=8,求出x的整数值.
解:(1) 52=3,2(3)5.故答案为3,5.
(2) |x2|.
(3) 6.
(4)因为|x3||x5|8,所以3≤x≤5,所以x的整数值为3,2,1,0,1,2,3,4,5.
趣味数学
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
