2.4二次函数的应用（1）

课件14张PPT。2.4 二次函数的应用⑴温故知新：1、二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值？2、如何求二次函数的最值？配方法公式法3、求下列函数的最大值或最小值：
①y=x2-4x+7 ②y=-5x2+8x-1配方法公式法问题1:给你长8m的铝合金条，设问：
①你能用它制成一矩形窗框吗？②怎样设计，窗框的透光面积最大？ 运用二次函数求实际问题中的最大值或
最小值解题的一般步骤是怎样的？1.求出函数解析式3.通过配方变形，
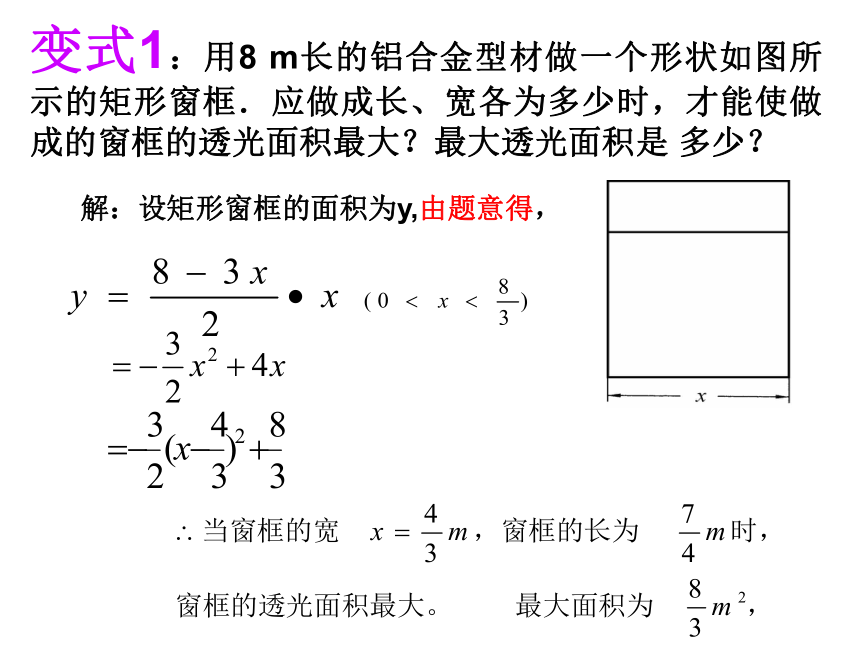
或利用公式求它的最大值或最小值。2.求出自变量的取值范围注意：由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内。变式1：用8 m长的铝合金型材做一个形状如图所示的矩形窗框．应做成长、宽各为多少时，才能使做成的窗框的透光面积最大？最大透光面积是 多少？解：设矩形窗框的面积为y,由题意得，变式2:图中窗户边框的上半部分是由四个全等扇形组成的半圆，下部分是矩形。如果制作一个窗户边框的材料总长为6米，那么如何设计这个窗户边框的尺寸，使透光面积最大(结果精确到0.01m2)?
xy解:设半圆的半径为x米，如图，矩形的一边长为y米，根据题意，有5x+πx+2x+2y=6,即：y=3－0.5(π+7)x∵ y＞0且x ＞0∴3－0.5(π+7)x＞0∵ a≈-8.57＜0，b=6，c=0≈1.05此时y≈1.23答：当窗户半圆的半径约为0.35m，矩形窗框的一边长约为1.23m时，窗户的透光面积最大，最大值为1.05m2。xy2x问题2:用长为8米的铝合金制成如图窗框，一边靠2m的墙，问窗框的宽和高各为多少米时，窗户的透光面积最大？最大面积是多少？x8-2x小结：应用二次函数的性质解决日常生活中的最值问题，一般的步骤为：①把问题归结为二次函数问题（设自变量和函数）；②求出函数解析式（包括自变量的取值范围）；③在自变量的取值范围内求出最值；
（数形结合找最值）④答。数学建模做一做 如图，隧道横截面的下部是矩形，上部是半圆，周长为16米。
⑴求截面积S（米2）关于底部宽x（米）的函数解析式，及自变量x 的取值范围？⑵试问：当底部宽x为几米时，隧道的截面积S最大（结果精确到0.01米）？解：∵隧道的底部宽为x，周长为16，答：当隧道的底部宽度为4.48米时，隧道的截面积最大。收获：学了今天的内容，我们意识到所学的数学是有用的，巧妙地应用数学知识可以解决生活中碰到的很多问题！实际问题抽象转化数学问题运用数学知识返回解释检验问题的解如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。解： (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米 (3) ∵墙的可用长度为8米∴ S＝x（24－4x）
＝－4x2＋24 x （0生活中处处有数学，
就看我们怎么用它了……再见