2.7探索勾股定理（2）

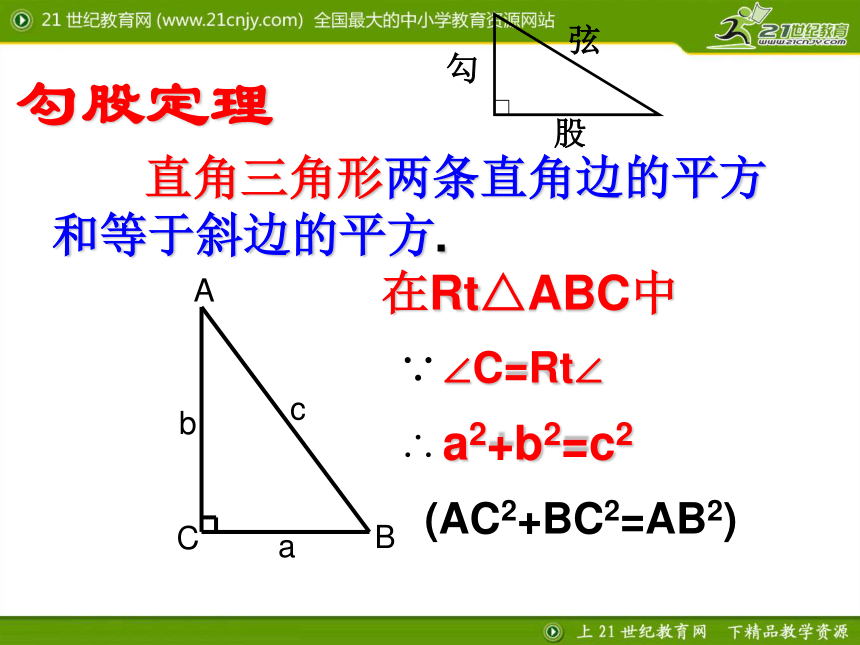
课件16张PPT。2.7 探索勾股定理（2)1、在直角三角形ABC中,∠C=90°，（１）已知ａ：ｂ＝３：４，ｃ＝２５，求ａ和ｂ（２）已知∠Ａ＝３０°ａ＝３，求ｂ和ｃ２、直角△的两边长为８和１０，求第三边的长度．复习回顾勾股定理 直角三角形两条直角边的平方
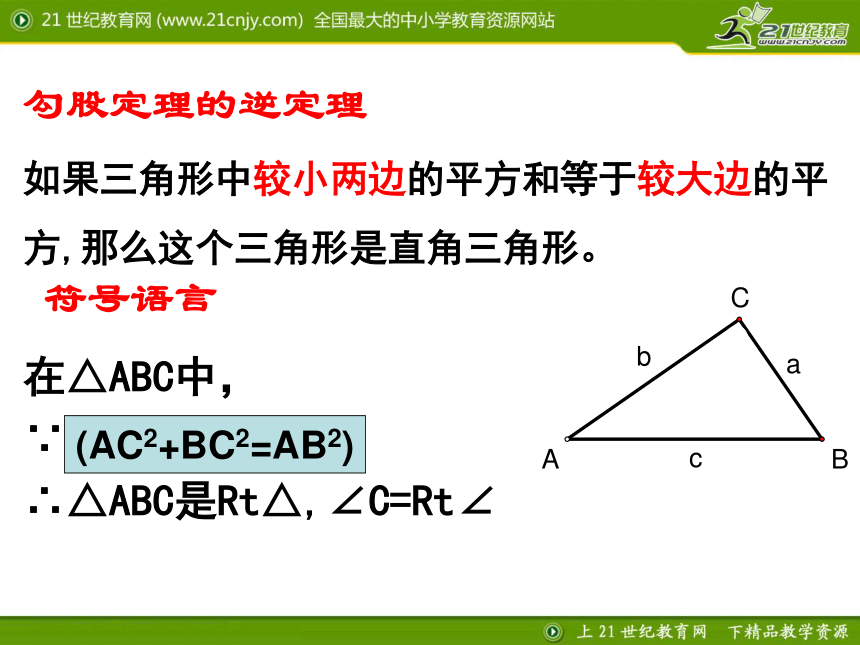
和等于斜边的平方.∴ a2+b2=c2在Rt△ABC中∵ ∠C=Rt∠(AC2+BC2=AB2)勾股弦 古埃及人曾用下面的方法得到直角：如图所示，他们用13个等距的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第一个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处。合作学习(1)画一个三角形,使其三边长分别为: a=3cm，b=4cm，c=5cm.如果三角形中较小两边的平方和等于较大边的平方,那么这个三角形是直角三角形。符号语言在△ABC中，
∵a2+b2=c2（已知）
∴△ABC是Rt△,∠C=Rt∠ 勾股定理的逆定理(AC2+BC2=AB2)1.想一想:上述哪条边所对的角是直角?2.这个定理可判断三角形是否是直角三角形.3.能够成为直角三角形三边长的三个正整数，称为勾股数（或勾股弦数）。 如3、4、5；6、8、10；5、12、13。 1.若一个三角形的三边满足a2-b2=c2 ,则这个三角形为（ ）
A：直角三角形 B：正三角形
C：锐角三角形 D：钝角三角形
2.在△ABC中BC＝a,AC＝b,AB＝c,且b2＋c2=a2, 则∠ ＝90°
巩固新知，加以应用例１．根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形．
　 (1) a=8,b=15,c=17.
(2) a:b:c= : :2
练一练 根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形．
　 (1) a= , b=1,c=3;
(2) a:b:c=3: : ;
例2.已知ΔABC的三条边长分别为a、b、c,且a= - ,b=2mn, c= + (m>n,m,n是正整数).三角形是直角三角形吗?请说明理由.例3：如图，在四边形ABCD中,AB=3,BC=4, CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
练一练 如图，在四边形ABCD中,AB=4,BC=3, CD=12,AD=13,∠B=90°,求四边形ABCD的面积.割补法3413121、在△ABC中,AD=9,DB=3,CD= ,CB=6.找出图中所有的直角三角形,并说明理由.综合练习勾股定理的逆定理：如果三角形中较小两边的平方和等于较大边的平方,那么这个三角形是直角三角形。符号语言在△ABC中，
∵a2+b2=c2
∴△ABC是Rt△AC2+BC2=AB2理一理适度拓展1、如图，在正方形ABCD中，F为DC的中点，E为BC上一点，且EC= BC，
那么AF⊥EF.试说明理由.如图中分别以△ABC三边a,b,c为边向外作正方形,正三角形,为直径作半圆.若S1+S2=S3成立,则△ABC是直角三角形吗？acb书P43阅读材料：