第3章 圆周角定理、圆内接四边形 单元测试(Word版,无答案)
文档属性
| 名称 | 第3章 圆周角定理、圆内接四边形 单元测试(Word版,无答案) | 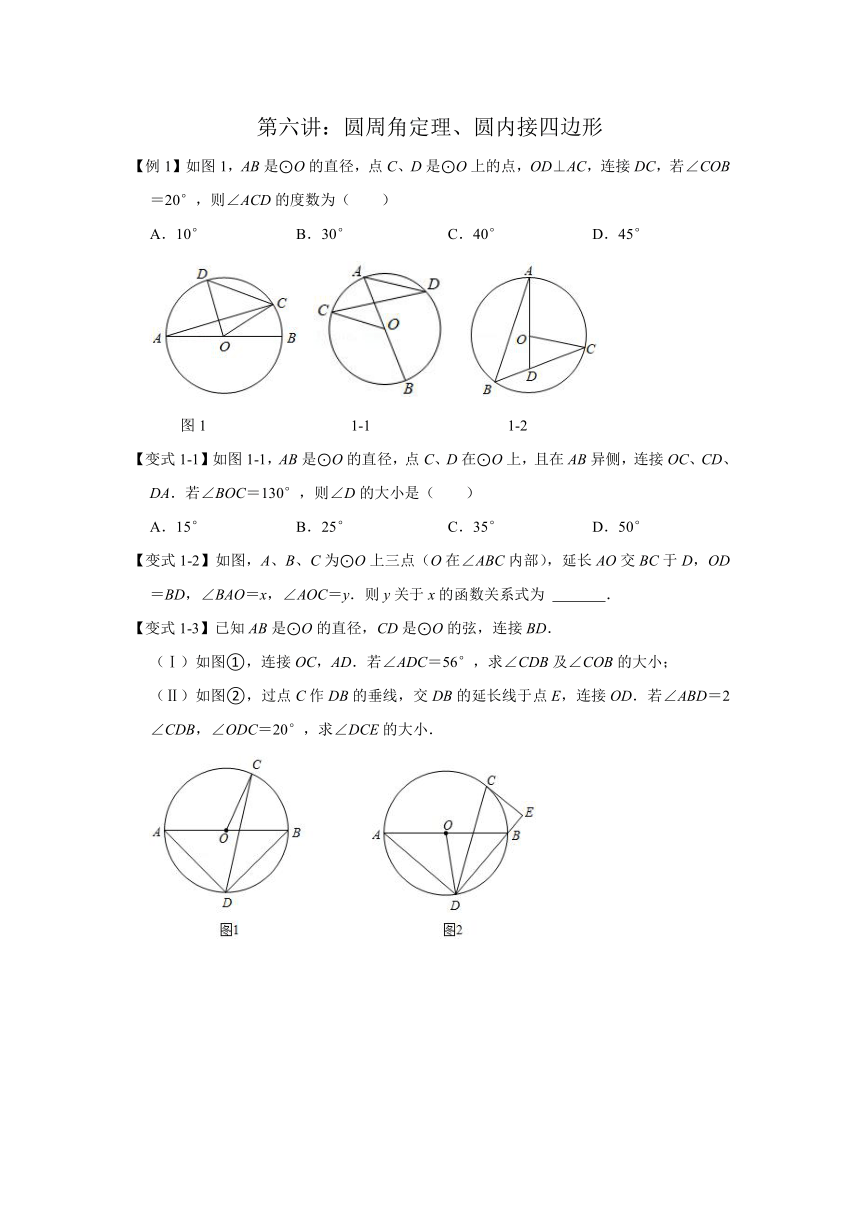 | |
| 格式 | docx | ||
| 文件大小 | 126.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 16:19:05 | ||
图片预览

文档简介
第六讲:圆周角定理、圆内接四边形
【例1】如图1,AB是⊙O的直径,点C、D是⊙O上的点,OD⊥AC,连接DC,若∠COB=20°,则∠ACD的度数为( )
A.10° B.30° C.40° D.45°
图1 1-1 1-2
【变式1-1】如图1-1,AB是⊙O的直径,点C、D在⊙O上,且在AB异侧,连接OC、CD、DA.若∠BOC=130°,则∠D的大小是( )
A.15° B.25° C.35° D.50°
【变式1-2】如图,A、B、C为⊙O上三点(O在∠ABC内部),延长AO交BC于D,OD=BD,∠BAO=x,∠AOC=y.则y关于x的函数关系式为 .
【变式1-3】已知AB是⊙O的直径,CD是⊙O的弦,连接BD.
(Ⅰ)如图①,连接OC,AD.若∠ADC=56°,求∠CDB及∠COB的大小;
(Ⅱ)如图②,过点C作DB的垂线,交DB的延长线于点E,连接OD.若∠ABD=2∠CDB,∠ODC=20°,求∠DCE的大小.
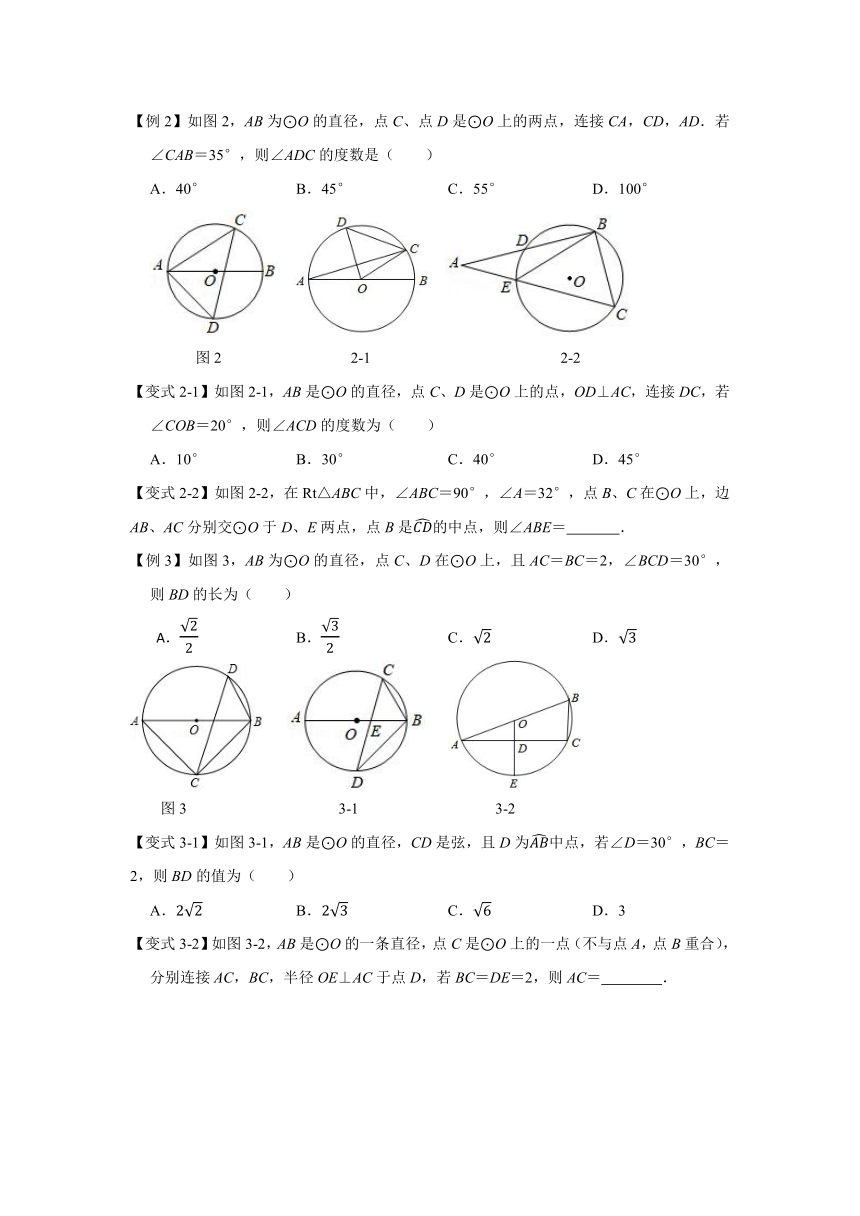
【例2】如图2,AB为⊙O的直径,点C、点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=35°,则∠ADC的度数是( )
A.40° B.45° C.55° D.100°
图2 2-1 2-2
【变式2-1】如图2-1,AB是⊙O的直径,点C、D是⊙O上的点,OD⊥AC,连接DC,若∠COB=20°,则∠ACD的度数为( )
A.10° B.30° C.40° D.45°
【变式2-2】如图2-2,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在⊙O上,边AB、AC分别交⊙O于D、E两点,点B是的中点,则∠ABE= .
【例3】如图3,AB为⊙O的直径,点C、D在⊙O上,且AC=BC=2,∠BCD=30°,则BD的长为( )
B. C. D.
图3 3-1 3-2
【变式3-1】如图3-1,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
【变式3-2】如图3-2,AB是⊙O的一条直径,点C是⊙O上的一点(不与点A,点B重合),分别连接AC,BC,半径OE⊥AC于点D,若BC=DE=2,则AC= .
【例4】如图4,AB是⊙O的直径,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①至少存在一点P,使得PA>AB; ②若2,则PB=2PA;
③∠PAB不是直角; ④∠POB=2∠OPA.
上述结论中,所有正确结论的序号是 .
图4 图4-1 图4-2
【变式4-1】如图4-1所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且,连接CM,交AB于点E,交AN于点F,现给出以下结论:①∠MAN=90°;②;③∠ACM+∠ANM=∠MOB;④AEMF,其中正确结论的序号是 .
【变式4-2】如图4-2,AB是⊙O的直径,AB=AC,BC交⊙O于点E,∠BAC=45°,给出下列四个结论:①∠EBC=22.5°②BD=DC③AE=DC④2,其中正确结论有 (只填序号)
【例5】如图5,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,E为线段CD上一个动点,连接OE,则OE的最小值为 .
图5
【变式5-1】如图,△ABC中,∠BAC=60°,∠ABC=45°,D是边BC上(不与端点重合)的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,若线段AD长度的最小值为,则线段EF长度的最小值为 .
【例6】如图6,四边形ABCD内接于⊙O,连接AC、BD,若AC=AD,∠CBE=70°,则∠DBC= .
图6 6-1
【变式6-1】如图6-1,四边形ABCD内接于⊙O,DA=DC,若∠CBE=55°,则∠DAC的度数为( )
A.70° B.67.5° C.62.5° D.65°
【变式6-2】已知:如图,四边形ABCD内接于⊙O,DB=DC.求证:AD平分∠EAC.
【例1】如图1,AB是⊙O的直径,点C、D是⊙O上的点,OD⊥AC,连接DC,若∠COB=20°,则∠ACD的度数为( )
A.10° B.30° C.40° D.45°
图1 1-1 1-2
【变式1-1】如图1-1,AB是⊙O的直径,点C、D在⊙O上,且在AB异侧,连接OC、CD、DA.若∠BOC=130°,则∠D的大小是( )
A.15° B.25° C.35° D.50°
【变式1-2】如图,A、B、C为⊙O上三点(O在∠ABC内部),延长AO交BC于D,OD=BD,∠BAO=x,∠AOC=y.则y关于x的函数关系式为 .
【变式1-3】已知AB是⊙O的直径,CD是⊙O的弦,连接BD.
(Ⅰ)如图①,连接OC,AD.若∠ADC=56°,求∠CDB及∠COB的大小;
(Ⅱ)如图②,过点C作DB的垂线,交DB的延长线于点E,连接OD.若∠ABD=2∠CDB,∠ODC=20°,求∠DCE的大小.
【例2】如图2,AB为⊙O的直径,点C、点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=35°,则∠ADC的度数是( )
A.40° B.45° C.55° D.100°
图2 2-1 2-2
【变式2-1】如图2-1,AB是⊙O的直径,点C、D是⊙O上的点,OD⊥AC,连接DC,若∠COB=20°,则∠ACD的度数为( )
A.10° B.30° C.40° D.45°
【变式2-2】如图2-2,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在⊙O上,边AB、AC分别交⊙O于D、E两点,点B是的中点,则∠ABE= .
【例3】如图3,AB为⊙O的直径,点C、D在⊙O上,且AC=BC=2,∠BCD=30°,则BD的长为( )
B. C. D.
图3 3-1 3-2
【变式3-1】如图3-1,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
【变式3-2】如图3-2,AB是⊙O的一条直径,点C是⊙O上的一点(不与点A,点B重合),分别连接AC,BC,半径OE⊥AC于点D,若BC=DE=2,则AC= .
【例4】如图4,AB是⊙O的直径,点P是⊙O上一个动点(点P不与点A,B重合),在点P运动的过程中,有如下四个结论:
①至少存在一点P,使得PA>AB; ②若2,则PB=2PA;
③∠PAB不是直角; ④∠POB=2∠OPA.
上述结论中,所有正确结论的序号是 .
图4 图4-1 图4-2
【变式4-1】如图4-1所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且,连接CM,交AB于点E,交AN于点F,现给出以下结论:①∠MAN=90°;②;③∠ACM+∠ANM=∠MOB;④AEMF,其中正确结论的序号是 .
【变式4-2】如图4-2,AB是⊙O的直径,AB=AC,BC交⊙O于点E,∠BAC=45°,给出下列四个结论:①∠EBC=22.5°②BD=DC③AE=DC④2,其中正确结论有 (只填序号)
【例5】如图5,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,E为线段CD上一个动点,连接OE,则OE的最小值为 .
图5
【变式5-1】如图,△ABC中,∠BAC=60°,∠ABC=45°,D是边BC上(不与端点重合)的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,若线段AD长度的最小值为,则线段EF长度的最小值为 .
【例6】如图6,四边形ABCD内接于⊙O,连接AC、BD,若AC=AD,∠CBE=70°,则∠DBC= .
图6 6-1
【变式6-1】如图6-1,四边形ABCD内接于⊙O,DA=DC,若∠CBE=55°,则∠DAC的度数为( )
A.70° B.67.5° C.62.5° D.65°
【变式6-2】已知:如图,四边形ABCD内接于⊙O,DB=DC.求证:AD平分∠EAC.
同课章节目录
