2.1.2有理数的加法 课件
图片预览





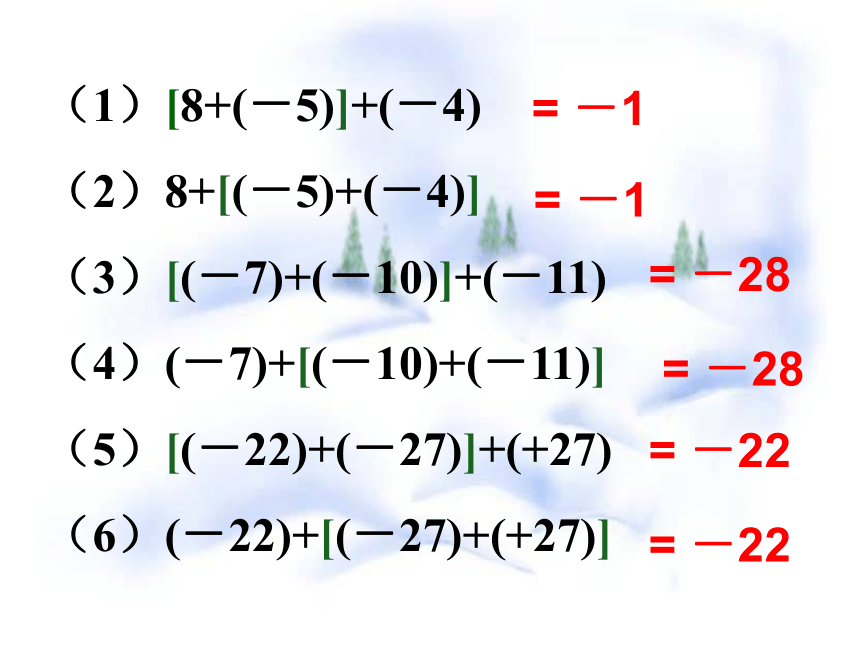


文档简介
课件28张PPT。2.1.2 有理数的加法1.同号两数相加,取与加数相同的符号,并把绝对值相加。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
3.互为相反数的两个数相加得0。
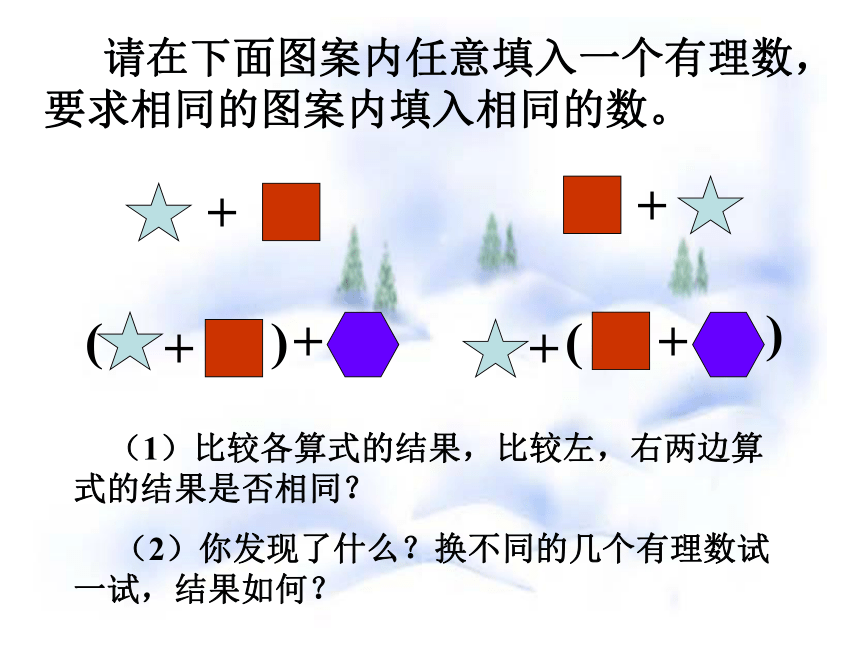
一个数同0相加,仍得这个数。有理数加法法则运算步骤再确定和的符号;后进行绝对值的加减运算先判断类型(同号、异号等);++++()++() 请在下面图案内任意填入一个有理数,要求相同的图案内填入相同的数。 (1)比较各算式的结果,比较左,右两边算式的结果是否相同?
(2)你发现了什么?换不同的几个有理数试一试,结果如何?(1)(-9.18)+6.18
(2)6.18+(-9.18)
(3)(-2.37)+(-4.63)
(4)(-4.63)+(-2.37)计算并观察= -3= -3= -7= -7加法交换律:两个数相加,交 换加数的位置,和不变a+b=b+a(1)[8+(-5)]+(-4)
(2)8+[(-5)+(-4)]
(3)[(-7)+(-10)]+(-11)
(4)(-7)+[(-10)+(-11)]
(5)[(-22)+(-27)]+(+27)
(6)(-22)+[(-27)+(+27)]= -1= -1= -28= -28= -22= -22加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变(a+b)+c=a+(b+c)一般地,任意若干个数相加,无论各
数相加的先后次序如何,其和都不变。a+b=b+a
例(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)计算例1、计算:(1) 15+(-13)+18(2) (-2.48)+4.33+(-7.52)+(-4.33)(3)15+18+(-13)=(15+18)+(-13)=33+(-13)=20解:(-2.48)+(-7.52)+4.33+(-4.33)=[(-2.48)+(-7.52)]+[4.33+(-4.33)]=(-10)+0=-10解:注意解题格式!解:使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。解题策略1、计算:
(1)5+(-7) +8
(2)
(3)(-3.5)+[3+(-1.5)]=5+8+(-7)=(5+8)+7=6=(-3.5)+(-1.5)+3 =[(-3.5)+(-1.5)]+3=-2用简便方法计算,并说明相关理由1)2)3)行家看“门道”例2、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15米,再向西行驶25米,然后又向东行驶20米,再向西行驶35米,问玩具赛车最后停在何处?一共行驶了多少米? -5-15-20-10051015-25西东A15-3520-25行家看“门道”例2、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15米,再向西行驶25米,然后又向东行驶20米,再向西行驶35米,问玩具赛车最后停在何处?一共行驶了多少米? 解:规定向东行驶为正,则
(+15)+(-25)+(+20)+(-35)=[(+15)+(+20)]+[(-25)+(-35)]=(+35)+(-60)=-25(米)
一共行驶的路程为|+15|+|-25|+|+20|+|-35|=95(米)
答:玩具赛车最后停在A地向西25米处,一共行驶了95米。 练习1:某升降机第一次上升8米,第二次又上升6米,第三次下降7米,第四次又下降了9米,这时升降机在初始位置的什么位置?升降机共运行了多少米?2. 蚂蚁从某点O出发在一条直线上来回爬行,假定向右爬行的路程为正数,向左爬行的路程为负数,爬过的各段路程依次为(单位:厘米)
+6,-3,+10,-5,-7,+13,-10
(1)蚂蚁最后是否回到了出发点?
(2)蚂蚁离开出发点O最远是多少厘米?
(3)在爬行过程中,如果爬行1厘米奖励一粒芝麻,则蚂蚁一共得到多少粒芝麻?小明记录了一星期每天的最低温度如下表:这个星期的平均最低温度是多少摄氏度?
平均最低温度=
最低温度之和
天数 数扩展到有理数后,下面这些结论还成立吗?请说明理由(如果认为结论不正确,请举例说明):
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数; ××(1)把正数和负数分别结合在一起相加(2)把互为相反数的结合,能凑整的结合(3)把同分母的数结合相加1.有理数加法交换律和结合律这一节课学习了什么内容?你学会了吗?2.运用加法交换律和结合律要注意:3.运算律的作用能使运算简便 用“﹥”或“﹤”符号填空
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a<0,b>0,|a|<|b|,那么a+b____0;
探究如图,在钟面上有12个数字,如果在某些数前添上负号,可以使12个数字之和等于0,例如,-1+2+(-3)+4+(-5)+6+7+(-8)+9+
(-10)+11+(-12)=0;(1)请你再写出一种添加负号的方法;(2)想一想,这样的负号至少需添加几个?请举例说明.(3)以上解题过程中,你是怎样想的?开放题1、有下列说法:
(1)若干个有理数相加,和必大于任一个 加数。 (2)3个有理数相加,其和不可能为零。(3)若干个有理数相加的和仍然是有理数。 (4)两个有理数的和不大于两个有理数的绝对值的和。
其中正确的有几个?拓展练习:2、计算:
(-1)+2+(-3)+4+(-5)+6+(-7)+……+(-2011)+2012+(-2013)3、绝对值大于5,但不大于8的所有整数的和是多少?4、把6个圆圈排成如图所示的三角形,每边三个圆圈,把数字-7,-3,1,5,9,13分别填在这6个圆圈中,使各边上的数字之和相等。请填出符合条件的填法。5、若a+b+c=0,且b<c<0,
则下列结论正确的有几个:
(1)a+b>0;(2)b+c <0;
(3)c+a >0;(4)a-c <06、代数式 能取的最小值为多
少?此时x的值是多少?8、若a、b、c、d是互不相等的整数,且abcd=9,那么a+b+c+d等于多少?9、设三个互不相等的有理数,既可表示成1、a+b、a的形式,有可表示成0、a/b、b的形式,试求a2+b3的值。10、观察两个算式并回答问题:
算式:(1)63×67=6×(6+1)×100+3×7=4200+21=4221
(2)692×698=69×(69+1)×100+2×8=483000+16=483016
问题(1)两个因数各位上数字之和是多少?其余各位上的数字有什么特征?
(2)根据计算,猜想并举例验证符合上述特征的两数相乘的运算法则。
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
3.互为相反数的两个数相加得0。
一个数同0相加,仍得这个数。有理数加法法则运算步骤再确定和的符号;后进行绝对值的加减运算先判断类型(同号、异号等);++++()++() 请在下面图案内任意填入一个有理数,要求相同的图案内填入相同的数。 (1)比较各算式的结果,比较左,右两边算式的结果是否相同?
(2)你发现了什么?换不同的几个有理数试一试,结果如何?(1)(-9.18)+6.18
(2)6.18+(-9.18)
(3)(-2.37)+(-4.63)
(4)(-4.63)+(-2.37)计算并观察= -3= -3= -7= -7加法交换律:两个数相加,交 换加数的位置,和不变a+b=b+a(1)[8+(-5)]+(-4)
(2)8+[(-5)+(-4)]
(3)[(-7)+(-10)]+(-11)
(4)(-7)+[(-10)+(-11)]
(5)[(-22)+(-27)]+(+27)
(6)(-22)+[(-27)+(+27)]= -1= -1= -28= -28= -22= -22加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变(a+b)+c=a+(b+c)一般地,任意若干个数相加,无论各
数相加的先后次序如何,其和都不变。a+b=b+a
例(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)计算例1、计算:(1) 15+(-13)+18(2) (-2.48)+4.33+(-7.52)+(-4.33)(3)15+18+(-13)=(15+18)+(-13)=33+(-13)=20解:(-2.48)+(-7.52)+4.33+(-4.33)=[(-2.48)+(-7.52)]+[4.33+(-4.33)]=(-10)+0=-10解:注意解题格式!解:使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。解题策略1、计算:
(1)5+(-7) +8
(2)
(3)(-3.5)+[3+(-1.5)]=5+8+(-7)=(5+8)+7=6=(-3.5)+(-1.5)+3 =[(-3.5)+(-1.5)]+3=-2用简便方法计算,并说明相关理由1)2)3)行家看“门道”例2、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15米,再向西行驶25米,然后又向东行驶20米,再向西行驶35米,问玩具赛车最后停在何处?一共行驶了多少米? -5-15-20-10051015-25西东A15-3520-25行家看“门道”例2、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15米,再向西行驶25米,然后又向东行驶20米,再向西行驶35米,问玩具赛车最后停在何处?一共行驶了多少米? 解:规定向东行驶为正,则
(+15)+(-25)+(+20)+(-35)=[(+15)+(+20)]+[(-25)+(-35)]=(+35)+(-60)=-25(米)
一共行驶的路程为|+15|+|-25|+|+20|+|-35|=95(米)
答:玩具赛车最后停在A地向西25米处,一共行驶了95米。 练习1:某升降机第一次上升8米,第二次又上升6米,第三次下降7米,第四次又下降了9米,这时升降机在初始位置的什么位置?升降机共运行了多少米?2. 蚂蚁从某点O出发在一条直线上来回爬行,假定向右爬行的路程为正数,向左爬行的路程为负数,爬过的各段路程依次为(单位:厘米)
+6,-3,+10,-5,-7,+13,-10
(1)蚂蚁最后是否回到了出发点?
(2)蚂蚁离开出发点O最远是多少厘米?
(3)在爬行过程中,如果爬行1厘米奖励一粒芝麻,则蚂蚁一共得到多少粒芝麻?小明记录了一星期每天的最低温度如下表:这个星期的平均最低温度是多少摄氏度?
平均最低温度=
最低温度之和
天数 数扩展到有理数后,下面这些结论还成立吗?请说明理由(如果认为结论不正确,请举例说明):
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数; ××(1)把正数和负数分别结合在一起相加(2)把互为相反数的结合,能凑整的结合(3)把同分母的数结合相加1.有理数加法交换律和结合律这一节课学习了什么内容?你学会了吗?2.运用加法交换律和结合律要注意:3.运算律的作用能使运算简便 用“﹥”或“﹤”符号填空
(1)如果a>0,b>0,那么a+b____0;
(2) 如果a<0,b<0,那么a+b____0;
(3) 如果a>0,b<0,|a|>|b|,那么a+b____0;
(4) 如果a<0,b>0,|a|<|b|,那么a+b____0;
探究如图,在钟面上有12个数字,如果在某些数前添上负号,可以使12个数字之和等于0,例如,-1+2+(-3)+4+(-5)+6+7+(-8)+9+
(-10)+11+(-12)=0;(1)请你再写出一种添加负号的方法;(2)想一想,这样的负号至少需添加几个?请举例说明.(3)以上解题过程中,你是怎样想的?开放题1、有下列说法:
(1)若干个有理数相加,和必大于任一个 加数。 (2)3个有理数相加,其和不可能为零。(3)若干个有理数相加的和仍然是有理数。 (4)两个有理数的和不大于两个有理数的绝对值的和。
其中正确的有几个?拓展练习:2、计算:
(-1)+2+(-3)+4+(-5)+6+(-7)+……+(-2011)+2012+(-2013)3、绝对值大于5,但不大于8的所有整数的和是多少?4、把6个圆圈排成如图所示的三角形,每边三个圆圈,把数字-7,-3,1,5,9,13分别填在这6个圆圈中,使各边上的数字之和相等。请填出符合条件的填法。5、若a+b+c=0,且b<c<0,
则下列结论正确的有几个:
(1)a+b>0;(2)b+c <0;
(3)c+a >0;(4)a-c <06、代数式 能取的最小值为多
少?此时x的值是多少?8、若a、b、c、d是互不相等的整数,且abcd=9,那么a+b+c+d等于多少?9、设三个互不相等的有理数,既可表示成1、a+b、a的形式,有可表示成0、a/b、b的形式,试求a2+b3的值。10、观察两个算式并回答问题:
算式:(1)63×67=6×(6+1)×100+3×7=4200+21=4221
(2)692×698=69×(69+1)×100+2×8=483000+16=483016
问题(1)两个因数各位上数字之和是多少?其余各位上的数字有什么特征?
(2)根据计算,猜想并举例验证符合上述特征的两数相乘的运算法则。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
