1.5 全等三角形的判定（2）课件

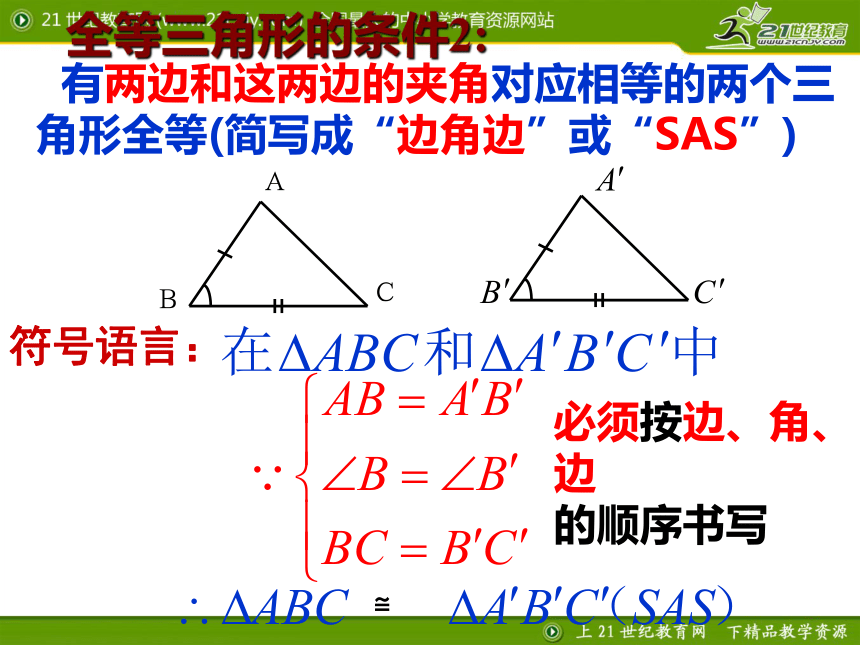
课件16张PPT。1.5三角形全等的判定（2）做一做：画△ABC,使AB=3cm，AC=4cm。画法：2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比较，它们互相重合吗？若再加一个条件，使∠A=45°，画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较，它们能互相重合吗？ 有两边和这两边的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)符号语言：全等三角形的条件2:≌必须按边、角、边
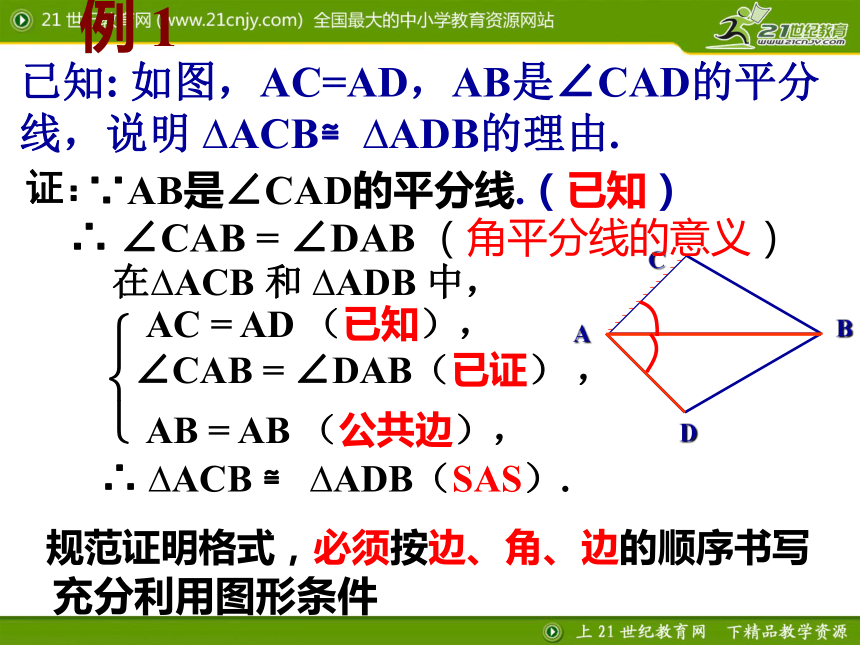
的顺序书写例 1已知: 如图，AC=AD，AB是∠CAD的平分线，说明 ?ACB≌?ADB的理由.ABCD在?ACB 和 ?ADB 中，AC = AD （已知），∠CAB = ∠DAB（已证） ，AB = AB （公共边），???∴ ?ACB ≌ ?ADB（SAS）.证：规范证明格式，必须按边、角、边的顺序书写∴ ∠CAB = ∠DAB （角平分线的意义）∵AB是∠CAD的平分线.（已知）充分利用图形条件1.如图，AC与BD相交于点O,
已知OA=OC, OB=OD,说明
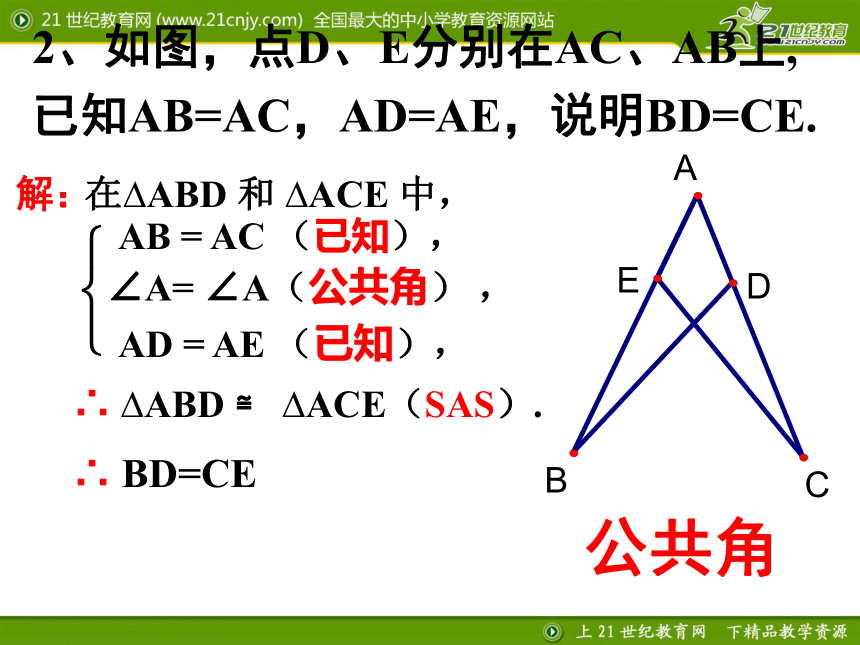
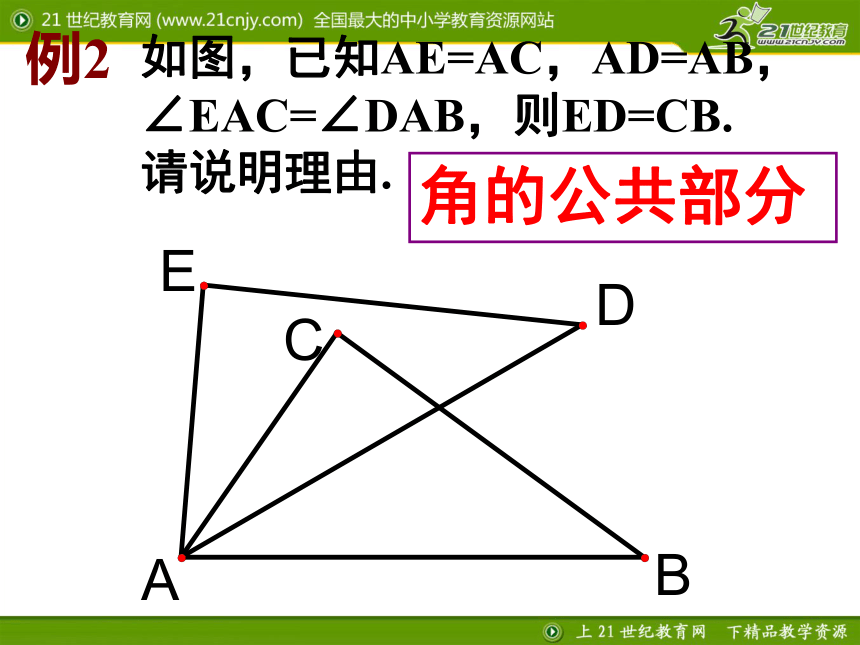
△AOB≌△COD的理由.练一练1证 ：在?AOB 和 ?COD 中，???OA=OC,OB=OD,∠AOB = ∠DOB，（已知）（已知）(已证）∴△AOB≌△COD. (SAS)(对顶角相等)∵AC与BD相交于点O∴∠AOB = ∠DOB .（已知），2、如图，点D、E分别在AC、AB上,已知AB=AC，AD=AE，说明BD=CE.在?ABD 和 ?ACE 中，AB = AC （已知），∠A= ∠A（公共角） ，AD = AE （已知），???∴ ?ABD ≌ ?ACE（SAS）.解：∴ BD=CE公共角如图，已知AE=AC，AD=AB，
∠EAC=∠DAB，则ED=CB.
请说明理由.例2角的公共部分 2、如图，已知DE⊥AC于E，BF⊥AC于F，DE=BF，AE=CF，求证：∠A=∠C .12解：∵DE⊥AC于E，BF⊥AC于F
∴ ∠1 =∠2=900∵AE=CF
∴AE+EF=CF+EF，即AF=CE在?CDE 和 ?ABF 中，DE = BF （已知），∠2=∠1（已证） ，CE = AF （已证），???∴ ?CDE ≌ ?ABF （SAS）.∴ ∠A =∠C（全等三角形对应角相等）.边的公共部分　　2.如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看．ABAC=DC?
∠ACB=∠DCE
BC=EC ∴AB=DE∴△ACB≌△DCE(SAS) 在△ACB≌△DCE中 中垂线上的点到线段两端点的距离相等证明命题：中垂线的定义：垂直于一条线段，并且平分这条线段的直线叫做这条线段的垂直平分线，简称中垂线.中垂线上的点到线段两端点的距离相等中垂线的性质：∵OC 是线段AB的中垂线
∴AC＝BC符号语言:中垂线的定义：垂直于一条线段，并且平分这条线段的直线叫做这条线段的垂直平分线，简称中垂线.想一想：1.如图，直线a和直线b分别是线段AB和线段AC的垂直平分线，
且相交于点O,请说出
点O到点A、B、C的
距离相等的理由.ab2. 如图， △ABC中，BC=10cm，AB的中垂线交于BC于D，AC的中垂线交BC于E,则△ADE的周长是______.ABCDE1.如图,在△ABＣ中,
AB=AC=10厘米，DE
是AB的中垂线，若△BDC的周长为16厘米,则BC的长为________．做一做你已经学会了几种三角形全等的判定方法？1、有三边对应相等的两个三角形全等.
简写成“边边边”或“SSS”2、两边和它们的夹角对应相等的两个三角形全等.简写成“边角边”或“SAS” .中垂线的定义中垂线上的点到线段两端点的距离相等中垂线的性质CABD4cm5cm45°4cm结论：两边及其一边所对的角对应相等，两个三角形不一定全等. 画△ABC，使BC=5cm，AB=4cm,
∠ACB=45°动手画一画