1.1--1.3三角形初步知识复习课件
文档属性
| 名称 | 1.1--1.3三角形初步知识复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 435.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-24 14:47:31 | ||
图片预览





文档简介
课件23张PPT。三角形的初步知识
1.1--1.3 复习课三角形的性质(1)边上的性质:三角形的两边之和大于第三边三角形的两边之差小于第三边(2)角上的性质:三角形三内角和等于180度三角形的一个外角等于和它不相邻的两个内角之和三角形的定义 由不在同一条直线上的三条线段首尾顺次
相接所组成的图形叫做三角形辨一辨:
1、下列每组分别是三根小木棒的长度,用它们能摆成三角形吗?(单位:厘米。填“能”或“不能”)
(1)3,4,5( )
(2)8,7,15( )
(3)13,12,20( )
(4)5,5,11( )不能不能能能直角三角形钝角三角形2、三角形按内角的大小分为三类:①锐角三角形;
②直角三角形;③钝角三角形。根据下列条件判断它们
是什么三角形?
(1)三个内角的度数是1:2:3( )
(2)两个内角是50°和30°( )c3、三角形的两边长分别是3和5,第三边a的取值范围( ) A、2≤a<8 B、2<a≤8
C、2<a<8 D、2≤a≤84、以下各组线段,能组成三角形的是( ) A.2cm,2cm,4cm B.3cm,6cm,8cm
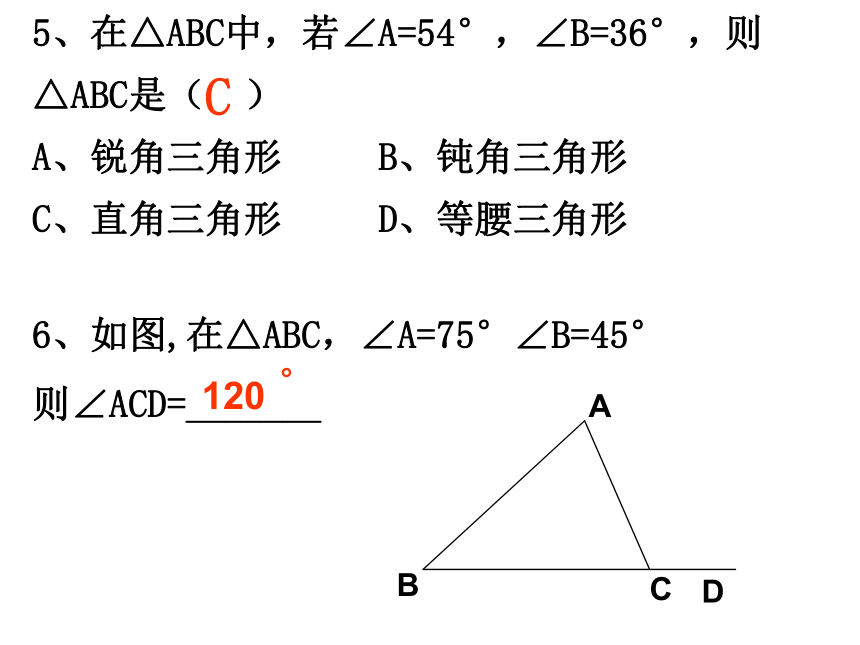
C.2cm,3cm,6cm D.4cm,6cm,11cmB5、在△ABC中,若∠A=54°,∠B=36°,则△ABC是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形C6、如图,在△ABC,∠A=75°∠B=45°
则∠ACD=_______
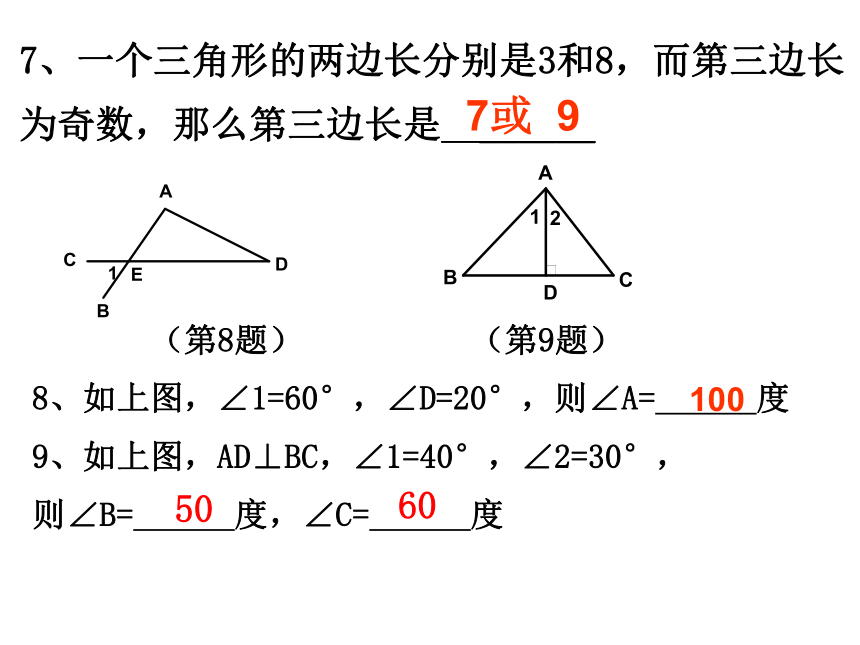
(第8题) (第9题)
8、如上图,∠1=60°,∠D=20°,则∠A= 度
9、如上图,AD⊥BC,∠1=40°,∠2=30°,
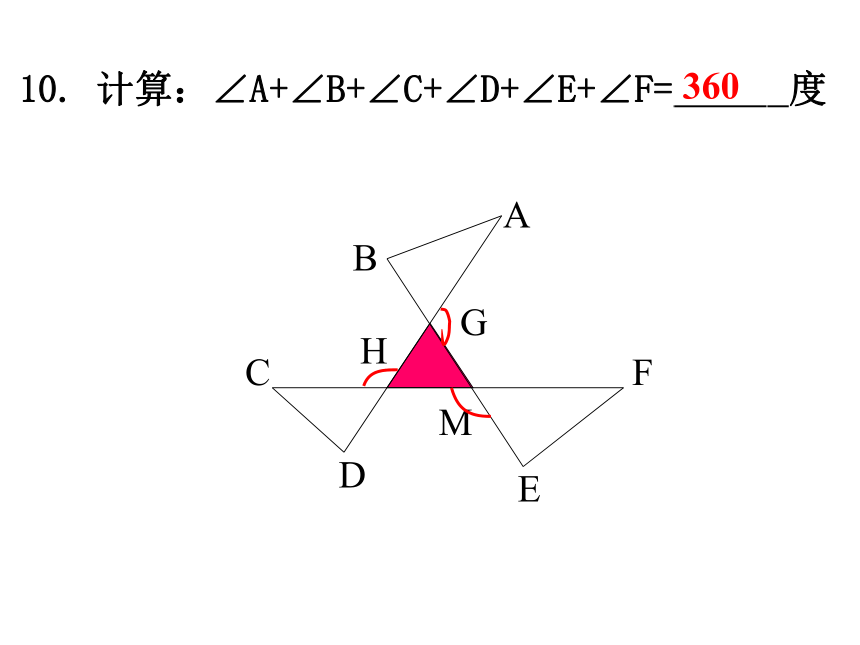
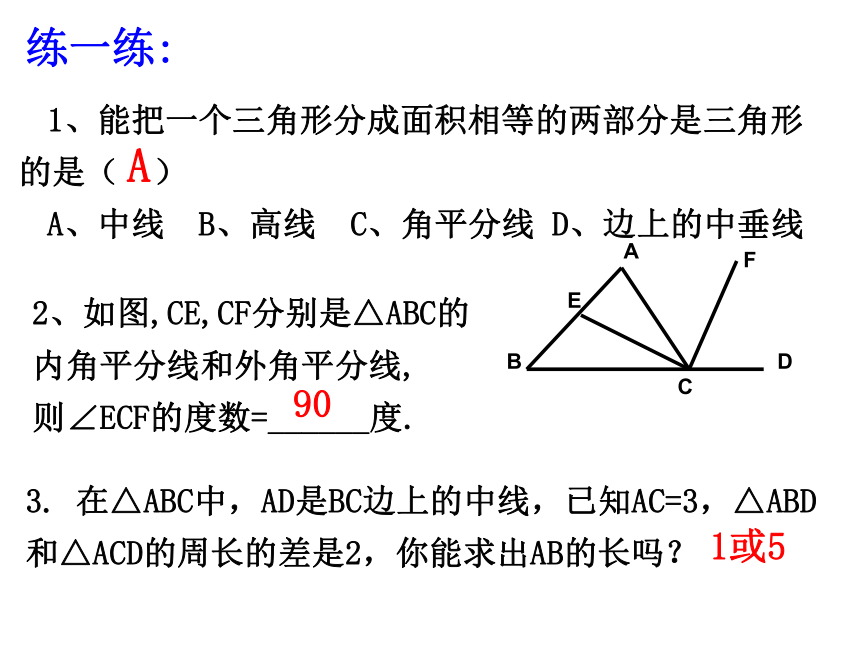
则∠B= 度,∠C= 度7或 910050607、一个三角形的两边长分别是3和8,而第三边长为奇数,那么第三边长是 ______ 10. 计算:∠A+∠B+∠C+∠D+∠E+∠F= 度BCDAGMHEF360 1、三角形的中线的概念2、三角形的角平分线的概念3、三角形的高的概念2、如图,CE,CF分别是△ABC的内角平分线和外角平分线,
则∠ECF的度数=______度.3. 在△ABC中,AD是BC边上的中线,已知AC=3,△ABD和△ACD的周长的差是2,你能求出AB的长吗?练一练:901或51、能把一个三角形分成面积相等的两部分是三角形 的是( )
A、中线 B、高线 C、角平分线 D、边上的中垂线A5、如图,在△ABC中,BD平分∠ABC,CE是AB边上的高,BD,CE交于点P。已知∠ABC=600,∠ACB=700, 求∠ACE,∠BDC的度数。400800ABCEDF4.如图,AD、BF都是△ABC的高线,若∠CAD=30度,则∠CBF=______度。30 8、如图,已知△ABC中,∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,则∠DAE= ; 1509、如图,BE、CF是△ABC 的角平分线,∠A=40°求∠BOC度数.1100把一副三角板按如图所示放置,已知∠A=45o,∠E=30o,
则两条斜边相交所成的钝角∠AOE的度数为 度改变条件:1、如图,BE、CF是△ABC 的外角平分线,
∠A=40°求∠BOC度数.7002、如图,BE、CF分别是△ABC 的内角与外角平分线,∠A=40°求∠BOC度数.200如图,在ΔABC中,∠C=90°,BE平分∠ABC,
AF平分外角∠BAD,BE与FA交与点E。求∠E的度数。
2.一般的,对某一件事情作出正确或不正确的判断的句子叫做命题.知识回顾4.从命题的条件出发,根据已知的定义、公理、定理,一步一步推得结论成立,这样的推理过程叫做证明.3.说明一个命题是假命题,只用找出一个反例,但要说明一个命题是真命题,就必须用推理的方法,而不能光凭一个例子.命题分为真命题与假命题.反例必须是具备命题的条件,却不具备命题的结论.1.能清楚地规定某一名称或术语的意
义的句子叫做该名称或术语的定义.证明命题的一般步骤:(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程.(1)理解题意:分清命题的条件(已知),结论(求证);(4)分析题意,探索证明思路;一、下列语句哪些是命题,哪些不是命题?
正数大于零,零大于一切负数;
两点确定一条直线;
画∠AOB的平分线;
是命题是命题不是命题练一练二、判断下列命题的真假.
1.有一个角是45°的直角三角形是等腰直角三角形.
2.素数不可能是偶数.
3.黄皮肤和黑皮肤的人都是中国人.
4.有两个外角(不同顶点)是钝角的三角形是锐角三角形.
5.若y(1-y)=0,则y=0.真命题假命题假命题假命题假命题练一练6.正数不小于它的倒数.
7.如果两个角不是对顶角,那么它们不相等.
8.若x<3,则x2<9.
9.异号两数相加和为负数.
10.若c>a+b,则c>a,c>b.假命题假命题假命题假命题假命题题设结论
三、判断下列语句是否为命题如
果是命题,把它改写成“如果……
那么……”形式.
证明命题“三角形不共顶点的三个外角的和等于360°”是真命题。已知:∠1 ,∠2, ∠3是△ ABC不共顶点的三个外角,求证: ∠1+∠2+∠3=360°证明:试一试1、(1) 如图(甲),在五角星图形中,求:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
(2) 把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?做一做B课堂小结 这节课你有何收获、困惑,
能与大家分享、交流你的感受吗?
1.1--1.3 复习课三角形的性质(1)边上的性质:三角形的两边之和大于第三边三角形的两边之差小于第三边(2)角上的性质:三角形三内角和等于180度三角形的一个外角等于和它不相邻的两个内角之和三角形的定义 由不在同一条直线上的三条线段首尾顺次
相接所组成的图形叫做三角形辨一辨:
1、下列每组分别是三根小木棒的长度,用它们能摆成三角形吗?(单位:厘米。填“能”或“不能”)
(1)3,4,5( )
(2)8,7,15( )
(3)13,12,20( )
(4)5,5,11( )不能不能能能直角三角形钝角三角形2、三角形按内角的大小分为三类:①锐角三角形;
②直角三角形;③钝角三角形。根据下列条件判断它们
是什么三角形?
(1)三个内角的度数是1:2:3( )
(2)两个内角是50°和30°( )c3、三角形的两边长分别是3和5,第三边a的取值范围( ) A、2≤a<8 B、2<a≤8
C、2<a<8 D、2≤a≤84、以下各组线段,能组成三角形的是( ) A.2cm,2cm,4cm B.3cm,6cm,8cm
C.2cm,3cm,6cm D.4cm,6cm,11cmB5、在△ABC中,若∠A=54°,∠B=36°,则△ABC是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形C6、如图,在△ABC,∠A=75°∠B=45°
则∠ACD=_______
(第8题) (第9题)
8、如上图,∠1=60°,∠D=20°,则∠A= 度
9、如上图,AD⊥BC,∠1=40°,∠2=30°,
则∠B= 度,∠C= 度7或 910050607、一个三角形的两边长分别是3和8,而第三边长为奇数,那么第三边长是 ______ 10. 计算:∠A+∠B+∠C+∠D+∠E+∠F= 度BCDAGMHEF360 1、三角形的中线的概念2、三角形的角平分线的概念3、三角形的高的概念2、如图,CE,CF分别是△ABC的内角平分线和外角平分线,
则∠ECF的度数=______度.3. 在△ABC中,AD是BC边上的中线,已知AC=3,△ABD和△ACD的周长的差是2,你能求出AB的长吗?练一练:901或51、能把一个三角形分成面积相等的两部分是三角形 的是( )
A、中线 B、高线 C、角平分线 D、边上的中垂线A5、如图,在△ABC中,BD平分∠ABC,CE是AB边上的高,BD,CE交于点P。已知∠ABC=600,∠ACB=700, 求∠ACE,∠BDC的度数。400800ABCEDF4.如图,AD、BF都是△ABC的高线,若∠CAD=30度,则∠CBF=______度。30 8、如图,已知△ABC中,∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,则∠DAE= ; 1509、如图,BE、CF是△ABC 的角平分线,∠A=40°求∠BOC度数.1100把一副三角板按如图所示放置,已知∠A=45o,∠E=30o,
则两条斜边相交所成的钝角∠AOE的度数为 度改变条件:1、如图,BE、CF是△ABC 的外角平分线,
∠A=40°求∠BOC度数.7002、如图,BE、CF分别是△ABC 的内角与外角平分线,∠A=40°求∠BOC度数.200如图,在ΔABC中,∠C=90°,BE平分∠ABC,
AF平分外角∠BAD,BE与FA交与点E。求∠E的度数。
2.一般的,对某一件事情作出正确或不正确的判断的句子叫做命题.知识回顾4.从命题的条件出发,根据已知的定义、公理、定理,一步一步推得结论成立,这样的推理过程叫做证明.3.说明一个命题是假命题,只用找出一个反例,但要说明一个命题是真命题,就必须用推理的方法,而不能光凭一个例子.命题分为真命题与假命题.反例必须是具备命题的条件,却不具备命题的结论.1.能清楚地规定某一名称或术语的意
义的句子叫做该名称或术语的定义.证明命题的一般步骤:(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程.(1)理解题意:分清命题的条件(已知),结论(求证);(4)分析题意,探索证明思路;一、下列语句哪些是命题,哪些不是命题?
正数大于零,零大于一切负数;
两点确定一条直线;
画∠AOB的平分线;
是命题是命题不是命题练一练二、判断下列命题的真假.
1.有一个角是45°的直角三角形是等腰直角三角形.
2.素数不可能是偶数.
3.黄皮肤和黑皮肤的人都是中国人.
4.有两个外角(不同顶点)是钝角的三角形是锐角三角形.
5.若y(1-y)=0,则y=0.真命题假命题假命题假命题假命题练一练6.正数不小于它的倒数.
7.如果两个角不是对顶角,那么它们不相等.
8.若x<3,则x2<9.
9.异号两数相加和为负数.
10.若c>a+b,则c>a,c>b.假命题假命题假命题假命题假命题题设结论
三、判断下列语句是否为命题如
果是命题,把它改写成“如果……
那么……”形式.
证明命题“三角形不共顶点的三个外角的和等于360°”是真命题。已知:∠1 ,∠2, ∠3是△ ABC不共顶点的三个外角,求证: ∠1+∠2+∠3=360°证明:试一试1、(1) 如图(甲),在五角星图形中,求:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
(2) 把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?做一做B课堂小结 这节课你有何收获、困惑,
能与大家分享、交流你的感受吗?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
