2022-2023学年浙教版九年级数学下册1.3 解直角三角形 同步练习 (word版 含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学下册1.3 解直角三角形 同步练习 (word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览



文档简介
浙教版九下 第1章 解直角三角形1.3 解直角三角形
一、选择题(共7小题)
1. 如图所示,某侦察机在空中 处发现敌方地面目标 ,此时从飞机上看目标 的俯角为 ,已知飞行高度 ,,则飞机到目标 的水平距离 为
A. B. C. D.
2. 如图所示,从热气球 处测得地面 , 两点的俯角分别是 ,,如果此时热气球 处的高度 为 ,点 ,, 在同一条直线上,那么 两点的距离是
A. B. C. D.
3. 如图所示,, 分别是一个湖的南、北两端 和 正东方向的两个村庄,,且 位于 的北偏东 方向上,则 的长为
A. B. C. D.
4. 如图所示,小鸟在港口 的北偏西 方向,距港口 海里的 处,货船从港口 出发,沿北偏东 方向匀速驶离港口 , 小时后货船在小鸟的正东方向,则货船的航行速度是
A. 海里/时 B. 海里/时 C. 海里/时 D. 海里/时
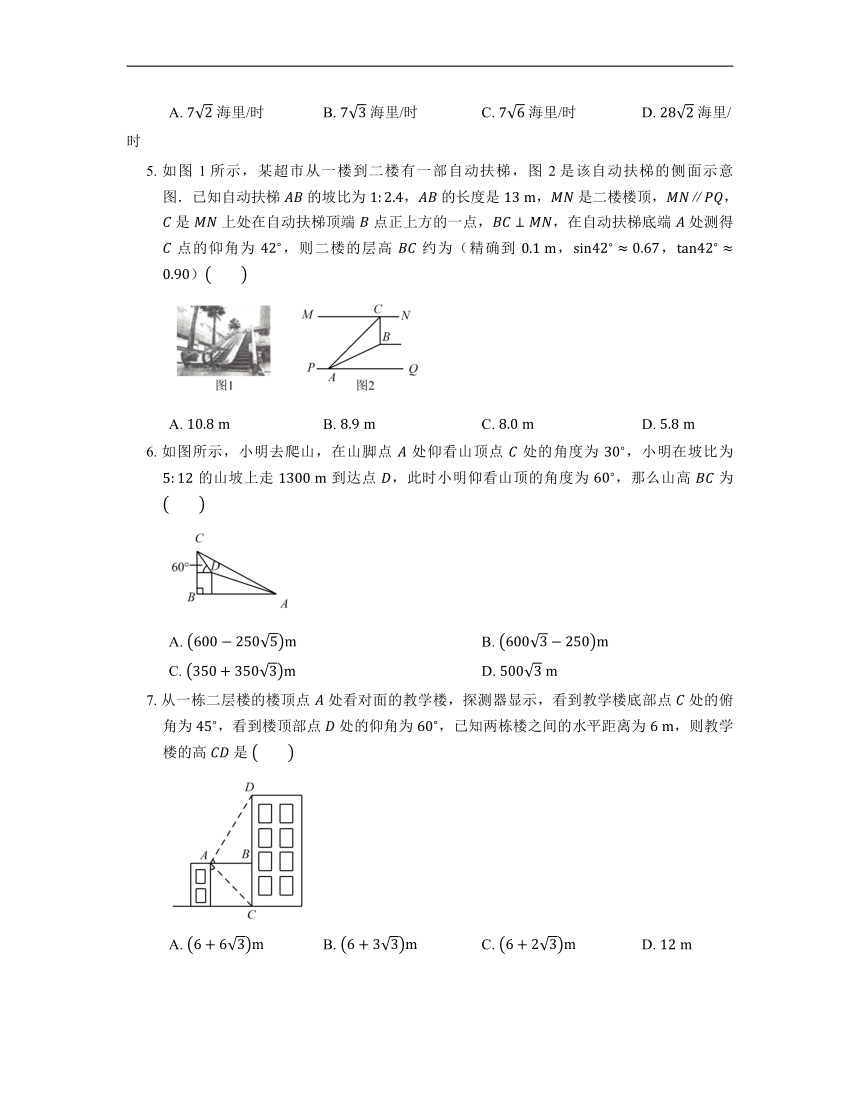
5. 如图 1所示,某超市从一楼到二楼有一部自动扶梯,图 2是该自动扶梯的侧面示意图.已知自动扶梯 的坡比为 , 的长度是 , 是二楼楼顶,, 是 上处在自动扶梯顶端 点正上方的一点,,在自动扶梯底端 处测得 点的仰角为 ,则二楼的层高 约为(精确到 ,,)
A. B. C. D.
6. 如图所示,小明去爬山,在山脚点 处仰看山顶点 处的角度为 ,小明在坡比为 的山坡上走 到达点 ,此时小明仰看山顶的角度为 ,那么山高 为
A. B.
C. D.
7. 从一栋二层楼的楼顶点 处看对面的教学楼,探测器显示,看到教学楼底部点 处的俯角为 ,看到楼顶部点 处的仰角为 ,已知两栋楼之间的水平距离为 ,则教学楼的高 是
A. B. C. D.
二、填空题(共5小题)
8. 为了缓解某市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆 高度是 ,从侧面 点测得显示牌顶端 点和底端 点的仰角分别是 和 ,则路况显示牌 的高度为 .
9. 如图所示,小明同学在距离某建筑物 的点 处测得条幅两端点 , 的仰角分别为 和 ,则条幅的高度 为 .
10. 如图所示,在小山的东侧 点有一个热气球,由于受西风的影晌,以 的速度沿与地面成 角的方向飞行, 后到达 处,此时热气球上的人测得小山西侧 点的俯角为 ,则小山东西两侧 , 两点间的距离为 .
11. 如图所示,一艘核潜艇在海面 下 的点 处测得俯角为 正前方的海底点 处有黑匣子,继续在同一深度直线航行 到达点 处测得正前方点 处的俯角为 .则海底点 处距离海面 的深度为 (结果精确到个位,参考数据;,,).
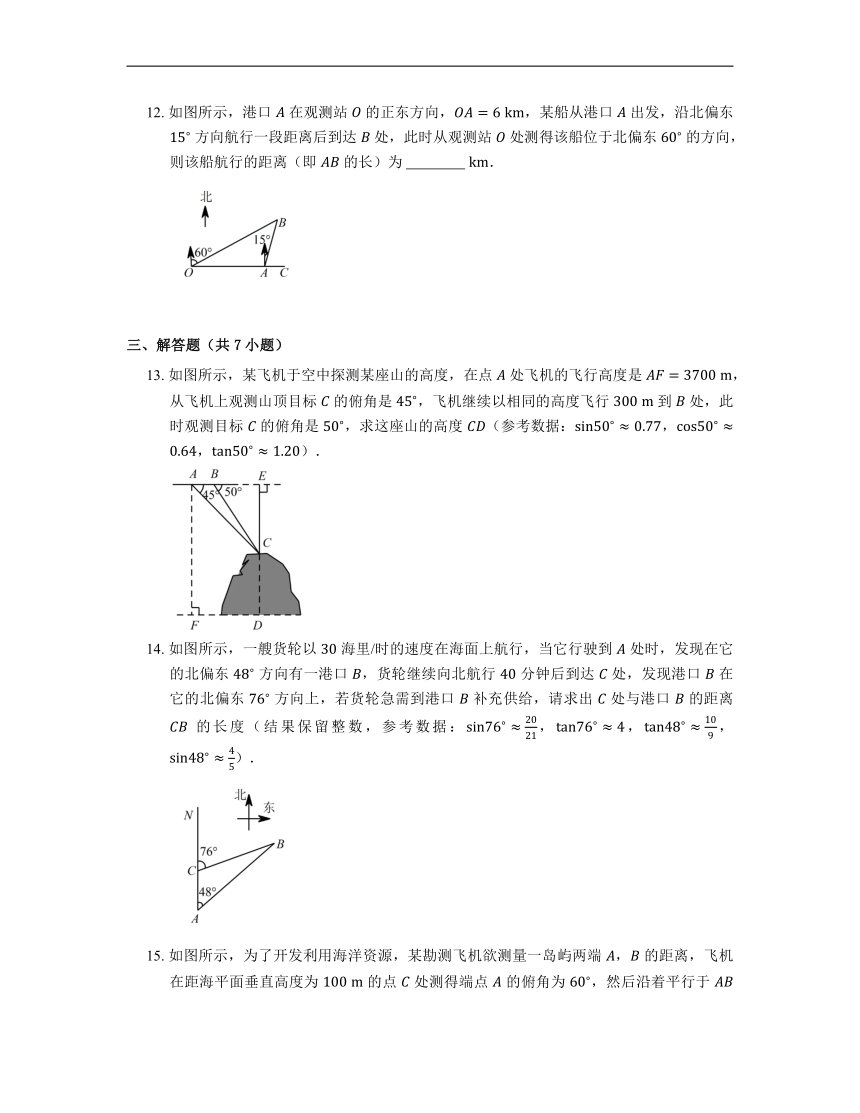
12. 如图所示,港口 在观测站 的正东方向,,某船从港口 出发,沿北偏东 方向航行一段距离后到达 处,此时从观测站 处测得该船位于北偏东 的方向,则该船航行的距离(即 的长)为 .
三、解答题(共7小题)
13. 如图所示,某飞机于空中探测某座山的高度,在点 处飞机的飞行高度是 ,从飞机上观测山顶目标 的俯角是 ,飞机继续以相同的高度飞行 到 处,此时观测目标 的俯角是 ,求这座山的高度 (参考数据:,,).
14. 如图所示,一艘货轮以 海里/时的速度在海面上航行,当它行驶到 处时,发现在它的北偏东 方向有一港口 ,货轮继续向北航行 分钟后到达 处,发现港口 在它的北偏东 方向上,若货轮急需到港口 补充供给,请求出 处与港口 的距离 的长度(结果保留整数,参考数据:,,,).
15. 如图所示,为了开发利用海洋资源,某勘测飞机欲测量一岛屿两端 , 的距离,飞机在距海平面垂直高度为 的点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 ,在点 测得端点 的俯角为 ,求岛屿两端 , 的距离(结果保留根号).
16. 如图所示,公路 为东西走向,在点 北偏东 方向上,距离 处是村庄 ;在点 北偏东 向上,距离 处是村庄 (参考数据:,,).
(1)求 , 两村之间的距离.
(2)要在公路 旁修建一个土特产收购站 ,使得 , 两村到 的距离之和最短,求这个最短距离.
17. 小明想知道湖中两个小亭 , 之间的距离,他在与小亭 , 位于同一水平面且东西走向的湖边小道 上某一观测点 处,测得亭 在点 的北偏东 ,亭 在点 的北偏东 ,当小明由点 沿小道 问东走 时,到达点 处,此时测得亭 恰好位于点 的正北方向,继续向东走 时到达点 处,此时亭 恰好位于点 的正北方向.根据以上测量数据,请你帮助小明计算湖中两个小亭 , 之间的距离.
18. 如图所示,泰州园博园中有一条人工河,河的两岸 , 互相平行,河岸 上有一排间隔为 的彩灯柱 ,,,,某人在河岸 的 处测得 ,然后沿河岸走了 到达 处,测得 ,求这条河的宽度(参考数据:,).
19. 如图所示,某剧组在东海拍摄广泛风光片,拍摄基地位于 处,在其正南方向 海里处有一小岛 ,在 的正东方向 海里处有一小岛 ,小岛 位于 上,且距小岛 海里.
(1)求 的度数(精确到 )和点 到 的距离;
(2)摄制组甲从 处乘甲船出发,沿 的方向匀速航行,摄制组乙从 处乘乙船出发,沿南偏西方向匀速直线航行,已知甲船的速度是乙船的 倍,若两船同时出发并且在 , 间的 处相遇,问相遇时乙船航行了多少海里(结果精确到 海里)
答案
1. A
2. D
3. B
4. A
5. D
6. B
7. A
8.
9.
10.
11.
12.
13. 设 ,在 中,,则 ,在 中,,则 .
,
,
解得 .
这座山的高度
14. 如图所示,过点 作 于点 ,
(海里),
在 中,,
则 ,
在 中,,
即 ,
于是 ,
解得 (海里),(海里),
在 中,,,
则 海里.
15. 如图所示,过点 作 于点 ,过点 作 于点 .
,
.
四边形 为矩形.
,.
由题意可知 ,.
在 中,,.
.
在 中,,.
.
.
岛屿两端 , 的距离为 .
16. (1) 如图所示,过点 作 ,过点 作 于点 .
在 中,
,,
因为 ,
所以 ,.
在 中,
,,
因为 ,
所以 ,.
所以 ..
在 中,
.
(2) 作点 关于 的对称点 ,连接 交 于点 ,点 即为站点,
此时 ,
在 中,
.
所以最短距离为 .
17. 如图所示,连接 ,.
点 在点 的正北方向,点 在点 的正北方向,
,.
在 中,,
.
在 中,,
.
.
如图所示,过点 作 于点 ,
则 .
在 中,,
,
.
湖中两个小亭 , 之间的距离为 .
18. 如图所示,作 ,,垂足分别为 ,.
由题意知,四边形 为矩形,
,.
设这条河的宽度为 .
在 中,
,
.
在 中,
.
,
,
解得 ,
即这条河的宽度为 .
19. (1) 如图所示,过点 作 于点 .
在 中,
,
.
,
而 ,
.
(海里).
到 的距离为 海里.
(2) 设相遇时乙船航行了 海里,则 ,.
,,
.
.
在 中,
,
解得 (不合题意,舍去),.
相遇时乙船航行了 海里.
一、选择题(共7小题)
1. 如图所示,某侦察机在空中 处发现敌方地面目标 ,此时从飞机上看目标 的俯角为 ,已知飞行高度 ,,则飞机到目标 的水平距离 为
A. B. C. D.
2. 如图所示,从热气球 处测得地面 , 两点的俯角分别是 ,,如果此时热气球 处的高度 为 ,点 ,, 在同一条直线上,那么 两点的距离是
A. B. C. D.
3. 如图所示,, 分别是一个湖的南、北两端 和 正东方向的两个村庄,,且 位于 的北偏东 方向上,则 的长为
A. B. C. D.
4. 如图所示,小鸟在港口 的北偏西 方向,距港口 海里的 处,货船从港口 出发,沿北偏东 方向匀速驶离港口 , 小时后货船在小鸟的正东方向,则货船的航行速度是
A. 海里/时 B. 海里/时 C. 海里/时 D. 海里/时
5. 如图 1所示,某超市从一楼到二楼有一部自动扶梯,图 2是该自动扶梯的侧面示意图.已知自动扶梯 的坡比为 , 的长度是 , 是二楼楼顶,, 是 上处在自动扶梯顶端 点正上方的一点,,在自动扶梯底端 处测得 点的仰角为 ,则二楼的层高 约为(精确到 ,,)
A. B. C. D.
6. 如图所示,小明去爬山,在山脚点 处仰看山顶点 处的角度为 ,小明在坡比为 的山坡上走 到达点 ,此时小明仰看山顶的角度为 ,那么山高 为
A. B.
C. D.
7. 从一栋二层楼的楼顶点 处看对面的教学楼,探测器显示,看到教学楼底部点 处的俯角为 ,看到楼顶部点 处的仰角为 ,已知两栋楼之间的水平距离为 ,则教学楼的高 是
A. B. C. D.
二、填空题(共5小题)
8. 为了缓解某市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆 高度是 ,从侧面 点测得显示牌顶端 点和底端 点的仰角分别是 和 ,则路况显示牌 的高度为 .
9. 如图所示,小明同学在距离某建筑物 的点 处测得条幅两端点 , 的仰角分别为 和 ,则条幅的高度 为 .
10. 如图所示,在小山的东侧 点有一个热气球,由于受西风的影晌,以 的速度沿与地面成 角的方向飞行, 后到达 处,此时热气球上的人测得小山西侧 点的俯角为 ,则小山东西两侧 , 两点间的距离为 .
11. 如图所示,一艘核潜艇在海面 下 的点 处测得俯角为 正前方的海底点 处有黑匣子,继续在同一深度直线航行 到达点 处测得正前方点 处的俯角为 .则海底点 处距离海面 的深度为 (结果精确到个位,参考数据;,,).
12. 如图所示,港口 在观测站 的正东方向,,某船从港口 出发,沿北偏东 方向航行一段距离后到达 处,此时从观测站 处测得该船位于北偏东 的方向,则该船航行的距离(即 的长)为 .
三、解答题(共7小题)
13. 如图所示,某飞机于空中探测某座山的高度,在点 处飞机的飞行高度是 ,从飞机上观测山顶目标 的俯角是 ,飞机继续以相同的高度飞行 到 处,此时观测目标 的俯角是 ,求这座山的高度 (参考数据:,,).
14. 如图所示,一艘货轮以 海里/时的速度在海面上航行,当它行驶到 处时,发现在它的北偏东 方向有一港口 ,货轮继续向北航行 分钟后到达 处,发现港口 在它的北偏东 方向上,若货轮急需到港口 补充供给,请求出 处与港口 的距离 的长度(结果保留整数,参考数据:,,,).
15. 如图所示,为了开发利用海洋资源,某勘测飞机欲测量一岛屿两端 , 的距离,飞机在距海平面垂直高度为 的点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 ,在点 测得端点 的俯角为 ,求岛屿两端 , 的距离(结果保留根号).
16. 如图所示,公路 为东西走向,在点 北偏东 方向上,距离 处是村庄 ;在点 北偏东 向上,距离 处是村庄 (参考数据:,,).
(1)求 , 两村之间的距离.
(2)要在公路 旁修建一个土特产收购站 ,使得 , 两村到 的距离之和最短,求这个最短距离.
17. 小明想知道湖中两个小亭 , 之间的距离,他在与小亭 , 位于同一水平面且东西走向的湖边小道 上某一观测点 处,测得亭 在点 的北偏东 ,亭 在点 的北偏东 ,当小明由点 沿小道 问东走 时,到达点 处,此时测得亭 恰好位于点 的正北方向,继续向东走 时到达点 处,此时亭 恰好位于点 的正北方向.根据以上测量数据,请你帮助小明计算湖中两个小亭 , 之间的距离.
18. 如图所示,泰州园博园中有一条人工河,河的两岸 , 互相平行,河岸 上有一排间隔为 的彩灯柱 ,,,,某人在河岸 的 处测得 ,然后沿河岸走了 到达 处,测得 ,求这条河的宽度(参考数据:,).
19. 如图所示,某剧组在东海拍摄广泛风光片,拍摄基地位于 处,在其正南方向 海里处有一小岛 ,在 的正东方向 海里处有一小岛 ,小岛 位于 上,且距小岛 海里.
(1)求 的度数(精确到 )和点 到 的距离;
(2)摄制组甲从 处乘甲船出发,沿 的方向匀速航行,摄制组乙从 处乘乙船出发,沿南偏西方向匀速直线航行,已知甲船的速度是乙船的 倍,若两船同时出发并且在 , 间的 处相遇,问相遇时乙船航行了多少海里(结果精确到 海里)
答案
1. A
2. D
3. B
4. A
5. D
6. B
7. A
8.
9.
10.
11.
12.
13. 设 ,在 中,,则 ,在 中,,则 .
,
,
解得 .
这座山的高度
14. 如图所示,过点 作 于点 ,
(海里),
在 中,,
则 ,
在 中,,
即 ,
于是 ,
解得 (海里),(海里),
在 中,,,
则 海里.
15. 如图所示,过点 作 于点 ,过点 作 于点 .
,
.
四边形 为矩形.
,.
由题意可知 ,.
在 中,,.
.
在 中,,.
.
.
岛屿两端 , 的距离为 .
16. (1) 如图所示,过点 作 ,过点 作 于点 .
在 中,
,,
因为 ,
所以 ,.
在 中,
,,
因为 ,
所以 ,.
所以 ..
在 中,
.
(2) 作点 关于 的对称点 ,连接 交 于点 ,点 即为站点,
此时 ,
在 中,
.
所以最短距离为 .
17. 如图所示,连接 ,.
点 在点 的正北方向,点 在点 的正北方向,
,.
在 中,,
.
在 中,,
.
.
如图所示,过点 作 于点 ,
则 .
在 中,,
,
.
湖中两个小亭 , 之间的距离为 .
18. 如图所示,作 ,,垂足分别为 ,.
由题意知,四边形 为矩形,
,.
设这条河的宽度为 .
在 中,
,
.
在 中,
.
,
,
解得 ,
即这条河的宽度为 .
19. (1) 如图所示,过点 作 于点 .
在 中,
,
.
,
而 ,
.
(海里).
到 的距离为 海里.
(2) 设相遇时乙船航行了 海里,则 ,.
,,
.
.
在 中,
,
解得 (不合题意,舍去),.
相遇时乙船航行了 海里.
