1.3.3数制 课件 2022-2023学年浙教版(2019)高中信息技术必修1(20张PPT)
文档属性
| 名称 | 1.3.3数制 课件 2022-2023学年浙教版(2019)高中信息技术必修1(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-08-28 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
1.3 数据采集与编码
1.数制及定义
2.二进制、十进制、十六进制
3.N进制转十进制
4.十进制转N进制
5.二进制与十六进制
学习目标:
1
数制
一、数制概念
进位计数法
是人为定义的带进位的计数方式
N进制: 对于任何一种进制N进制,表示某一位置上的数运算时是逢N进一位
用有限种数字符号表示所有的数值
位值计数法
数制包含两个基本要素:基和权
基:基数,是组成数制的数码个数
权:权值,指每一个数位上的1对应的数值,可以表示为基数的若干次幂。
二、常用进制
在计算机内部,数据以二进制形式存在
三、N进制转换为十进制
5
4
3
2
1
0
6
(
)n
n0
n1
n6
即 1011B=11D
任何进制转换为十进制,都可以用位权相加法
(1675)8=( )10
(1111)2=( )10
(FF)16=( )10
即 3CH=60D
957
15
255
十进制转换为N进制(整数部分),可用除N取余,逆向排列。
273=( )8
15=( )2
35=( )16
13D=1101B
60D=3CH
四、十进制转换为N进制
421
23
1111
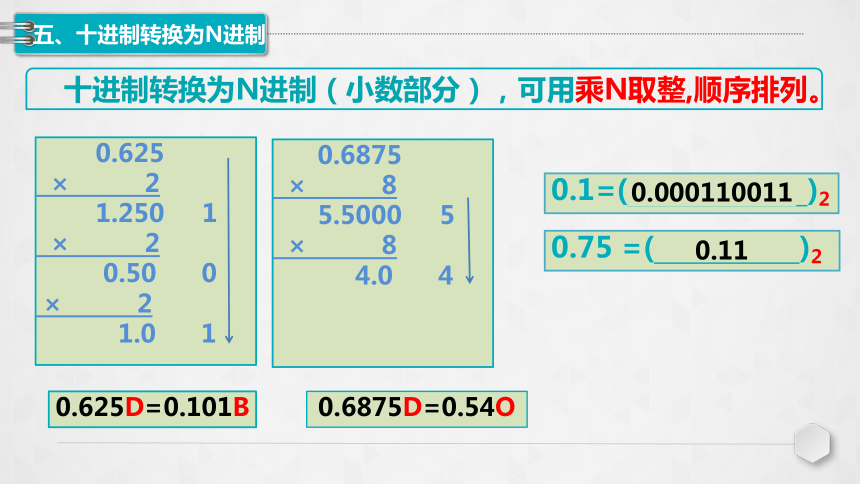
十进制转换为N进制(小数部分),可用乘N取整,顺序排列。
0.1=( )2
0.75 =( )2
0.625D=0.101B
0.6875D=0.54O
五、十进制转换为N进制
0.000110011
0.11
0.625
× 2
1.250 1
× 2
0.50 0
× 2
1.0 1
0.6875
× 8
5.5000 5
× 8
4.0 4
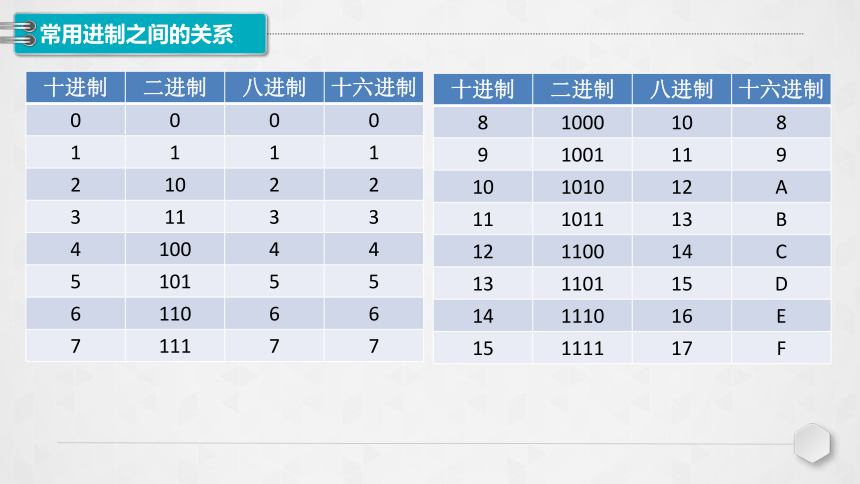
常用进制之间的关系
十进制 二进制 八进制 十六进制
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
十进制 二进制 八进制 十六进制
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
二进制与十六进制互转:四位对一位,一位对四位
五、二进制与十六进制
所以:111010B= 3A H
0011
111010B= H
0011 1010
111010
1010
3AH= B
所以:3AH= 111010 B
A
3
进制转换小结
十进制
二进制
十六进制
除2倒取余
除16倒取余
位权相加
位权相加
4位转1位
1位转4位
1、 计算机中的数据是用( )表示的
A.字母 B. ASCII码
C.二进制数字代码 D.英文
课堂练习
C
2、 下列数值最小的是( )
A. 1101B B. 1AH
C. 12D D. 16D
C
3、 二进制的 1101 转化成十进制等于( )。
A. 20 B. 18
C. 13 D. 16
课堂练习
C
解析:1101(2)=1*20+0*21+1*22+1*23=1+0+4+8=13
4、 26(16)转化为十进制为( )
A. 28 B. 38
C. 43 D. 36
课堂练习
B
解析:26(16)=6*160+2*161=38
5、 106转化为二进制为( )
A. 1101010 B. 1001101
C. 1101101 D. 1001010
课堂练习
A
6、十六进制数4B用二进制数来表示,下列选项中正确的是( )
A.1001001 B. 1001011
C. 1010101 D. 1011011
B
7、二进制数11101转换成十进制数是 ( )
A.29 B.68 C.17 D.35
8、 十进制数71转换成二进制数是( )
A.1000111 B. 1110001 C.1001100 D.1000011
9、 二进制数1111010换成十六进制数是( )
A.6B B.7B C.7A D.710
A
A
C
计算器转换小技巧
课堂小结
转换 方法
十进制转N进制 (整数)除N取余,逆向排列;
(小数)乘N取整,顺向排列
N进制转十进制 按权展开,相加求和
二进制转十六进制 四位变一位,不足位补0
十六进制转二进制 一位变四位,不足位补0
二进制转八进制 三位变一位,不足位补0
八进制转二进制 一位变三位,不足位补0
思 考
将1000个苹果放入10个箱子。要取走1~1000中任意个数的苹果,要求不拆开箱子,应如何装箱?
谢谢!
1.3 数据采集与编码
1.数制及定义
2.二进制、十进制、十六进制
3.N进制转十进制
4.十进制转N进制
5.二进制与十六进制
学习目标:
1
数制
一、数制概念
进位计数法
是人为定义的带进位的计数方式
N进制: 对于任何一种进制N进制,表示某一位置上的数运算时是逢N进一位
用有限种数字符号表示所有的数值
位值计数法
数制包含两个基本要素:基和权
基:基数,是组成数制的数码个数
权:权值,指每一个数位上的1对应的数值,可以表示为基数的若干次幂。
二、常用进制
在计算机内部,数据以二进制形式存在
三、N进制转换为十进制
5
4
3
2
1
0
6
(
)n
n0
n1
n6
即 1011B=11D
任何进制转换为十进制,都可以用位权相加法
(1675)8=( )10
(1111)2=( )10
(FF)16=( )10
即 3CH=60D
957
15
255
十进制转换为N进制(整数部分),可用除N取余,逆向排列。
273=( )8
15=( )2
35=( )16
13D=1101B
60D=3CH
四、十进制转换为N进制
421
23
1111
十进制转换为N进制(小数部分),可用乘N取整,顺序排列。
0.1=( )2
0.75 =( )2
0.625D=0.101B
0.6875D=0.54O
五、十进制转换为N进制
0.000110011
0.11
0.625
× 2
1.250 1
× 2
0.50 0
× 2
1.0 1
0.6875
× 8
5.5000 5
× 8
4.0 4
常用进制之间的关系
十进制 二进制 八进制 十六进制
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
十进制 二进制 八进制 十六进制
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
二进制与十六进制互转:四位对一位,一位对四位
五、二进制与十六进制
所以:111010B= 3A H
0011
111010B= H
0011 1010
111010
1010
3AH= B
所以:3AH= 111010 B
A
3
进制转换小结
十进制
二进制
十六进制
除2倒取余
除16倒取余
位权相加
位权相加
4位转1位
1位转4位
1、 计算机中的数据是用( )表示的
A.字母 B. ASCII码
C.二进制数字代码 D.英文
课堂练习
C
2、 下列数值最小的是( )
A. 1101B B. 1AH
C. 12D D. 16D
C
3、 二进制的 1101 转化成十进制等于( )。
A. 20 B. 18
C. 13 D. 16
课堂练习
C
解析:1101(2)=1*20+0*21+1*22+1*23=1+0+4+8=13
4、 26(16)转化为十进制为( )
A. 28 B. 38
C. 43 D. 36
课堂练习
B
解析:26(16)=6*160+2*161=38
5、 106转化为二进制为( )
A. 1101010 B. 1001101
C. 1101101 D. 1001010
课堂练习
A
6、十六进制数4B用二进制数来表示,下列选项中正确的是( )
A.1001001 B. 1001011
C. 1010101 D. 1011011
B
7、二进制数11101转换成十进制数是 ( )
A.29 B.68 C.17 D.35
8、 十进制数71转换成二进制数是( )
A.1000111 B. 1110001 C.1001100 D.1000011
9、 二进制数1111010换成十六进制数是( )
A.6B B.7B C.7A D.710
A
A
C
计算器转换小技巧
课堂小结
转换 方法
十进制转N进制 (整数)除N取余,逆向排列;
(小数)乘N取整,顺向排列
N进制转十进制 按权展开,相加求和
二进制转十六进制 四位变一位,不足位补0
十六进制转二进制 一位变四位,不足位补0
二进制转八进制 三位变一位,不足位补0
八进制转二进制 一位变三位,不足位补0
思 考
将1000个苹果放入10个箱子。要取走1~1000中任意个数的苹果,要求不拆开箱子,应如何装箱?
谢谢!
