浙教版八年级下册 5.2.1 菱形 课件(共19张PPT)
文档属性
| 名称 | 浙教版八年级下册 5.2.1 菱形 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 19:35:36 | ||
图片预览



文档简介
(共18张PPT)
浙教版八年级下册第五单元第二节第一课时
活动探究,形成概念
画一画:
你能画出周长为8cm且边长为整数的平行四边形吗?
问:与图①图②相比,图③与图④有什么共同特点?
四条边都相等
①
②
③
④
请先按暂停键!思考完成后
再按回播放键!
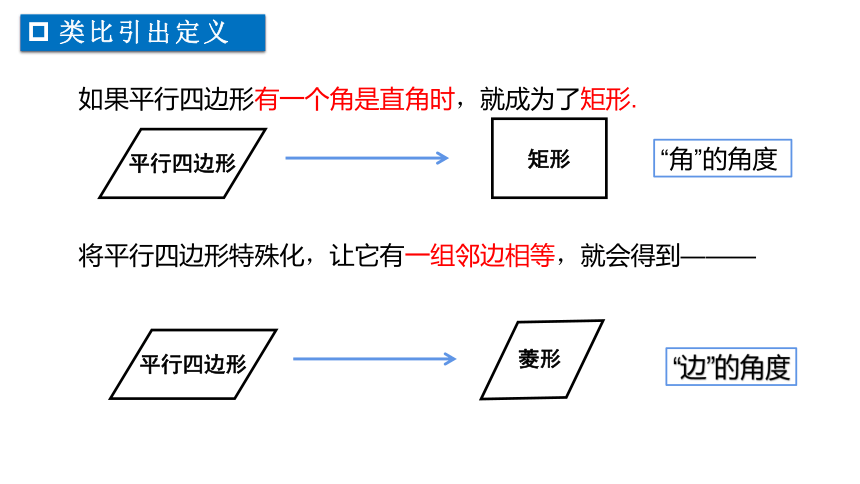
类比引出定义
平行四边形
矩形
如果平行四边形有一个角是直角时,就成为了矩形.
将平行四边形特殊化,让它有一组邻边相等,就会得到———
菱形
平行四边形
“角”的角度
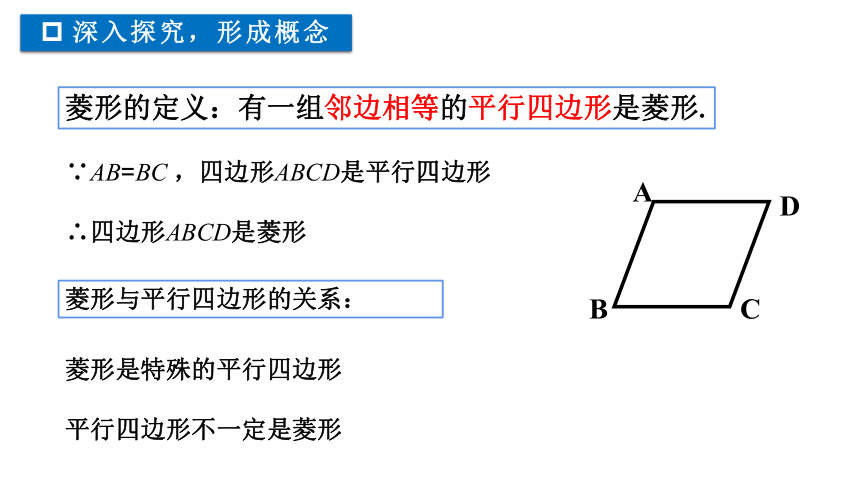
深入探究,形成概念
菱形的定义:有一组邻边相等的平行四边形是菱形.
菱形是特殊的平行四边形
平行四边形不一定是菱形
A
B
D
C
∵AB=BC ,四边形ABCD是平行四边形
∴四边形ABCD是菱形
菱形与平行四边形的关系:
深入探究,形成概念
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
思考:菱形有哪些特殊性质呢?
感受生活,菱形就在我们身边
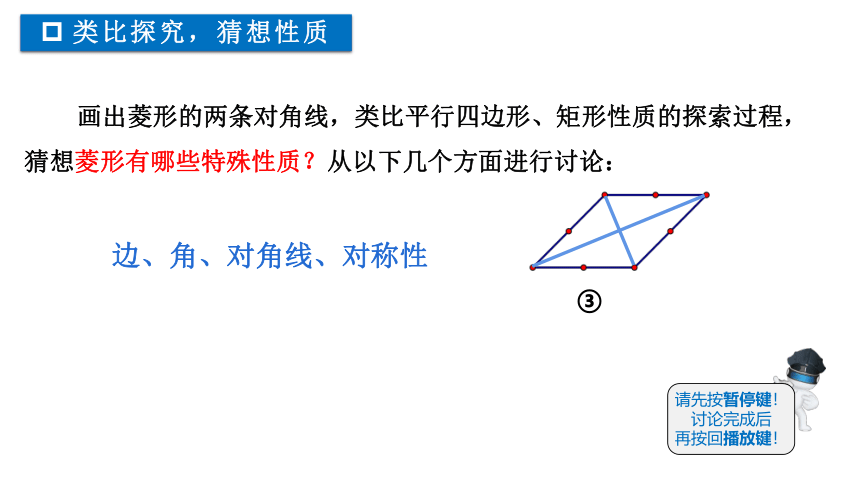
类比探究,猜想性质
画出菱形的两条对角线,类比平行四边形、矩形性质的探索过程,猜想菱形有哪些特殊性质?从以下几个方面进行讨论:
边、角、对角线、对称性
③
请先按暂停键!讨论完成后
再按回播放键!
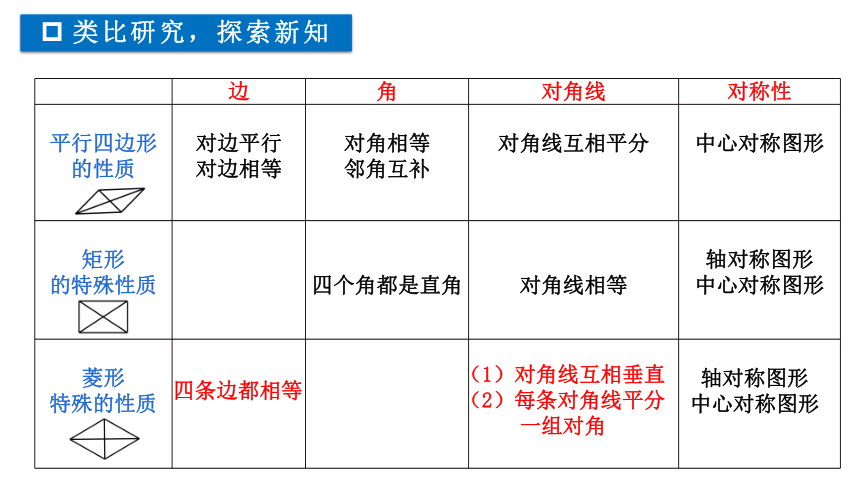
类比研究,探索新知
边 角 对角线 对称性
平行四边形的性质
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
中心对称图形
矩形
的特殊性质
四个角都是直角
对角线相等
轴对称图形
中心对称图形
菱形
特殊的性质
四条边都相等
(1)对角线互相垂直
(2)每条对角线平分一组对角
轴对称图形
中心对称图形
梳理新知,及时巩固
性质定理2:(1)菱形的对角线互相垂直
(2)每条对角线平分一组对角
性质定理1:菱形的四条边都相等
(边)
(对角线)
∵四边形ABCD是菱形
∵DO=DO
∴△AOD≌△COD(SSS)
∴∠AOD=∠COD=90°
∴AC⊥BD
证明:
同理,BD平分∠ABC,AC平分∠BAD和∠BCD
请先按暂停键!书写证明过程,写完后
再按回播放键!
∴AD=CD,AO=CO
∴∠ADO=∠CDO
∴BD平分∠ADC
演绎推理,掌握新知
O
D
B
C
A
已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.
求证: (1)AC⊥BD;
(2)AC平分∠BAD和∠BCD,BD平分∠ADC 和∠ABC.
演绎推理,掌握新知
∵四边形ABCD是菱形,
∴AB=AD
(菱形的定义),
BO=DO
(平行四边形的对角线互相平分),
∴AC⊥BD,AC平分∠BAD
同理,AC平分∠BCD,BD平分∠ABC和∠ADC
(等腰三角形三线合一)
O
D
B
C
A
法二:
菱 形
三角形
转化
辨析定义,强化性质
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
2.菱形具有而矩形不一定有的性质是( )
A.对角线互相平分 B.四条边相等
C.对角相等 D.邻角互补
D
B
在菱形ABCD中,边长是 10,
40
16
渐进变式,内化性质
例:
(1)求菱形的周长.
(2)若BD=12,求AC的长.
请先按暂停键!思考完成后
再按回播放键!
AC=16
在菱形ABCD中,
渐进变式,内化性质
例:
若BD=12,AC=16,求菱形的面积.
请先按暂停键!思考完成后
再按回播放键!
∴AC⊥BD
OB= OD= BD=6
解:∵四边形ABCD是菱形
∴S菱形ABCD=S△ACD+S△ABC
在菱形ABCD中,
渐进变式,内化性质
例:
请先按暂停键!思考完成后
再按回播放键!
a
b
S菱形ABCD=S△ACD+S△ABC
菱形的面积=底×高=对角线乘积的一半.
若BD= ,AC= ,求菱形的面积.
变式:
解:
在菱形ABCD中,边长是 10,
40
16
渐进变式,内化性质
例:
(1)求菱形的周长.
(2)若BD=12,求AC的长.
(3)若∠BAC = 30°,求AC的长.
请先按暂停键!思考完成后
再按回播放键!
解:∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
AC⊥BD(菱形的对角线互相垂直)
∵∠BAC=30°
∴∠BAD=60°
∴△ABD是等边三角形.
∴OB=OD=5
又由勾股定理,得AO=
AC=2AO=
渐进变式,内化性质
(3)若∠BAC= 30°,求AC的长.
在菱形ABCD中,边长是 10,
例:
纵观过去,指引未来
四边形
平行四边形
边特殊化
我们学行四边形、矩形,通过类比,学习菱形
定义
性质
定义
性质
边
角
对角线
对称性
判定
应用
角特殊化
菱形
矩形
定义
性质
边
角
对角线
对称性
判定
应用
边特殊化
同学们再见
浙教版八年级下册第五单元第二节第一课时
活动探究,形成概念
画一画:
你能画出周长为8cm且边长为整数的平行四边形吗?
问:与图①图②相比,图③与图④有什么共同特点?
四条边都相等
①
②
③
④
请先按暂停键!思考完成后
再按回播放键!
类比引出定义
平行四边形
矩形
如果平行四边形有一个角是直角时,就成为了矩形.
将平行四边形特殊化,让它有一组邻边相等,就会得到———
菱形
平行四边形
“角”的角度
深入探究,形成概念
菱形的定义:有一组邻边相等的平行四边形是菱形.
菱形是特殊的平行四边形
平行四边形不一定是菱形
A
B
D
C
∵AB=BC ,四边形ABCD是平行四边形
∴四边形ABCD是菱形
菱形与平行四边形的关系:
深入探究,形成概念
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
思考:菱形有哪些特殊性质呢?
感受生活,菱形就在我们身边
类比探究,猜想性质
画出菱形的两条对角线,类比平行四边形、矩形性质的探索过程,猜想菱形有哪些特殊性质?从以下几个方面进行讨论:
边、角、对角线、对称性
③
请先按暂停键!讨论完成后
再按回播放键!
类比研究,探索新知
边 角 对角线 对称性
平行四边形的性质
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
中心对称图形
矩形
的特殊性质
四个角都是直角
对角线相等
轴对称图形
中心对称图形
菱形
特殊的性质
四条边都相等
(1)对角线互相垂直
(2)每条对角线平分一组对角
轴对称图形
中心对称图形
梳理新知,及时巩固
性质定理2:(1)菱形的对角线互相垂直
(2)每条对角线平分一组对角
性质定理1:菱形的四条边都相等
(边)
(对角线)
∵四边形ABCD是菱形
∵DO=DO
∴△AOD≌△COD(SSS)
∴∠AOD=∠COD=90°
∴AC⊥BD
证明:
同理,BD平分∠ABC,AC平分∠BAD和∠BCD
请先按暂停键!书写证明过程,写完后
再按回播放键!
∴AD=CD,AO=CO
∴∠ADO=∠CDO
∴BD平分∠ADC
演绎推理,掌握新知
O
D
B
C
A
已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.
求证: (1)AC⊥BD;
(2)AC平分∠BAD和∠BCD,BD平分∠ADC 和∠ABC.
演绎推理,掌握新知
∵四边形ABCD是菱形,
∴AB=AD
(菱形的定义),
BO=DO
(平行四边形的对角线互相平分),
∴AC⊥BD,AC平分∠BAD
同理,AC平分∠BCD,BD平分∠ABC和∠ADC
(等腰三角形三线合一)
O
D
B
C
A
法二:
菱 形
三角形
转化
辨析定义,强化性质
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
2.菱形具有而矩形不一定有的性质是( )
A.对角线互相平分 B.四条边相等
C.对角相等 D.邻角互补
D
B
在菱形ABCD中,边长是 10,
40
16
渐进变式,内化性质
例:
(1)求菱形的周长.
(2)若BD=12,求AC的长.
请先按暂停键!思考完成后
再按回播放键!
AC=16
在菱形ABCD中,
渐进变式,内化性质
例:
若BD=12,AC=16,求菱形的面积.
请先按暂停键!思考完成后
再按回播放键!
∴AC⊥BD
OB= OD= BD=6
解:∵四边形ABCD是菱形
∴S菱形ABCD=S△ACD+S△ABC
在菱形ABCD中,
渐进变式,内化性质
例:
请先按暂停键!思考完成后
再按回播放键!
a
b
S菱形ABCD=S△ACD+S△ABC
菱形的面积=底×高=对角线乘积的一半.
若BD= ,AC= ,求菱形的面积.
变式:
解:
在菱形ABCD中,边长是 10,
40
16
渐进变式,内化性质
例:
(1)求菱形的周长.
(2)若BD=12,求AC的长.
(3)若∠BAC = 30°,求AC的长.
请先按暂停键!思考完成后
再按回播放键!
解:∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
AC⊥BD(菱形的对角线互相垂直)
∵∠BAC=30°
∴∠BAD=60°
∴△ABD是等边三角形.
∴OB=OD=5
又由勾股定理,得AO=
AC=2AO=
渐进变式,内化性质
(3)若∠BAC= 30°,求AC的长.
在菱形ABCD中,边长是 10,
例:
纵观过去,指引未来
四边形
平行四边形
边特殊化
我们学行四边形、矩形,通过类比,学习菱形
定义
性质
定义
性质
边
角
对角线
对称性
判定
应用
角特殊化
菱形
矩形
定义
性质
边
角
对角线
对称性
判定
应用
边特殊化
同学们再见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
