浙教版八年级下册 5.1.2 矩形 课件(共16张PPT)
文档属性
| 名称 | 浙教版八年级下册 5.1.2 矩形 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
浙教版数学八年级下册第五单元第一节第二课时
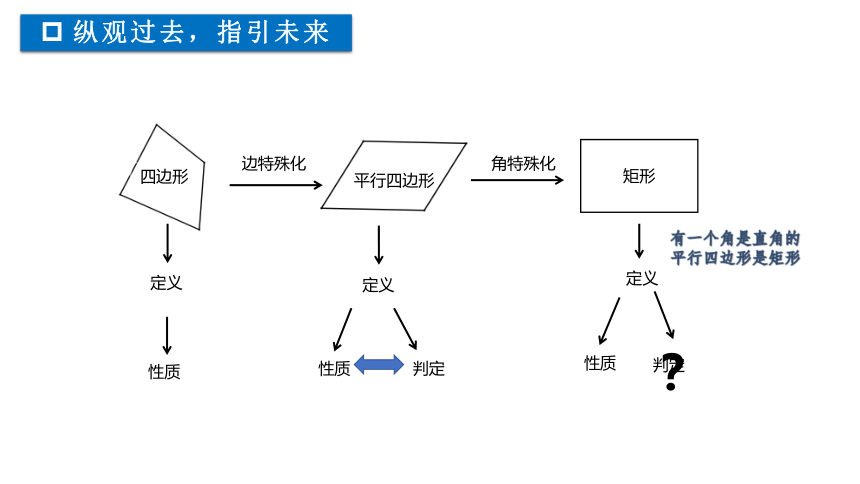
纵观过去,指引未来
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
?
判定
定义
定义
定义
深入探究,形成概念
B
C
D
A
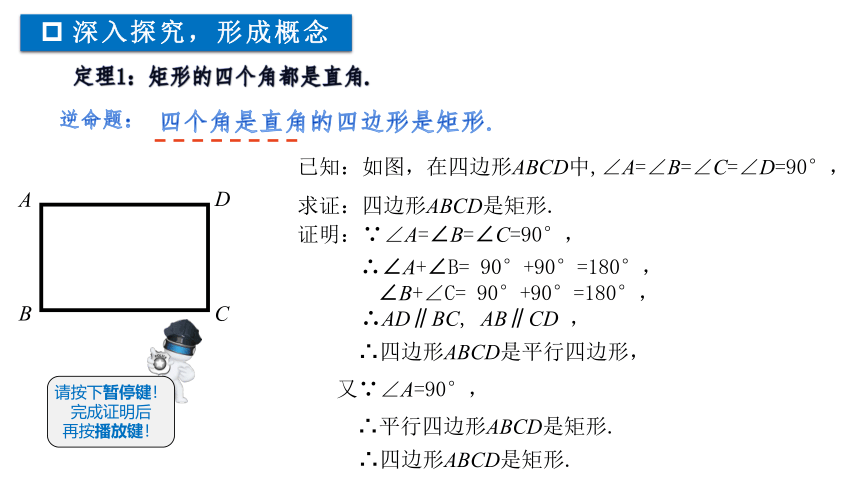
已知:如图,在四边形ABCD中,∠A=∠B=∠C=∠D=90°,求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴∠A+∠B= 90°+90°=180°,
∠B+∠C= 90°+90°=180°,
∴AD∥BC, AB∥CD ,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形.
请按下暂停键!完成证明后
再按播放键!
∴四边形ABCD是矩形.
深入探究,形成概念
B
C
D
A
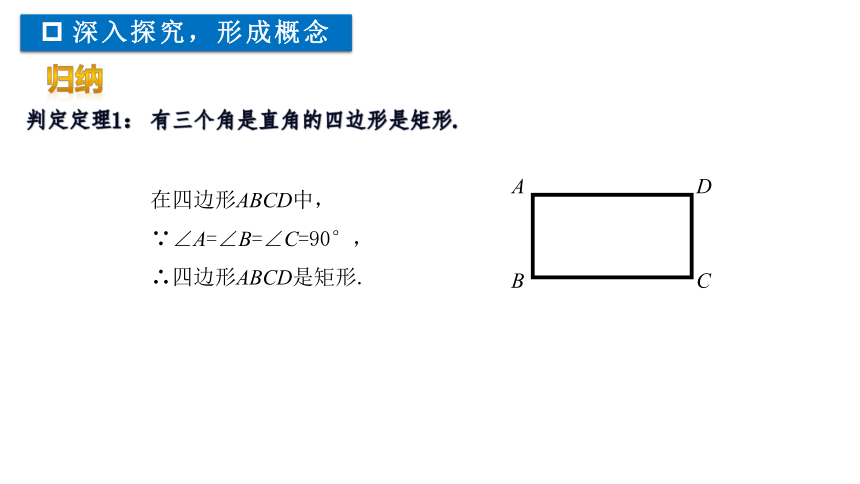
在四边形ABCD中,∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
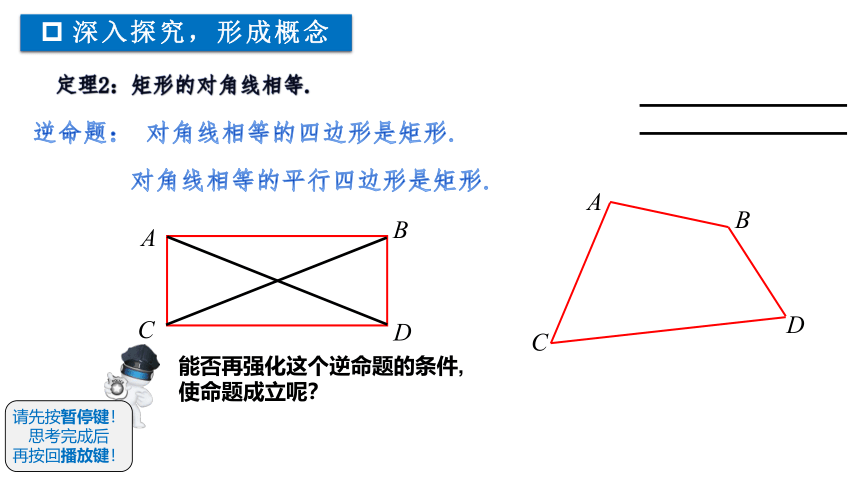
深入探究,形成概念
能否再强化这个逆命题的条件,使命题成立呢?
请先按暂停键!思考完成后
再按回播放键!
A
B
C
D
C
D
B
A
深入探究,形成概念
B
C
D
A
O
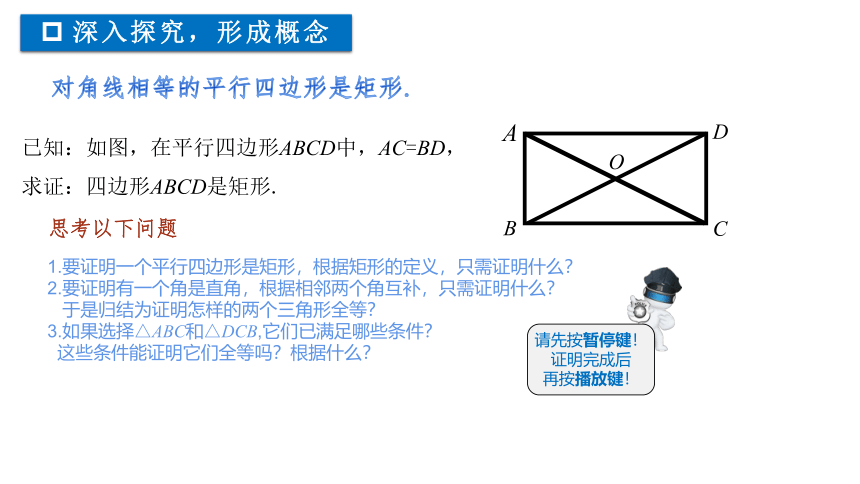
已知:如图,在平行四边形ABCD中,AC=BD,
求证:四边形ABCD是矩形.
1.要证明一个平行四边形是矩形,根据矩形的定义,只需证明什么?
2.要证明有一个角是直角,根据相邻两个角互补,只需证明什么?
于是归结为证明怎样的两个三角形全等?
3.如果选择△ABC和△DCB,它们已满足哪些条件?
这些条件能证明它们全等吗?根据什么?
思考以下问题
请先按暂停键!证明完成后
再按播放键!
深入探究,形成概念
B
C
D
A
O
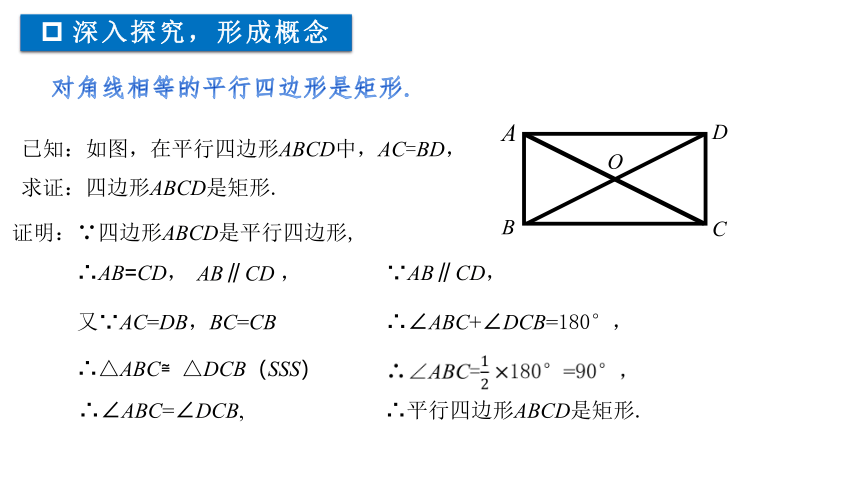
已知:如图,在平行四边形ABCD中,AC=BD,
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,
又∵AC=DB,BC=CB
∴△ABC≌△DCB(SSS)
∴∠ABC=∠DCB,
AB∥CD ,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴平行四边形ABCD是矩形.
深入探究,形成概念
在平行四边形ABCD中,
∵AC=BD,
∴平行四边形ABCD是矩形.
B
C
D
A
3.对角线相等的四边形是矩形
深入探究,形成概念
想一想:判断下列命题是否正确,并说明理由.
1.对角互补的平行四边形是矩形
2.一组邻角相等的平行四边形是矩形
4.内角都相等的四边形是矩形
四边形
√
√
√
×
请先按暂停键!思考完成后
再按回播放键!
有一个直角
对角线相等
有三个直角
例题演练,掌握新知
A
B
C
D
.
.
.
.
G
E
F
H
A
B
C
D
O
.
.
.
.
G
H
E
F
∠FGH=90°
∠GHE=90°
∠HEF=90°
例1:一张四边形纸板ABCD两条对角线互相垂直,若要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
解:分别取AB,BC,CD,DA的中点E,F,G,H,
依次连结EF,FG,GH,HE,
∵EF是△ABC的中位线,
∴EF∥AC,
∵AC⊥BD,
∴EF⊥BD,
∵EH是△ABD的中位线,
即∠HEF=90°,
同理∠EHG=90°,
∠HGF=90°,
∴ EF⊥EH,
∴四边形EFGH是矩形.
例题演练,掌握新知
A
B
C
D
O
E
F
G
H
.
.
.
.
请先按暂停键!思考完成后
再按回播放键!
∴EH∥BD,
深化拓展,体悟新知
例2:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.
证明:∵四边形ABEC是平行四边形,
∵BC是等腰三角形BED底边ED上的高,
∴EC=CD,
∴AB CD,
∴四边形ABCD是平行四边形.
∴ 平行四边形ABCD是矩形.
∠BCD=90°,
∵∠BCD=90°,
请先按暂停键!思考完成后
再按回播放键!
∴AB CE,
深化拓展,体悟新知
∵BC是等腰三角形BED底边ED上的高,
∴EC=CD,
∴AB CD,
∴四边形ABCD是平行四边形.
AC=BE,
BE=BD,
∵AC=BE,BE=BD,
∴BD=AC,
∴平行四边形ABCD是矩形.
可否用“三个角都是直角的四边形是矩形”来证明呢?
例2:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.
证明:∵四边形ABEC是平行四边形,
∴AB CE,
小结新课,梳理新知
数学思想方法:
类比
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
小结新课,梳理新知
两组对边相等
两组对边平行
一组对边平行且相等
对角线互相平分
转化
数学思想方法:
类比
四边形
有一个直角
对角线相等
有三个直角
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
同学们再见
浙教版数学八年级下册第五单元第一节第二课时
纵观过去,指引未来
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
?
判定
定义
定义
定义
深入探究,形成概念
B
C
D
A
已知:如图,在四边形ABCD中,∠A=∠B=∠C=∠D=90°,求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴∠A+∠B= 90°+90°=180°,
∠B+∠C= 90°+90°=180°,
∴AD∥BC, AB∥CD ,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形.
请按下暂停键!完成证明后
再按播放键!
∴四边形ABCD是矩形.
深入探究,形成概念
B
C
D
A
在四边形ABCD中,∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
深入探究,形成概念
能否再强化这个逆命题的条件,使命题成立呢?
请先按暂停键!思考完成后
再按回播放键!
A
B
C
D
C
D
B
A
深入探究,形成概念
B
C
D
A
O
已知:如图,在平行四边形ABCD中,AC=BD,
求证:四边形ABCD是矩形.
1.要证明一个平行四边形是矩形,根据矩形的定义,只需证明什么?
2.要证明有一个角是直角,根据相邻两个角互补,只需证明什么?
于是归结为证明怎样的两个三角形全等?
3.如果选择△ABC和△DCB,它们已满足哪些条件?
这些条件能证明它们全等吗?根据什么?
思考以下问题
请先按暂停键!证明完成后
再按播放键!
深入探究,形成概念
B
C
D
A
O
已知:如图,在平行四边形ABCD中,AC=BD,
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,
又∵AC=DB,BC=CB
∴△ABC≌△DCB(SSS)
∴∠ABC=∠DCB,
AB∥CD ,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴平行四边形ABCD是矩形.
深入探究,形成概念
在平行四边形ABCD中,
∵AC=BD,
∴平行四边形ABCD是矩形.
B
C
D
A
3.对角线相等的四边形是矩形
深入探究,形成概念
想一想:判断下列命题是否正确,并说明理由.
1.对角互补的平行四边形是矩形
2.一组邻角相等的平行四边形是矩形
4.内角都相等的四边形是矩形
四边形
√
√
√
×
请先按暂停键!思考完成后
再按回播放键!
有一个直角
对角线相等
有三个直角
例题演练,掌握新知
A
B
C
D
.
.
.
.
G
E
F
H
A
B
C
D
O
.
.
.
.
G
H
E
F
∠FGH=90°
∠GHE=90°
∠HEF=90°
例1:一张四边形纸板ABCD两条对角线互相垂直,若要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
解:分别取AB,BC,CD,DA的中点E,F,G,H,
依次连结EF,FG,GH,HE,
∵EF是△ABC的中位线,
∴EF∥AC,
∵AC⊥BD,
∴EF⊥BD,
∵EH是△ABD的中位线,
即∠HEF=90°,
同理∠EHG=90°,
∠HGF=90°,
∴ EF⊥EH,
∴四边形EFGH是矩形.
例题演练,掌握新知
A
B
C
D
O
E
F
G
H
.
.
.
.
请先按暂停键!思考完成后
再按回播放键!
∴EH∥BD,
深化拓展,体悟新知
例2:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.
证明:∵四边形ABEC是平行四边形,
∵BC是等腰三角形BED底边ED上的高,
∴EC=CD,
∴AB CD,
∴四边形ABCD是平行四边形.
∴ 平行四边形ABCD是矩形.
∠BCD=90°,
∵∠BCD=90°,
请先按暂停键!思考完成后
再按回播放键!
∴AB CE,
深化拓展,体悟新知
∵BC是等腰三角形BED底边ED上的高,
∴EC=CD,
∴AB CD,
∴四边形ABCD是平行四边形.
AC=BE,
BE=BD,
∵AC=BE,BE=BD,
∴BD=AC,
∴平行四边形ABCD是矩形.
可否用“三个角都是直角的四边形是矩形”来证明呢?
例2:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形.
证明:∵四边形ABEC是平行四边形,
∴AB CE,
小结新课,梳理新知
数学思想方法:
类比
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
小结新课,梳理新知
两组对边相等
两组对边平行
一组对边平行且相等
对角线互相平分
转化
数学思想方法:
类比
四边形
有一个直角
对角线相等
有三个直角
边特殊化
四边形
平行四边形
性质
性质
判定
角特殊化
矩形
性质
判定
定义
定义
定义
同学们再见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
