2022-2023学年浙教版九年级数学上册 1.4.3二次函数的应用 课件(共14张PPT)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册 1.4.3二次函数的应用 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
例1.如图,在△ABC 中,∠B=90°
,AB=6,
BC=8,D是AB 的中点。动点P从点B 开始沿边BA以1/s的速度移动,动点Q从点B开始沿边BC向C以2/s的速度移动(P,Q两点任意一点到达终点即停止运动).P关于D的对称点为P',如果四边形ACQP'的面积记为S,
二次函数的应用
例2:如图,B船位于A船正东26km处,现在A,B
两船同时出发,A船以12km/h的速度朝正北方向行
驶,B船以5km/h的速度朝正西方向行驶.何时两船
相距最近 最近距离是多少
A
B
A′
B′
设经过t时后,A、B两船分别到达A′、B′(如图),两船的距离为d(km)
任务二:
例3、如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).
(1)求抛物线的解析式;
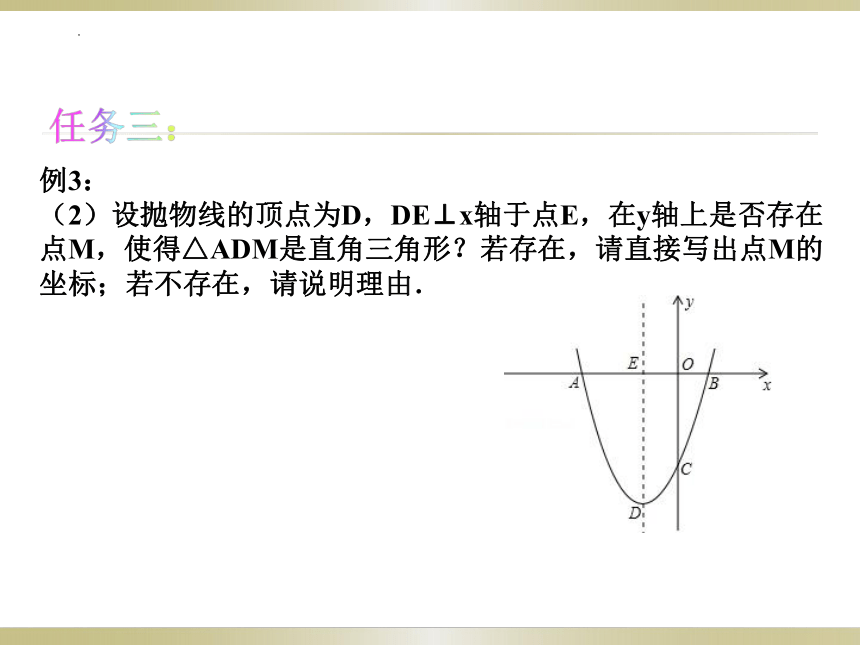
任务三:
例3:
(2)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
任务三:
例3.某饮料经营部每天的固定成本为200元,某销售的饮料每瓶进价为5元。
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
(1)若记销售单价比每瓶进价多x元时,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少?
例4.一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- 0.5 gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
例4
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
课内练习
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
40
50
30
20
10
x(m)
5
10
15
y(m)
⑶ 当球的高度为5m时,
球离抛出地面的水平
距离是多少m?
⑵ 求球被抛出多远;
利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
例5
1
2
0
-1
-2
x
1
2
3
4
5
6
y
在本节的例5中,我们把一元二次方程x +x-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动
利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
例5
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x
y=1-x
P31作业题T5
已知一个二次函数的图像与x轴的交点为(-2,0),(4,0),且顶点在函数y=2x的图像上.求这个二次函数的表达式.
当堂检测
1、教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-1 /12 (x-4)2+3,由此可知铅球推出的距离是______m.
2、如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7m,则DE的长为_____m.
例1.如图,在△ABC 中,∠B=90°
,AB=6,
BC=8,D是AB 的中点。动点P从点B 开始沿边BA以1/s的速度移动,动点Q从点B开始沿边BC向C以2/s的速度移动(P,Q两点任意一点到达终点即停止运动).P关于D的对称点为P',如果四边形ACQP'的面积记为S,
二次函数的应用
例2:如图,B船位于A船正东26km处,现在A,B
两船同时出发,A船以12km/h的速度朝正北方向行
驶,B船以5km/h的速度朝正西方向行驶.何时两船
相距最近 最近距离是多少
A
B
A′
B′
设经过t时后,A、B两船分别到达A′、B′(如图),两船的距离为d(km)
任务二:
例3、如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).
(1)求抛物线的解析式;
任务三:
例3:
(2)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
任务三:
例3.某饮料经营部每天的固定成本为200元,某销售的饮料每瓶进价为5元。
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
(1)若记销售单价比每瓶进价多x元时,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少?
例4.一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- 0.5 gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
例4
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
课内练习
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
40
50
30
20
10
x(m)
5
10
15
y(m)
⑶ 当球的高度为5m时,
球离抛出地面的水平
距离是多少m?
⑵ 求球被抛出多远;
利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
例5
1
2
0
-1
-2
x
1
2
3
4
5
6
y
在本节的例5中,我们把一元二次方程x +x-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动
利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
例5
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x
y=1-x
P31作业题T5
已知一个二次函数的图像与x轴的交点为(-2,0),(4,0),且顶点在函数y=2x的图像上.求这个二次函数的表达式.
当堂检测
1、教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-1 /12 (x-4)2+3,由此可知铅球推出的距离是______m.
2、如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7m,则DE的长为_____m.
同课章节目录
