2.6有理数的混合运算 课件(共15张PPT)
文档属性
| 名称 | 2.6有理数的混合运算 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1017.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.6有理数的混合运算
浙教版 七年级上册
教学目标
教学目标:
掌握有理数混合运算法则,并能进行有理数的混合运算的计算。
重点:有理数混合运算法则。
难点:培养探索思维方式。
新知导入
(1)3-(-2)+(-1)
(2)6÷3×(-2)
(3)(-2)4
请根据运算法则,写出具体的计算过程,说出计算步骤.
=3+2-1=4
=2×(-2)=-4
所有运算的步骤:
1、确定符号
2、计算数值部分
=24=16
新知讲解
一座圆形花坛的半径为3 m,中间雕塑的底面是边长为1.2 m的正方形(如图).
(1)你能用算式表示花坛的实际种花面积吗?
(2)这个算式有哪几种运算?
(3)应怎样计算?
(4)这个花坛的实际种花面积是多少?
3m
1.2m
(1) ;
(2)乘方、乘法、减法运算;
(3)先算乘方,再算乘法、最后算减法;
(4)这个花坛的实际种花面积是 .
新知讲解
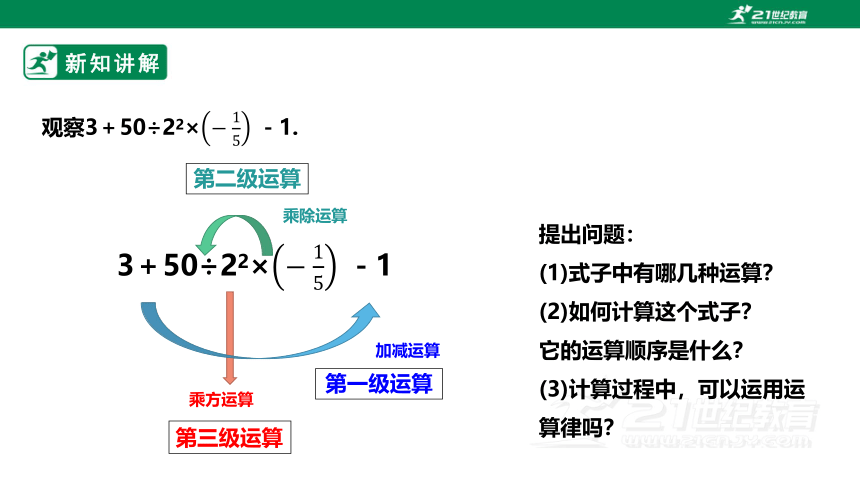
第一级运算
第三级运算
第二级运算
乘除运算
乘方运算
加减运算
提出问题:
(1)式子中有哪几种运算?
(2)如何计算这个式子?
它的运算顺序是什么?
(3)计算过程中,可以运用运算律吗?
观察3+50÷22× -1.
3+50÷22× -1
新知讲解
有理数混合运算的法则:
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
新知讲解
例1、计算:
(1) (2)
解:(1)
=36×
=6-8
=-2
(2)
=
=
=-
同级运算,从左至右
异级运算,由高到低
若有括号,先算内部
简便方法,优先采用
新知讲解
例2 底面半径为10cm,高为30cm的圆柱形水桶中装满了水。小明先将桶中的水倒满2个底面半径为3cm,高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别是50cm,20cm和20cm的长方体容器内。长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度不计)
新知讲解
解:水桶内水的体积为π×,倒满2个杯子后,剩下的水的体积为(π×)
(π×)÷(50×20)
=(9000-270)÷1000
=8730÷1000
=8.73(cm)
答:容器内水的高度约为8.73cm
课堂练习
1.下列各式的变形中,用错运算律的是( )
A.(3+4)+5=3+(4+5)
B.(3×4)×5=5×(3×4)
C.3×(4+5)=3×4+3×5
D.3÷(4+5)=3÷4+3÷5
D
课堂练习
2.设a=-2×32,b=(-2×3)2,c=-(2×3)2,那么a,b,c的大小关系是 ( )
A.a<c<b B.c<a<b C.c<b<a D.a<b<c
B
3.按照如图所示的操作步骤,若输入x的值为5,则输出的值为_____.
-10
课堂练习
4.计算:
(1)-10+8÷(-2)2-(-4)×(-3);
解:原式=-10+8÷4-12=-10+2-12=-20;
(2)4×(-3)2-5×(-2)3+6;
解:原式=4×9-5×(-8)+6=36+40+6=82;
课堂总结
有理数的混合运算
运算法则
运算策略
先算乘方,再算乘除,最后算加减
同级运算,按从左到右的顺序进行
有括号先进行括号内的运算,按小括号、中括号、大括号的顺序依次进行
根据算式特征,灵活选择运算律简便计算
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.6有理数的混合运算
浙教版 七年级上册
教学目标
教学目标:
掌握有理数混合运算法则,并能进行有理数的混合运算的计算。
重点:有理数混合运算法则。
难点:培养探索思维方式。
新知导入
(1)3-(-2)+(-1)
(2)6÷3×(-2)
(3)(-2)4
请根据运算法则,写出具体的计算过程,说出计算步骤.
=3+2-1=4
=2×(-2)=-4
所有运算的步骤:
1、确定符号
2、计算数值部分
=24=16
新知讲解
一座圆形花坛的半径为3 m,中间雕塑的底面是边长为1.2 m的正方形(如图).
(1)你能用算式表示花坛的实际种花面积吗?
(2)这个算式有哪几种运算?
(3)应怎样计算?
(4)这个花坛的实际种花面积是多少?
3m
1.2m
(1) ;
(2)乘方、乘法、减法运算;
(3)先算乘方,再算乘法、最后算减法;
(4)这个花坛的实际种花面积是 .
新知讲解
第一级运算
第三级运算
第二级运算
乘除运算
乘方运算
加减运算
提出问题:
(1)式子中有哪几种运算?
(2)如何计算这个式子?
它的运算顺序是什么?
(3)计算过程中,可以运用运算律吗?
观察3+50÷22× -1.
3+50÷22× -1
新知讲解
有理数混合运算的法则:
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
新知讲解
例1、计算:
(1) (2)
解:(1)
=36×
=6-8
=-2
(2)
=
=
=-
同级运算,从左至右
异级运算,由高到低
若有括号,先算内部
简便方法,优先采用
新知讲解
例2 底面半径为10cm,高为30cm的圆柱形水桶中装满了水。小明先将桶中的水倒满2个底面半径为3cm,高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别是50cm,20cm和20cm的长方体容器内。长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度不计)
新知讲解
解:水桶内水的体积为π×,倒满2个杯子后,剩下的水的体积为(π×)
(π×)÷(50×20)
=(9000-270)÷1000
=8730÷1000
=8.73(cm)
答:容器内水的高度约为8.73cm
课堂练习
1.下列各式的变形中,用错运算律的是( )
A.(3+4)+5=3+(4+5)
B.(3×4)×5=5×(3×4)
C.3×(4+5)=3×4+3×5
D.3÷(4+5)=3÷4+3÷5
D
课堂练习
2.设a=-2×32,b=(-2×3)2,c=-(2×3)2,那么a,b,c的大小关系是 ( )
A.a<c<b B.c<a<b C.c<b<a D.a<b<c
B
3.按照如图所示的操作步骤,若输入x的值为5,则输出的值为_____.
-10
课堂练习
4.计算:
(1)-10+8÷(-2)2-(-4)×(-3);
解:原式=-10+8÷4-12=-10+2-12=-20;
(2)4×(-3)2-5×(-2)3+6;
解:原式=4×9-5×(-8)+6=36+40+6=82;
课堂总结
有理数的混合运算
运算法则
运算策略
先算乘方,再算乘除,最后算加减
同级运算,按从左到右的顺序进行
有括号先进行括号内的运算,按小括号、中括号、大括号的顺序依次进行
根据算式特征,灵活选择运算律简便计算
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
