3.2实数 课件（共20张PPT）

(共20张PPT)
3.2实数
浙教版 七年级上册
教学目标
教学目标：
1. 从感性上认可无理数的存在，并通过探索说出无理数的特征，弄清有理数与无理数的本质区别。
2. 了解并掌握无理数、实数的概念以及实数的分类。
3. 知道实数与数轴上的点的一一对应关系。
重点：无理数、实数的意义，在数轴上表示实数。
难点：无理数与有理数的本质区别，实数与数轴上的点的一一对应关系。
新知导入
交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v＝16 ，其中v表示车速(单位：km/h)，d表示刹车后车轮滑过的距离(单位：m)，f 表示摩擦因数．在一次交通事故调查中，测得d＝20 m，
f＝1.2.肇事汽车v＝16× ＝16 .
对数 提出如下问题：
(1)可能是整数吗？
(2)可能是分数吗？
(3)如果既不是整数又不是分数，那么究竟是什么数呢？
新知讲解
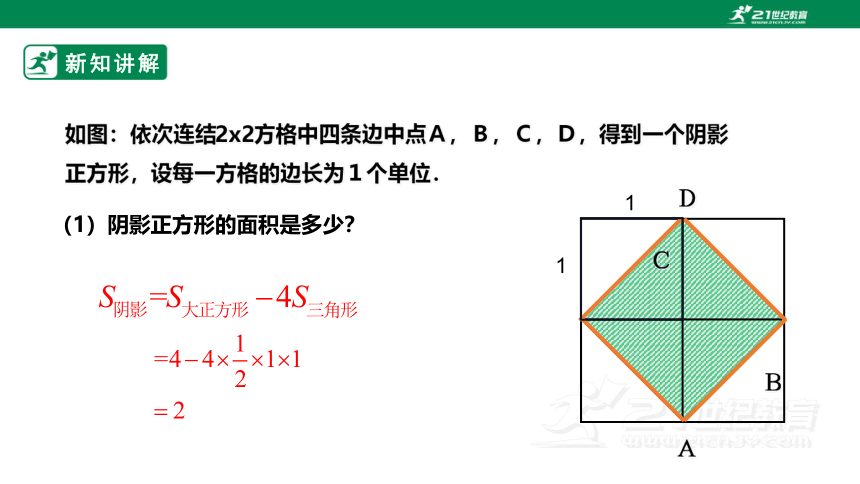
如图：依次连结2x2方格中四条边中点Ａ，Ｂ，Ｃ，Ｄ，得到一个阴影正方形，设每一方格的边长为１个单位．
（1）阴影正方形的面积是多少？
1
1
Ａ
Ｂ
Ｃ
Ｄ
1< <2
新知讲解
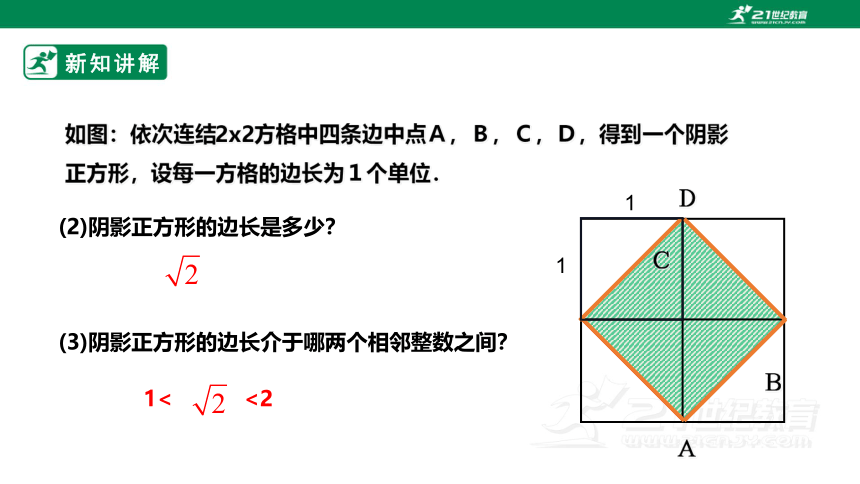
如图：依次连结2x2方格中四条边中点Ａ，Ｂ，Ｃ，Ｄ，得到一个阴影正方形，设每一方格的边长为１个单位．
1
1
Ａ
Ｂ
Ｃ
Ｄ
(2)阴影正方形的边长是多少？
(3)阴影正方形的边长介于哪两个相邻整数之间？
新知讲解
到底是一个什么样的数？
从“数”的角度：
归纳： 既不是整数，也不是分数，所以不是有理数.
探究：
不是
追问1： 可能是整数吗？
不是
追问2： 可能是分数吗？
新知讲解
∵1.42＝1.96， 1.52＝2.25
∵1.412＝1.9881，1.422＝2.0164
……
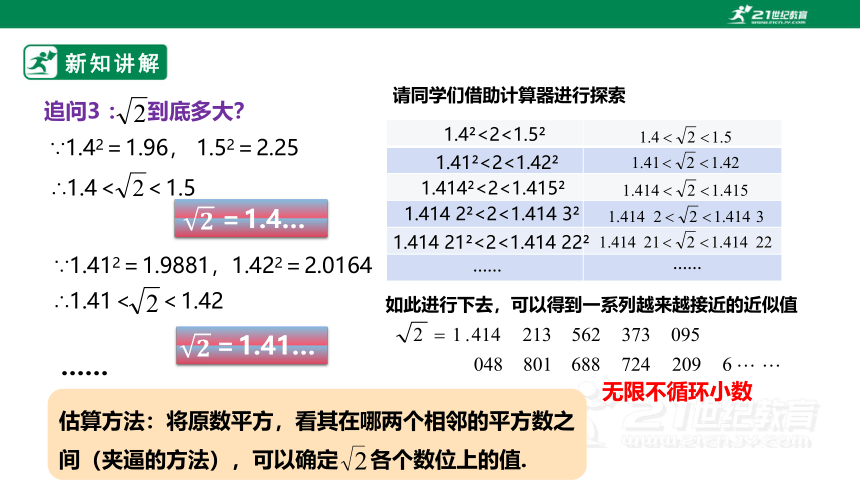
追问3 ： 到底多大？
∴1.4＜ ＜1.5
∴1.41＜ ＜1.42
请同学们借助计算器进行探索
1.4 <2<1.5
1.41 <2<1.42
1.414 <2<1.415
1.414 2 <2<1.414 3
1.414 21 <2<1.414 22
……
……
如此进行下去，可以得到一系列越来越接近的近似值
无限不循环小数
＝1.4…
＝1.41…
估算方法：将原数平方，看其在哪两个相邻的平方数之间（夹逼的方法），可以确定 各个数位上的值.
新知讲解
既不是有限小数，也不是无限循环小数（不能化为分数）
我们把这种无限不循环小数叫做无理数.
是无理数吗？2.020 020 002 000 02…是无理数吗？
＝ 1.570 796 326 794 89… ，2.020 020 002 000 02… ，
它们都是无限不循环小数，是无理数.
常见的一些无理数：
(1)含 π 的一些数；(2)开不尽方的数；
(3)有规律但不循环的小数，如1.01001000100001…
新知讲解
事实上，任何一个有理数都可以写成有限小数或无限循环小数.
反过来，任何有限小数或无限循环小数也都是有理数.
使用计算器计算，把下列有理数写成小数的形式，你有什么发现？
新知讲解
负有理数
实数的分类：
实数
有理数
无理数
正有理数
正有理数
有理数和无理数统称为实数
负有理数
无限不循环小数
零
有限小数和无限循环小数
新知讲解
把数从有理数扩充到实数以后，有理数中的相反数和绝对值的概念同样适用。
例如： 和 互为相反数
我们知道，每一个有理数都可以用数轴上的点表示出来，那么无理数可以在数轴上表示出来吗？
新知讲解
0
1
2
3
-1
-2
-3
以单位长度为边长画一个正方形，以原点为圆心，正方形的对角线为半径画弧.
弧与正半轴的交点就表示 ，
弧与负半轴的交点就表示 .
在实数范围内，每一个实数都可以用数轴上的点来表示；反过来，数轴上的每一个点都表示一个实数.我们说实数和数轴上的点是一一对应的.
有理数的大小比较法则也适用于实数：
在数轴上表示的两个实数，右边的数总比左边的数大.
新知讲解
例 把下列实数表示在数轴上，并比较它们的大小(用“<”连接)
，-π，1.5，-
解：把 ，-π，1.5，-表示在数轴上，如图
-3 -2 -1 0 1 2 3
-π
-
1.5
∴-π
课堂练习
1．判断下列说法是否正确：
（1）有限小数都是有理数； （ ）
（2）无限小数都是无理数； （ ）
（3）所有有理数都可以用数轴上的点表示，反过来，
数轴上的所有点都表示有理数； （ ）
（4）所有实数都可以用数轴上的点表示，反过来，
数轴上的所有点都表示实数． （ ）
√
×
×
√
课堂练习
2．下列说法正确的是（ ）
A．a一定是正实数 B． 是有理数
C． 是有理数 D．数轴上任一点都对应一个有理数
3．如图，表示 的点在数轴上哪两个字母之间（ ）
A．C与D B．A与B
C．A与C D．B与C
0
1
1.5
2
3
A
B
C
2.5
D
B
A
课堂练习
4．在数轴上画出表示 － －1 的点.
解：以单位长度为边长画一个正方形如图，以 －1 为圆心，正方形的对角线为半径画弧，与负半轴的交点就表示点－ －1.
0
-1
-2
-3
1
-4
－ －1
课堂练习
5.已知 是整数,求正整数n 的最大值和最小值.
解:∵ 是整数,
∴13-n≥0,
∴n≤13,
∴正整数n的最大值为13,最小值为4.
课堂总结
正有理数
负有理数
零
有理数
正无理数
负无理数
特殊
有限小数和无限循环小数
无限不循环小数
无理数
实数
数轴
的存在
的大小
0
正实数
负实数
数形结合
用有理数逼近无理数
一
一对应
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin