1.5全等三角形判定SSS

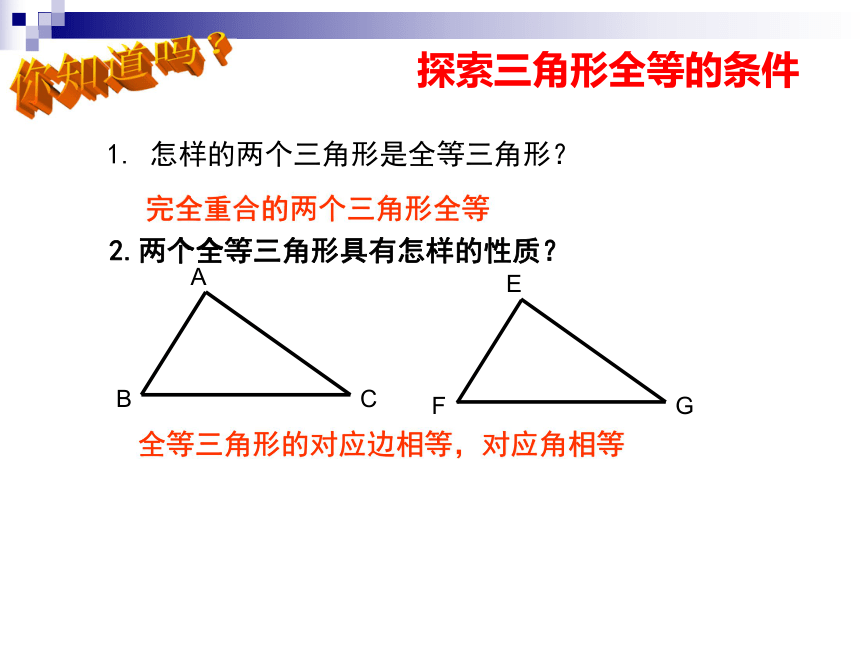
课件26张PPT。1.5 三角形全等的判定1. 怎样的两个三角形是全等三角形？2.两个全等三角形具有怎样的性质？探索三角形全等的条件 全等三角形的对应边相等，对应角相等完全重合的两个三角形全等你知道吗？已知三条线段长度分别为10cm，15cm，20cm，这三条线段能否组成一个三角形？1. 画线段AB=10cm.画法:2. 分别以A,B为圆心,15cm,20cm长为
半径 画两条圆弧,交于点C.3. 连结CA,AB.你能画出这个三角形吗？请你用刻度尺和圆规画一个三角形，使得这个三角形的三边是7cm、4cm、5cm 与同伴比一比，发现什么？
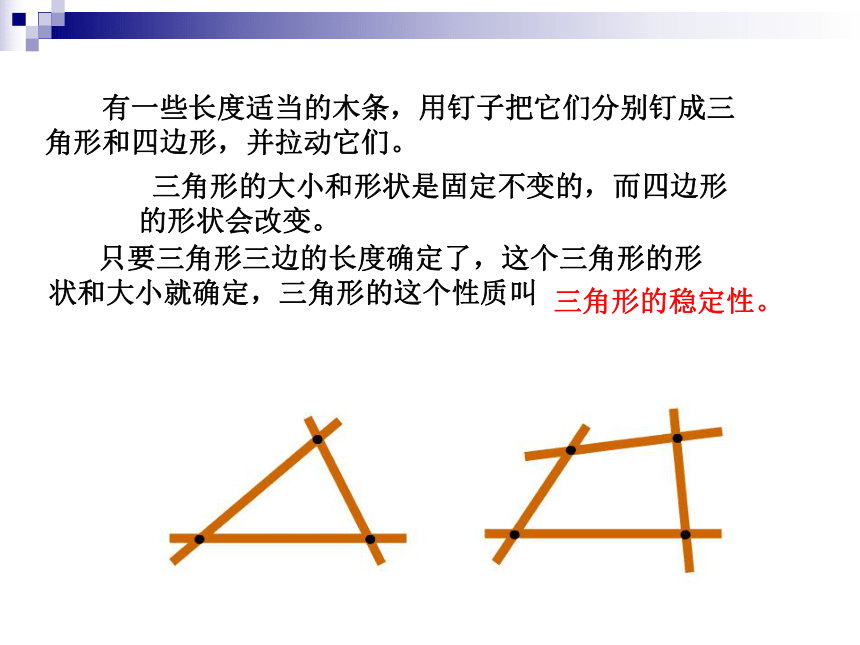
三角形全等的条件一 有三条边对应相等的两个三角形全等记做“边边边”或“SSS” 有一些长度适当的木条，用钉子把它们分别钉成三角形和四边形，并拉动它们。 三角形的大小和形状是固定不变的，而四边形
的形状会改变。 只要三角形三边的长度确定了，这个三角形的形
状和大小就确定，三角形的这个性质叫三角形的稳定性。 欣赏生活中的三角形例1已知：如图， 在四边形ABCD中，AB＝CD，AD＝CB，求证：∠B＝∠D证明：在△ABC和△CDA中
AB=CD（已知）
AD=CB（已知）
AC=CA（公共边）
∴△ABC≌△CDA（SSS）
∴∠B=∠D（全等三角形对应角相等）DACB2、如图，已知AB=AC,BD=CD,那么
ΔABD≌ΔACD吗?为什么?
∠BAD=∠CAD吗?为什么?那么AD平分∠BAC吗?
你能否得出不用量角器
画角的平分线的方法?已知一个角∠ BAC，请按以下画法用没有刻度的直尺和圆规画它的角平分线:
画法：1.以A为圆心，适当长为半径画圆弧，与角的两边分别交于E、F两点
2.分别以E、F为圆心，大于 EF长为半径画圆弧， 两条圆弧交于∠BAC内一点D
3.过点A，D做射线ADABC 1.已知AC=FE，BC=DE，AD=BF,
求证：△ABC ≌△ FDE基础练习： 2.如图，AB=AC，AE=AD，BD=CE，求证：△AEB ≌ △ ADC。CABDE基础练习：1.如图,已知AC =BD, CE=DF, AE=BF,则AE∥BF吗?∴ ΔACE≌ΔBDF(SSS)证明:
在ΔACE和ΔBDF中AC=BD(已知) CE=DF (已知) AE=BF (已知) ∴∠A=∠DBF(全等三角形的对应角相等) ∴ AE∥BF(同位角相等,两直线平行)提高训练2.如图，在四边形ABCD,AB=CD,AD=CB,DABC你能说明AB∥CD，AD∥BC吗？提高训练4、如图,在四边形ABCD中,AB=AD,CB=CD.你能通过添加辅助线,把它分成两个全等三角形吗?若能,画出辅助线,并给出证明.
ABCD已知：AB=AC,BD=CD
求证：∠B=∠C自主合作探究互动2、如图，小明在做数学作业时，遇到这样一个问题：
AB=CD，BC=AD，请说明∠A=∠C的道理。小明
动手测量了一下，发现∠A确实与∠C相等，但他
不能说明其中的道理，你能帮助他吗？ACBOD自主合作探究互动备选练习1.如图，已知AB=AC，BD=CD，则图中对应相等的角有（ ）
A、1对 B、2对 C、3对 D、4对知识回顾1. 已知三边长画三角形的方法.2. 三角形全等条件一.3. 三角形的稳定性.4. 角平分线的尺规作图法.作业